Достоинства и недостатки аналитического и табличного методов генерации случайных чисел

1. Оба метода реализуются сравнительно несложными программными процедурами.

2. Аналитический метод не имеет методической ошибки, но в полученные с его помощью формулы входят процедуры, требующие определенных затрат машинного времени. Этот недостаток в связи со стремительным ростом быстродействия ЭВМ становится все менее существенным. Некоторые функции вычисляются разложением в ряды, а ввиду того, что нельзя взять бесконечное количество членов ряда, такой подход приводит к ошибкам.

3. Табличные методы начинают терять свои позиции и, в частности, из-за того, что для их применения требуется составление таблиц и выделение памяти для их хранения. В принципе, повышения достоверности табличных методов можно достичь увеличением количества интервалов в таблице, но при этом увеличивается время поиска нужного интервала и требуемый объем памяти для хранения таблиц.

47. Как наиболее просто сгенерировать случайные числа, распределённые по гиперэкспоненциальному и эрланговскому закону?

Д ля некоторых законов, особенно составных, можно для генерации случайных чисел составить сравнительно несложные программы. Например, для генерации случайных чисел по эрланговскому закону, состоящему в общем случае из k экспоненциальных фаз, представленному на рис..

Для этого можно сгенерировать k случайных чисел, распределенных по экспоненциальному закону, каждое со своим m_i, , и сложить их. Получаем случайное число, распределенное по закону Эрланга.

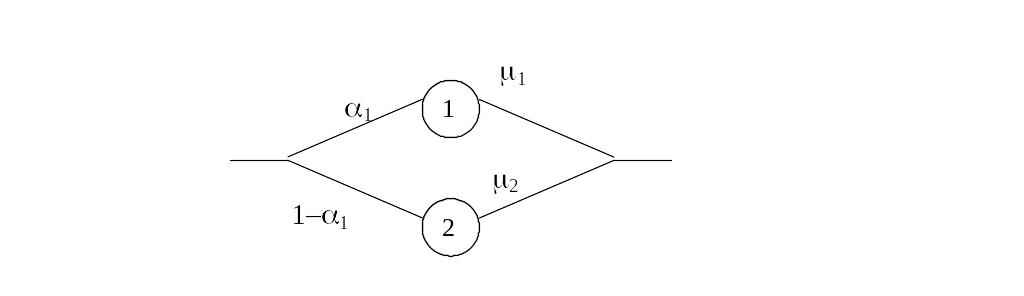
Для генерации гиперэкспоненциальных чисел, например состоящих из двух ветвей (рис. 3.11), требуется сгенерировать два равномерно распределенных случайных числа. Первое из них используется для выбора ветви, а второе для генерации случайного числа, распределенного экспоненциально с интенсивностью выбранной ветви.

Качество случайных чисел, сгенерированных по любым статистическим законам, рекомендуется оценивать по критериям согласия Пирсона и Колмогорова.

48. Какие методы оценки пригодности программной имитационной модели Вы знаете? Как можно оценить значимость результатов имитационного моделирования?

1. Оценка адекватности результатов имитационного моделирования и результатов аналитического моделирования или результатов, полученных на натурном объекте.

2. Оценка устойчивости результатов имитационного моделирования.

3. Оценка значимости зависимости результатов имитационного моделирования от используемых в модели факторов.

Оценка адекватности модели

Оценка адекватности результатов имитационного моделирования естественно может быть проведена только в случаях, когда имеются либо результаты аналитического моделирования, либо результаты, полученные на натурном объекте. Наиболее часто проводят сравнение средних значений методом построения доверительных интервалов. Так как средние значения при имитационном моделировании находятся сложением достаточно большого количества случайных чисел, то для их представления можно использовать нормальный закон на основании центральной предельной теоремы теории вероятностей. Центральная предельная теорема утверждает, что сумма достаточно большого количества случайных чисел, выработанных при достаточно общих условиях, подчинена нормальному закону вне зависимости от того, какому закону подчинены сами случайные числа, при этом , а . 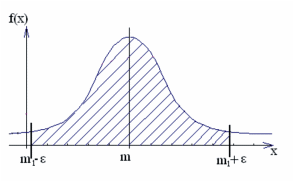Поэтому для оценок математических ожиданий, вычисляемых на основе суммирования случайных чисел, можно построить доверительный интервал на основании нормального закона