Расшифруйте следующие классификаторы смо: м/м/1; м/н2/1; е4/м/1; м/м/ m/к. В скольких состояниях могут находиться смо с классификатором м/м/ m/к? Модель м/м/1
Простейшая система массового обслуживания. Структурная схема системы
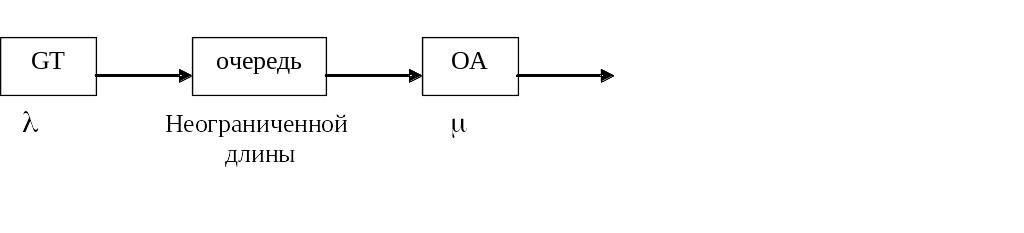
параметры: – интенсивность поступления транзактов; – интенсивность обслуживания.
В данной СМО может существовать стационарный режим, если ρ = λ/μ 1, что соответствует режиму, в котором интенсивность обслуживания не меньше интенсивности поступления транзактов в систему.
Модель м/м/1/3
В данной СМО ограничено количество транзактов в системе вследствие ограниченного количества мест в очереди k. Важнейшей характеристикой системы является вероятность отказа Ротк = Рk+1 (в СМО находится k + 1=3+1=4 транзакт). Кроме того, вычисляется относительная пропускная способность, которая является вероятностью, что поступающие транзакты будут обслужены q = 1 – Pотк. А также абсолютная пропускная способность, которая определяет количество обслуженных транзактов за единицу времени А = *q. Структурная схема данной СМО
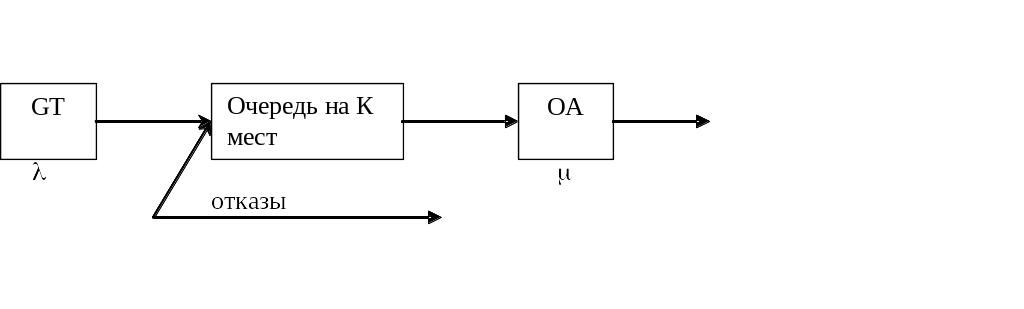
Граф-схема
изменения состояния СМО М/М/1/3
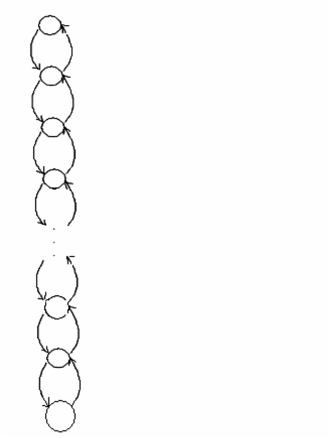
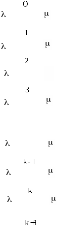
Для систем с отказами стационарный режим реализуется при любых значениях и , так как все «мешающие» этому транзакты будут удаляться из СМО без обслуживания.
Модель м/м/3
Структурная схема системы массового обслуживания с экспоненциальным входным потоком и обслуживанием и с количеством обслуживающих аппаратов, равным m.
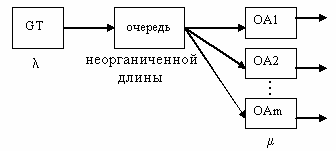
Рис. 17.15. Граф-схема изменения
состояния
СМО М/М/m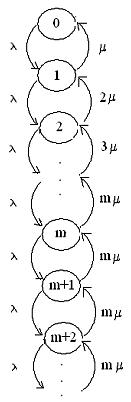
Стационарный
режим в данной системе может существовать,
если
.
Какие методы генерации равномерно распределённых случайных чисел Вы знаете? Чем отличаются псевдослучайные числа от случайных? Какие виды тестов используются для оценки качества равномерно распределённых случайных чисел?
Для генерации случайных чисел по заданному закону используют аналитические, табличные и специальные методы, основанные на функциональных особенностях генерируемых законов. В качестве задающих генераторов для реализации любых законов применяют генераторы равномерно распределенных случайных чисел. На практике наиболее часто применяют следующие четыре метода генерации случайных чисел:
1. Метод квадратов:
.
(3.1)
При возведении в квадрат n-разрядного числа в общем случае максимально в произведении будет 2n разряда. В качестве i-го случайного числа берется n средних разрядов предыдущего случайного числа.
2. Метод произведений:
.
(3.2)
Берется n средних разрядов произведения двух предыдущих чисел.
3. Конгруэнтный метод:
.
(3.3)
Символ º обозначает сравнимость по модулю. l и m – целые положительные числа. Для получения очередного случайного числа предыдущее умножается на l и затем делится на m, а остаток от деления берется в качестве i-го случайного числа.
4. Смешанный конгруэнтный метод. Улучшает качество случайных чисел и отличается от предыдущего добавлением к произведению целого положительного числаm
(3.4)
Генераторы псевдослучайных чисел современных ЭВМ, как правило, строятся на основании смешанного конгруэнтного метода. Качество случайных чисел, в том числе длина периода, которая является существенным показателем качества, во многом зависит от выбранных значений l, m, m.
Равномерный закон является самым простым для реализации. Как правило, для генерации случайных чисел по всем другим статистическим законам равномерный закон используется в качестве задающего генератора.
В вычислительных машинах большее распространение получили программные методы генерации случайных чисел, которые вычисляются по формуле, и поэтому в принципиальном плане не могут являться случайными. Они называются псевдослучайными.
Отличие псевдослучайных чисел от случайных заключается в том, что, начиная с некоторого времени, в них наблюдается периодичность, т.е. повторение одних и тех же случайных чисел, и это естественно, так как они вычисляются по формуле. В чисто случайных числах этого быть не может, так как является исключительно маловероятным событием. Это существенный недостаток псевдослучайных чисел, а их достоинством является возможность повторения одних и тех же последовательностей случайных чисел, т.е. если задавать одно и то же исходное число для генератора, то генератор каждый раз будет выдавать одни и те же последовательности чисел, что очень важно при проведении имитационного моделирования.
Проверка качества равномерно распределенных случайных чисел
Для проверки качества последовательности равномерно распределенных случайных чисел используют три вида тестов: на равномерность, случайность, периодичность.
Проверка равномерности
Наиболее часто используют два теста: частот и разрядов. Оценку производят по критерию согласия 2 (КС Пирсона).