37. Приведите характерные особенности равномерного закона.!!!!!!!!!!!!!!!!!!!!!!!!!!! Метод моментов для равномерного закона

Функция плотности равномерного закона: .

Вычислим первый и второй начальные моменты:

Вычислим стандартное отклонение и параметры равномерного закона:

Вычислим вероятность попадания случайной величины в интервалы гистограммы и гипотетическую ФР:

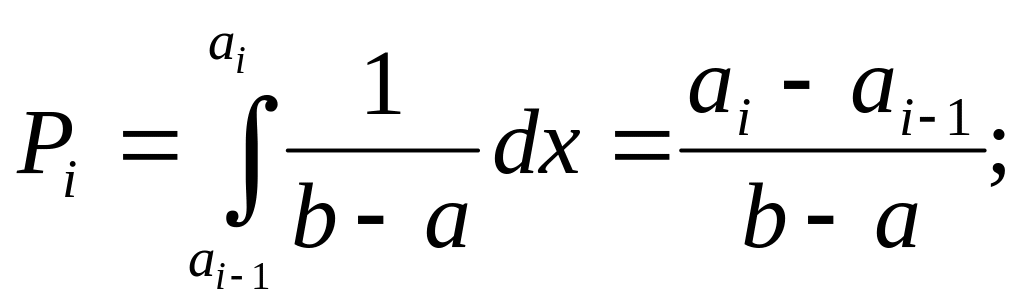
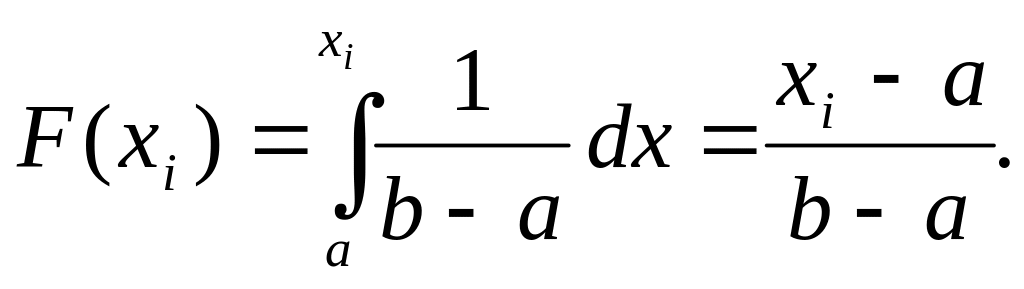
Следует учитывать, что при построении гистограммы принимается:

; .

38. Назовите три замечательных свойства экспоненциального закона, позволяющие строить марковские цепи.

В теории массового обслуживания центральное место занимает экспоненциальный закон благодаря своим следующим замечательным свойствам.

1. Ординарность.

Заключается в том, что если в ОМ действует несколько экспоненциальных законов, то в любой момент времени в такой системе не может произойти более одного события.

2. Стационарность (независимость от времени).

Стационарный режим в простейшей системе наступает тогда, когда выполняется условие, что интенсивность поступления транзактов l не превышает интенсивности их обслуживания m. В таких системах через некоторое время, которое называют переходным режимом, процесс изменения состояния системы перестает зависеть от времени и зависит только от технических характеристик ОМ и параметров внешней среды, в которой он функционирует. Условие наличия стационарного режима для простейшей СМО .

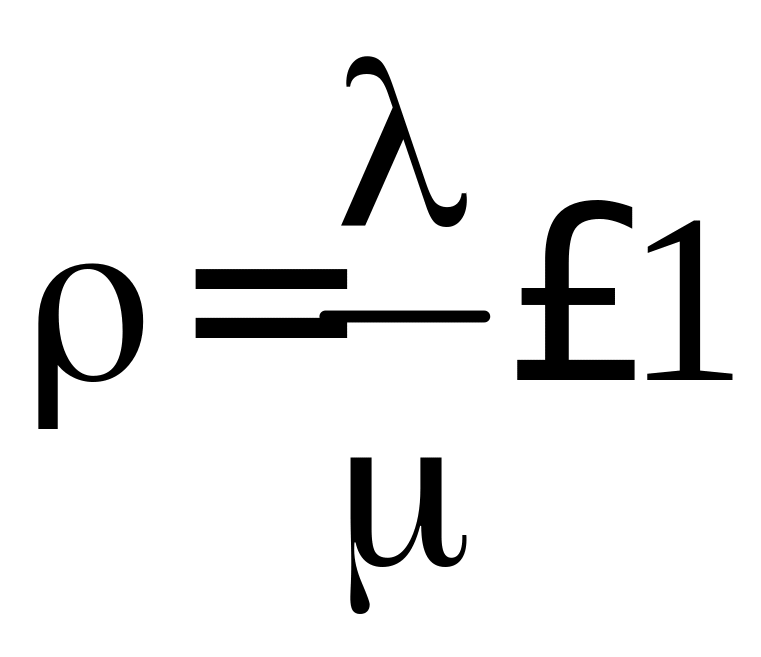3. Отсутствие последействия.

Заключается в том, что вероятность любого события в будущем не зависит от предыстории, в частности, вероятность, что система выйдет из какого-либо состояния в течения времени t, не должна зависеть от того, сколько времени система уже находилась в этом состоянии.

Эти три свойства позволяют строить марковские цепи, являющиеся основой аналитического моделирования СМО.

39. Назовите особенности гиперэкспоненциального и специального эрланговского законов. В каких случаях рекомендуется использовать гиперэкспоненциальный закон распределения случайных чисел, и в каких случаях специальный эрланговский?

Экспоненциальный закон является основным законом для создания моделей систем.

Недостаток экспоненциального закона – сравнительно небольшая область существования, что ограничивает его использование. Зависимость среднего квадратического отклонения от математического ожидания представляется прямой линией. Этот недостаток особенно существенен для разработки аналитических моделей.

σ

σ=m₁

m₁

Рис. Область существования экспоненциального закона распределения случайных чисел

Реальные экспериментальные распределения могут иметь самые различные значения m₁ и σ и для их представления с возможностью создания аналитических моделей применяют так называемые составные экспоненциальные распределения, которые представляют собой параллельные или последовательные совокупности различных экспоненциальных распределений.

Для случая, когда используют гиперэкспоненциальные распределения. Для случая когда используют эрланговские распределения.

Структурная схема гиперэкспоненциального закона распределения, состоящего из n ветвей, представлена на рис.

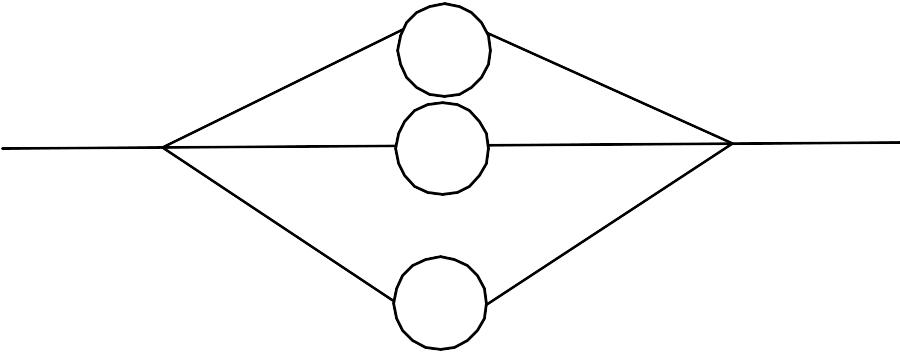
Достоинством представления случайных процессов гиперэкспоненциальными законами является возможность создания аналитических моделей систем, а явный недостаток по сравнению с представлением экспоненциальным законом заключается в сравнительно большом количестве параметров, которое требуется определить, т.е. при количестве ветвей n количество определяемых параметров 2n. Таким образом, требуется вычислить по МПФ не только 2n – 1 производных, но и решить систему, состоящую из 2n уравнений. Первое уравнение записывается из условия, что сумма вероятностей выбора ветвей должна равняться 1.

a₁ + a₂ + … + a_n = 1

Для упрощения аппроксимации на практике широко используется частный случай гиперэкспоненциального распределения, состоящего из двух ветвей, определяемого двумя параметрами. Использование гиперэкспоненциального закона расширяет возможности экспоненциального закона, распространяя область его применения выше линии экспоненциального закона.

Специальное эрланговское распределение (СЭР) состоит из k последовательно соединенных фаз, в каждой из которых распределение случайных величин подчиняется экспоненциальному закону с одинаковой интенсивностью mk. Структурная схема специального эрланговского закона распределения:

Ценность такого представления в том, что закон определяется всего двумя параметрами, и, следовательно, по МПФ требуется вычислить только две производные и решить полученную систему уравнений.