
- •Основные элементы матстатистики
- •§32. Вариационный и статистический ряд
- •§33. Выборочные характеристики вариационного ряда
- •§34. Доверительный интервал
- •§35. Выборочный коэффициент корреляции
- •§36. Ранговая корреляция
- •§37. Статистические гипотезы
- •§38. Критерии Пирсона и Стьюдента
- •Алгоритм применения -критерия Стьюдента для сравнения оценки средних величин двух выборок
- •§19. Нормальный закон распределения
§38. Критерии Пирсона и Стьюдента
Рассмотрим нормальные независимые
случайные величины
![]() ,
причем
,
причем
![]() ,
a
,
a
![]() .
Тогда сумма квадратов этих величин
.
Тогда сумма квадратов этих величин
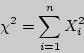
распределена по закону
![]() с
с
![]() степенями
свободы. С увеличением числа степеней
свободы распределение медленно
приближается к нормальному.
степенями
свободы. С увеличением числа степеней
свободы распределение медленно
приближается к нормальному.
1. Проверка гипотезы о расхождении
между эмпирическими (экспериментальными)
частотами
![]() и
теоретическими (контрольными) частотами
и
теоретическими (контрольными) частотами
![]() .
.
Алгоритм применения критерия Пирсона для сопоставления эмпирического и теоретического (другого эмпирического) распределений одного признака
Занести в таблицу наименование разрядов и эмпирические частоты (данные по экспериментальной группе).
Во 2-й столбец записать теоретические частоты (данные по контрольной группе).
Проверить равенство сумм частот
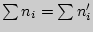 (или
их уравнять).
(или
их уравнять).
Подсчитать разности между эмпирическими и теоретическими частотами (экспериментальной и контрольной группами) по каждой строке и записать их в 3-й столбец.
Возвести в квадрат полученные разности и записать их в 4-й столбец.
Разделить полученные квадраты разностей на теоретические частоты (данные по контрольной группе) и записать в 5-й столбец.
Просуммировать значения 5-го столбца, обозначив ее
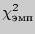
Определить по таблице критическое значение для соответствующего уровня значимости и данного числа степеней свободы
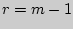 (
(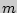 - количество разрядов признака, т.е.
строк в таблице).
- количество разрядов признака, т.е.
строк в таблице).
Если
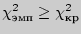 ,
то расхождения между распределениями
существенны на данном уровне значимости.
,
то расхождения между распределениями
существенны на данном уровне значимости.
2. Проверка гипотезы о нормальном
распределении генеральной совокупности.
Для того, чтобы свести задачу к указанному
в предыдущем пункте алгоритму, вычислим
выборочные среднюю
и
среднее квадратическое отклонение
![]() ,
а затем - теоретические частоты
,
а затем - теоретические частоты
![]() ,
где
-
объем выборки,
,
где
-
объем выборки,
![]() -
шаг (разность между двумя соседними
вариантами),
-
шаг (разность между двумя соседними
вариантами),
![]() ,
,
![]() (приложение
1)
(приложение
1)
Пусть
![]() -
нормальная случайная величина, причем
-
нормальная случайная величина, причем
![]() ,
,
![]() ,
a
,
a
![]() -
независимая от
величина,
которая распределена по закону
с
степенями
свободы. Тогда величина
-
независимая от
величина,
которая распределена по закону
с
степенями
свободы. Тогда величина
![]()
имеет распределение, которое называют -pаспределением или распределением Стьюдента (псевдоним английского статистика В. Госсета), с степенями свободы. С возрастанием числа степеней свободы распределение Стьюдента быстро приближается к нормальному.
Алгоритм применения -критерия Стьюдента для сравнения оценки средних величин двух выборок
Записать вариационный ряд результатов экспериментальной группы.
Записать вариационный ряд результатов контрольной группы.
Найти выборочные средние двух выборок
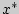 и
.
и
.
Найти выборочные дисперсии
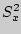 и
и
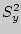 .
.
Вычислить эмпирическое значение критической статистики
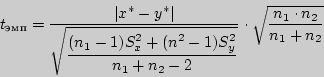
Определить по таблице критическое
значение
![]() для
соответствующего уровня значимости
и
данного числа степеней свободы
для
соответствующего уровня значимости
и
данного числа степеней свободы
![]() .
.
Если
![]() ,
то различия между средними значениями
экспериментальной и контрольной групп
существенны на данном уровне значимости.
,
то различия между средними значениями
экспериментальной и контрольной групп
существенны на данном уровне значимости.
3. Сравнение двух средних нормальных
генеральных совокупностей. Для того,
чтобы при заданном уровне значимости
проверить
нулевую гипотезу
![]() с
неизвестными, но одинаковыми дисперсиями
(в случае независимых малых выборок)
при конкурирующей гипотезе
с
неизвестными, но одинаковыми дисперсиями
(в случае независимых малых выборок)
при конкурирующей гипотезе
![]() ,
надо вычислить наблюдаемое значение
критерия:
,
надо вычислить наблюдаемое значение
критерия:
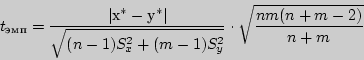
и по таблице критических точек
распределения Стьюдента по заданному
уровню значимости
и
числу степеней свободы
![]() найти
критическую точку
найти
критическую точку
![]() .
.
4. Проверка гипотезы о значимости
выборочного коэффициента корреляции.
Для того, чтобы при данном уровне
значимости
проверить
нулевую гипотезу
![]() o
равенстве нулю генерального коэффициента
корреляции нормальной двумерной
случайной величины при конкурирующей
гипотезе
o
равенстве нулю генерального коэффициента
корреляции нормальной двумерной
случайной величины при конкурирующей
гипотезе
![]() ,
надо вычислить наблюдаемое значение
критерия:
,
надо вычислить наблюдаемое значение
критерия:
![]()
и по таблице критических точек
распределения Стьюдента по заданному
уровню значимости
и
числу степеней свободы
![]() найти
критическую точку
.
найти
критическую точку
.
