
- •Основные элементы матстатистики
- •§32. Вариационный и статистический ряд
- •§33. Выборочные характеристики вариационного ряда
- •§34. Доверительный интервал
- •§35. Выборочный коэффициент корреляции
- •§36. Ранговая корреляция
- •§37. Статистические гипотезы
- •§38. Критерии Пирсона и Стьюдента
- •Алгоритм применения -критерия Стьюдента для сравнения оценки средних величин двух выборок
- •§19. Нормальный закон распределения
Основные элементы матстатистики
Термин статистика происходит от латинского слова "status" - состояние. В настоящее время статистика включает в себя следующие три раздела:
• сбор статистических сведений каких-либо массовых совокупностей;
• статистическое исследование полученных данных, выяснение закономерностей, которые могут быть установлены на основе данных массового наблюдения;
• разработка приемов статистического наблюдения и анализа статистических данных.
Последний раздел и составляет содержание математической статистики.
Совокупность значений какого-то признака объекта называется генеральной совокупностью, а основной задачей математической статистики является выяснение вероятностных свойств генеральной совокупности (распределение, числовые характеристики и т.д.). Полное исследование генеральной совокупности практически невозможно, поэтому обычно рассматривают только некоторые ее объекты, т.е. делают выборку, с помощью которой по вероятностным свойствам оценивают генеральную совокупность.
§32. Вариационный и статистический ряд
В математической статистике исследуются утверждения, которые могут быть сделаны на основе измерения некоторой величины, на простейшем примере поясним постановку (одной из многих) задач математической статистики.
Пусть требуется измерить некоторую
величину
![]() .
Результаты измерений
.
Результаты измерений
![]()
естественно рассматривать как значения
случайных величин
![]() ,
полученных в данном эксперименте. Если
измерительный инструмент не имеет
систематической ошибки, то можно положить
,
полученных в данном эксперименте. Если
измерительный инструмент не имеет
систематической ошибки, то можно положить
![]() .
Следовательно, возникает задача оценить
параметр
.
Для решения задачи рассмотрим случайную
величину
.
Следовательно, возникает задача оценить
параметр
.
Для решения задачи рассмотрим случайную
величину
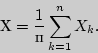
Тогда
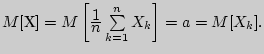
Это обстоятельство приводит к мысли построить статистические характеристики:
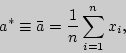

Первая представляет среднее арифметическое
наблюденных значений случайной величины
![]() и
статистическую дисперсию - во втором
случае. В соответствии с законом больших
чисел эти среднеарифметические сходятся
по вероятности соответственно к
математическому ожиданию величины
и
статистическую дисперсию - во втором
случае. В соответствии с законом больших
чисел эти среднеарифметические сходятся
по вероятности соответственно к
математическому ожиданию величины
![]() и
к дисперсии
и
к дисперсии
![]()
При ограниченности наблюдений эксперимента
заменой
![]() и
и
![]() на
на
![]() и
и
![]() совершаем
погрешность, а при небольшом числе
наблюдений величины
,
являются
случайными величинами. Возникает задача
об оценке неизвестных параметров
,
совершаем
погрешность, а при небольшом числе
наблюдений величины
,
являются
случайными величинами. Возникает задача
об оценке неизвестных параметров
,
![]() случайной
величины
случайной
величины
![]() на
основе экспериментальных данных, т.е.
задача - найти подходящие значения этих
параметров.
на
основе экспериментальных данных, т.е.
задача - найти подходящие значения этих
параметров.
Множество результатов измерений
![]() величины
называется
выборкой объема
величины
называется
выборкой объема
![]() .
Для того, чтобы иметь возможность
воспользоваться аппаратом теории
вероятностей, целесообразно наблюдаемую
величину
рассматривать
как случайную величину, функцию
распределения которой
.
Для того, чтобы иметь возможность
воспользоваться аппаратом теории
вероятностей, целесообразно наблюдаемую
величину
рассматривать
как случайную величину, функцию
распределения которой
![]()
следует определить.
Полученный статистический материал
![]() ,
,
![]() ,
...
,
...![]() наблюдений представляет собой первичные
данные о величине, подлежащей статистической
обработке. Обычно такие статистические
данные оформляются в виде таблицы,
графика, гистограммы и т.д.
наблюдений представляет собой первичные
данные о величине, подлежащей статистической
обработке. Обычно такие статистические
данные оформляются в виде таблицы,
графика, гистограммы и т.д.
Если выборка объема
содержит
![]() различных
элементов
различных
элементов
![]() ,
причем
,
причем
![]() встречается
встречается
![]() раз,
то число
называется
частотой элемента
,
а отношение
раз,
то число
называется
частотой элемента
,
а отношение
![]() называется
относительной частотой элемента
.
Очевидно, что
называется
относительной частотой элемента
.
Очевидно, что
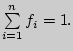
Вариационным (статистическим) рядом
называется таблица, первая строка
которой содержит в порядке возрастания
элементы
![]() ',
а вторая - их частоты
(относительные
частоты
',
а вторая - их частоты
(относительные
частоты
![]() .
.
Полигоном частот (относительных
частот) выборки называется ломаная с
вершинами в точках (
,
![]() )(
(
,
)).
)(
(
,
)).
Функция
![]() ,
где
-
объем выборки, а
,
где
-
объем выборки, а
![]() -
число значений
в
выборке, меньших
-
число значений
в
выборке, меньших
![]() ,
называется эмпирической функцией
распределения. Функция
,
называется эмпирической функцией
распределения. Функция
![]() служит
оценкой неизвестной функции распределения
служит
оценкой неизвестной функции распределения
![]() ,
т.е.
,
т.е.
![]() при n → ∞.
при n → ∞.
Пусть теперь
-
непрерывная случайная величина с
неизвестной плотностью вероятности
![]() .
Для оценки
по
выборке
.
Для оценки
по
выборке
![]() разобьем
область значений
на
интервалы длины
разобьем
область значений
на
интервалы длины
![]() .
Обозначим через
.
Обозначим через
![]() середины
интервалов, а через
число
элементов выборки, попавших в указанный
интервал. Тогда
середины
интервалов, а через
число
элементов выборки, попавших в указанный
интервал. Тогда
![]() -
оценка плотности вероятности в точке
.
В прямоугольной системе координат
построим прямоугольники с основаниями
-
оценка плотности вероятности в точке
.
В прямоугольной системе координат
построим прямоугольники с основаниями
![]() и
высотами
и
высотами
![]() ,
т.е. площади прямоугольника, равной
относительной частоте данного разряда.
Полученная таким образом фигура
называется гистограммой выборки.
,
т.е. площади прямоугольника, равной
относительной частоте данного разряда.
Полученная таким образом фигура
называется гистограммой выборки.
