
- •1,2. Уравнения Максвелла для монохроматических колебаний. Комплексные амплитуды полей
- •5. Тем волна (параметры)
- •7. Дивергенция вектора. Пребразования Остроградского-Гауса
- •8. Дивергенция вектора в прямоугольной системе координат.
- •12. Закон неразрывности магнитных силовых линий
- •13. Закон полного тока (Закон Ампера)
- •13. Продолжение
- •14. Закон электромагнитной индукции (Закон Фарадея)
- •15.Уравнение Маусвелла в дифференциальной форме
- •21. Проводимость сред. Закон Ома в диф. Форме.
- •21. Продолжение
- •22. Закон непрерывности зарядов.
- •23. Уравнение Максвелла для гармонических колебаний. Комплексная диэлектрическая проницаемость
- •24.Уравнение Гельмгольмца для плоской эм волны в однородном диэлектрике
- •26. Уравнение плоской волны. Связь между е и н волнами
- •26. Продолжение
- •27. Плоские волны с диэлектрическими потерями
- •31 Граничные условия на поверхность идеально проводящей среды.
- •34. Нормальное падение плоской электромагнитной волны на диэлектрическое полупространство
- •35. Плоские волны, распространяющиеся в произвольном направлении
- •36. Плоские электромагнитные волны с вращающейся поляризацией
- •38 Угол Брюстера
- •39 Полное внутреннее отражение Обратимся вновь к формулировке закона Снелля:
39 Полное внутреннее отражение Обратимся вновь к формулировке закона Снелля:
![]()
Здесь могут представиться два случая.
Оптическая плотность среды 2 превосходит оптическую плотность среды /, т. е. n2>«i- При этом условии всегда
 а
поскольку угол падения ср лежит в
интервале
а
поскольку угол падения ср лежит в
интервале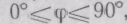 ,
преломленная волна существует при
любом угле падения.
,
преломленная волна существует при
любом угле падения.Среда 2 является оптически менее плотной, т. е. П2<п\. Здесь всегда t|)>q>, поэтому найдется такое значение угла падения, при котором преломленная волна пойдет параллельно границе раздела под углом i|i = 90°. Данное критическое значение угла падения носит название угла полного внутреннего отражения:
![]() (4.39)
(4.39)
При
углах падения
![]() преломленной
волны
преломленной
волны
в обычном представлении не существует, энергия падающей волны полностью отражается внутрь первой среды. Явление полного внутреннего отражения широко используется в оптике при создании призм, изменяющих направление пучка лучей (рис. 4.9). Подобные же устройства последнее время начали находить применение и в диапазоне СВЧ, например, на миллиметровых волнах.
Приведенный анализ эффекта полного внутреннего отражения является неполным, поскольку, с одной стороны, нет ответа на
вопрос о том, что происходит при углах падения <р,/больших, чем фпво. С другой стороны, было бы весьма целесообразно изучить структуру поля в среде 2 при наличии полного внутреннего отражения.
Обращаясь /к формуле (4.18) и предполагая п2<пг, видим, что при ф>фппо величина sin -ф должна быть больше единицы. Очевидно, что при любых вещественных значениях угла преломления такая ситуация невозможна. Тем не менее, известно, что синус, рассматриваемый как функция комплексного аргумента, может принимать любые, в том числе и сколь угодно большие значения. В соответствии с этим предположим, что при ф>срПво
угол преломления ф получает мнимое приращение. При этом можно записать
![]() (4.40)
(4.40)
Здесь а — мнимая часть угла преломления. Подставляя выражения (4.40) в .(4.13), получаем
![]() (4.41)
(4.41)
По математической форме данное соотношение весьма напоминает выражение для комплексной амплитуды плоской волны, распространяющейся в среде с потерями (см. § 2Л). Однако между ними существует принципиальная разница, так как в выражении (4.41) экспоненциальное уменьшение амплитуды волны происходит вдоль координаты г, в то время как волна распространяется вдоль координаты у. Такие волны носят название неоднородных плоских воли. С физической точки зрения неоднородная плоская вол-па распространяется вдоль границы раздела, как бы «прилипая» к ней. Указанная особенность дает основание назвать такие волны поверхностными волнами. В дальнейшем этот вопрос будет изучен более подробно.
На первый взгляд может показаться, что понятие комплексного угла преломления введено несколько искусственно. Однако, по-су-ществу, подобное расширение понятия плоской волны справедливо, поскольку комплексная амплитуда вида (4.41) служит решением уравнения Гельмгольца
![]()
в чем можно убедиться непосредственной подстановкой, приняв во
внимание,
что![]()
1.Векторы ЭМ поля в уравнениях Масквелла
2.Метод комплексных амплитуд
3.Уравнение волны в тригонометрической форме (смысл параметров)
4.Переход от тригонометрической формы к комплексной(уравнение плоской волны)
5.ТЕМ волны(параметры)
6.Основное свойство отрезка линии передачи ЭМ волны
7.Дивергенция вектора(определение).Преобразование Остроградского-Гаусса
8. Дивергенция вектора в прямоугольной системе координат
9.Ротор вектора(определение).Теорема Стокса
10.Ротор вектора в прямоугольной системе координат
11.Закон Гаусса в дифференциальной и интегральной формах(переход)
12.Закон непрерывности магнитных силовых линий(переход от диф. к интег.)
13.Закон Ампера(переход)
14.Закон Фарадея(переход)
15.Уравнение Максвелла в диф. форме(их физический смысл)
16.Уравнение Максвелла в интегральной форме.Их физический смысл
17.Электрическая и магнитная поляризации.Векторы поляризации.
18.Поляризация и намагничивание диэлектрика
19.Учёт поляризационных токов и зарядов в уравнениях Максвелла
20.Закон Кулона как следствие закона Гаусса
21.Проводимость сред.Закон Ома в диференциальной форме
22.Закон непрерывности зарядов
23.Уравнение Максвелла для гармонических колебаний.Комплексная диэелектрическая проницаемость
24.Уравнение Гельмгольца для плоской ЭМ волны в однородном диэлектрике
25.Свойства плоских волн и их параметров(волн сопротивление,фазовая скорость,длина волны поляризация)
26.Уравнение плоской волны.Связь между E и H волнами
27.Плоские волны в диэлектрике с потерями
28.Плоские волны в плохом проводнике(с потерями)
29.Граничные условия для нормальных составляющих векторов электрического и магнитного поля на границе раздела 2-х фаз
30. Граничные условия для тангенциальных составляющих
31.Граничные условия на поверхности идеально проводящей среды
32.Энергия ЭМ поля .Теория Умова-Пойтинга
33.Нормальное падение волны на идеально проводящую поверхность
34.Нормальное падение волны на диэлектрик
35.Распространение плоской волны в произвольном направлении
36.Плоская волна с круговой поляризацией
37.Падение плоской волны на границу раздела 2-х диэлектриков под произвольным углом: закон Снеля, перпендикулярная и параллельная поляризации
38.Случай полного прохождения. Угол Брюстера
39.Угол полного внутреннего отражения
