3 Методика вивчення теорем
Процес доведення теорем і геометрії виражає зв'язок одиничних суджень (креслення) і загальних (використання загальних властивостей фігур) тому при навчанні доказам для формування правильного уявлення про проблематичному характер того чи іншого судження слід застосовувати на кожному кроці питання "Чому?", "На якій підставі ? " У курсі планіметрії навчання доказам проводиться конкретно-індуктивним методом. Так як учні в курсі геометрії, на думку Шохор-Троцького, займаються переважно вирішенням завдань. Теореми вони доводять тільки такі, які не належать до числа очевидних для них і які не вимагають занадто тонких міркувань. Тому доцільно в деяких випадках пропонувати учням для виконання завдання абстрактного характеру, що готують самостійне формування або доказ теорем. Наприклад: встановити залежність між сторонами у трикутнику; або властивості бісектриси кута при вершині рівнобедреного трикутника емпірично. У процесі навчання у школярів повинно бути сформовано таке розуміння терміну "доказ": 1) допускаються істинними деякі відносини і факти (які складають умова теорем); 2) від умови до висновку будується логічна послідовна ланцюжок пропозицій, кожне з них має бути обгрунтовано за допомогою суджень, виражених в умові, визначень відомих понять, аксіом або раніше доведених тверджень; 3) висновок є останньою ланкою в ланцюжку цих логічно розташованих пропозицій. Наприклад: у курсі математики 5-6 класів цьому сприяють завдання з таким змістом: "Доповнити наведене доказ математичних тверджень, виконуючи зазначені вище вимоги, пропоновані до математичних доказів". "Якщо a: b = c, то a = bc. Довести " Умова: a: b = c. Висновок: a = bc.
Пропозиція |
обгрунтування |
1) a: b = c 2) a = bc |
1) умова 2) чому? |
У шкільному навчанні деякі
фрагменти математичної теорії
викладаються змістовно (неформально),
тому доказ також змістовні, тобто в них
використовуються звичайні міркування,
а правила логічного висновку не
фіксуються. Серед таких правил можна
виділити:
1) правило ув'язнення:
P; "якщо P, то Q" - висновок: "Q".
2)
правило введення кон'юнкції: P, Q - висновок
"P і Q".
3) правило силогізму:
"якщо P, то Q"; "якщо Q, то R" -
висновок "якщо P, то R".
4)
правило заперечення: "якщо A, то B",
"не B" - висновок "не А".
5)
правило контрапозиции: "якщо A, то B"
- висновок "якщо не B, то не A".
6)
правило розширеної контрапозиции: "якщо
A і B, то C" - висновок "якщо A і не С,
то не B".
7) Зведення до абсурду
- "якщо Г, А => B", "Г, А => не B"
- висновок "Г => не А", де Г - список
посилок.
Правило контрапозиции
і зведення до абсурду широко застосовується
у непрямих доказах, прикладом якого
може служити доказ від протилежного.
Непрямий
доказ деякої теореми Т полягає в
тому, що виходить із заперечення Т,
званого допущенням непрямого докази і
виводять з нього неправдивий висновок
застосуванням правила зведення до
абсурду.
Наприклад: якщо
а | | с, і b | | с, то a | | b. Припущення: a | | c і
b | | c, але a НЕ | | b. Згідно з визначенням
паралельних прямих отримуємо: якщо a НЕ
| | b => $ с (сÎа Ù сÎb), тому за правилом
введення кон'юнкції: з а | | c і b | | c. $ С
(сÎа Ù сÎb) маємо: a | | c і b | | c і $ с (сÎа Ù
сÎb). Але по аксіомі паралельних прямих
(з Т) невірно, що: a | | c і b | | c і $ с (сÎа Ù
сÎb), тобто з наших припущень вивели
протиріччя, яке й доводить
теорему.
Спеціальні форми
непрямого докази:
1) доказ методом
виключення: треба довести пропозиція:
"якщо B, то Q 1", інакше:
Г, Р => Q 1: поряд з
Q 1 розглядаються всі інші
можливості, які є: аксіомою, визначенням,
раніше доведеною теоремою чи наслідком
з них. Потім доводиться, що кожна з решти
можливостей, крім Q 1, веде
до протиріччя.
Наприклад: якщо
кожна площину, що перетинає пряму а,
перетинає і пряму b, то ці прямі
паралельні.
Потрібно встановити
проходження: "Г, Р" ® Q не | |; "Г"
і "a (якщо a'a, a'b) Þ a | | b.
Виходимо
з пропозицій: Q 1: a | | b, Q 2: a'b;
Q 3: ab - схрещуються.
Допущення
Q 2: a'b дає $ a (a'a і 
)
(Достатньо провести довільну площину
α через b, відмінну від площини визначається
пересічними прямими a і b) або: так як $ a
(a'a і 
)
<=> Не для всякої площині a (якщо a'a, то
a'b), отримуємо "якщо Q 2, то 
":
Якщо a'b, то не для всякої a якщо a'a, то
a'b).
З "якщо Q 2, то
"І"
Р "за правилом заперечення
маємо: 
:
.
Аналогічно допущення
Q 3: "ab схрещуються"
призводить до не будь-якій площині a
(якщо a'a, то a'b) (досить через b і яку-небудь
точку прямої a провести площину). Отримуємо
з: "якщо Q 3, то
"І"
Р "за правилом заперечення 
: 
.
Отже,
отримуємо 
і,
тобто Q 2 і Q 3 -
невірно, тому вірно Q 1: a | |
b.
2) Метод математичної
індукції - спеціальний метод докази,
застосовуваний до пропозицій типу: ""
xÎN P (x) ", тобто до пропозицій, що виражає
деякий властивість будь-натуральному
числу.
Схематично повна логічний
доказ теореми можна скласти так: 1) точне
поняття, 2) включаємо всі посилки; 3) не
опускають ніяких проміжних міркувань;
4) явно вказує правила виводу.
У
практиці шкільного навчання математики
найбільш часто використовується прямий
доказ, засноване на змістовному доказі
в згорнутому вигляді: 1) інтуїтивне
поняття, 2) опускають деякі зокрема,
загальні посилки; 3) опускають окремі
кроки; 4) не фіксують використання
логіки.
Наприклад: Діагоналі
прямокутника рівні.
Теорему можна
довести: а) за допомогою осьової симетрії,
б) за допомогою рівності прямокутників.
Зазначимо, що різні докази теореми
відрізняються як математичними посилками,
(які в них істинними пропозиціями даної
теорії), так і логікою (використовуваними
правилами).
Доказ 1.
"Якщо
чотирикутник - прямокутник, то його
діагоналі рівні" або "Якщо ABCD -
прямокутник, то AC = BD".
Точка D
симетрична A; B - симетрична C щодо MN (це
безпосередньо випливає з раніше доведеної
теореми: "Серединний перпендикуляр і
сторона прямокутника є віссю симетрії).
Значить, відрізок AC і DB симетричні
відносно осі MN. Тому AC = BD.
Доказ
2.
,
Тому що вони прямокутні ( 
),
AB = CD як протилежні сторони прямокутника;
AD - загальна сторона. Отже, AB = CD.
Методика
введення теорем передбачає підготовку
учнів до сприйняття її докази.
1) Для
того, щоб учні зрозуміли логічні частини
докази, застосовують метод доцільних
завдань.
Наприклад: При
доведенні того факту, що кут між бічним
ребром призми і її висотою дорівнює
куту між площинами підстави і перпендикулярного перетину,
необхідного попередньо вирішити за
готовими кресленнями наступні завдання:
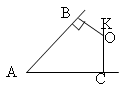
A |
B |
K |
O |
C |
|
|
|
|
|
|
|
|
|
1. За даними на малюнку знайти
і
кут між прямими BO і OC. Зауваження: кут між двома прямими (двома площинами) гострий.
|
|
B |
A |
O |
|
|
|
|
|
|
|
|
|
2. Кут між площинами
і 
дорівнює 
,
Пряма OA перпендикулярна площині
, 
;
Пряма OB перпендикулярна площині
, 
.
Знайти кут між прямими OA і OB. 2) Для підготовки учнів до сприйняття докази теореми можна використовувати прийом багаторазового докази (наприклад, потрійна прокручування).
а) учитель викладає схему (ідею, канву) докази. Можливо, при цьому використання евристичної бесіди, яка може бути або анаREF SHAPE \ * MERGEFORMAT литик-синтетичний або синтетичний. Питання повинні бути сформульовані чітко, відображаючи найбільш важливі логічні етапи докази. Після кожного питання необхідна пауза для того, щоб учні змогли самостійно знайти відповідь:
б) вчитель викладає доказ теореми у вигляді короткого оповідання, обгрунтовуючи кожен крок;
в) повторення докази у повному обсязі.
Ще один прийом навчання доказом - навчання учнів складеного плану докази теореми, при якому виконуються наступні етапи:
· Дається готовий план докази нової теореми і учням пропонується самим довести її за допомогою плану. Переваги: 1) план розбиває доказ теореми на ряд простих, елементарних завдань, які учні можуть вирішити, 2) у учнів з'являється впевненість у тому, що вони зможуть довести нову теорему, 3) план дозволяє охопити всі доказ у цілому, в учнів виникає відчуття повного розуміння;
· Учнів вчать складати план вже вивченої теореми. Спочатку ця робота виконується колективно, а потім самостійно.