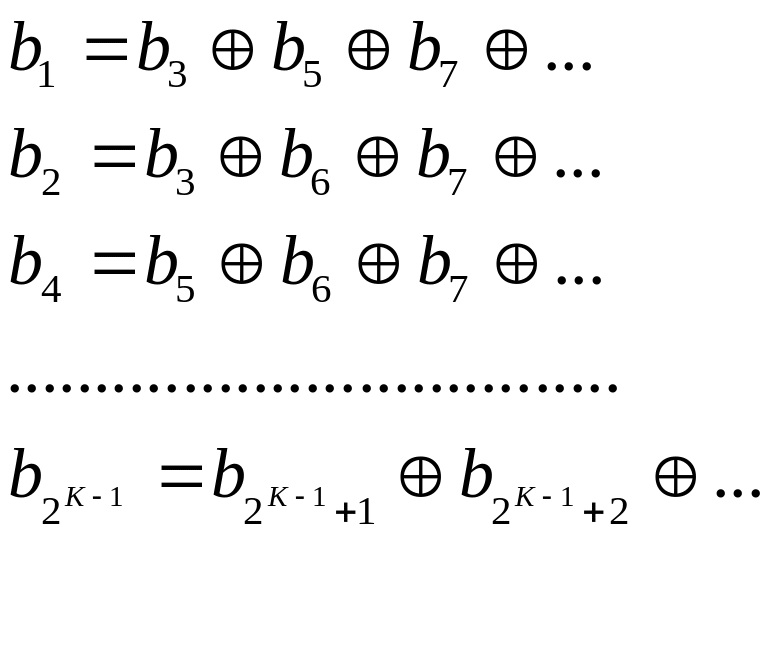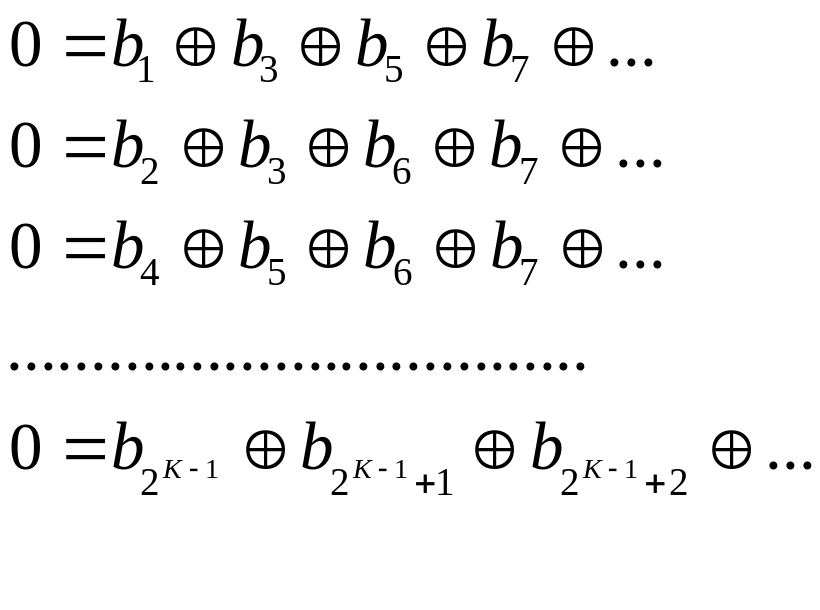Для кода имеем разбиение . Отсюда исходное сообщение есть .

Коды Хэмминга относятся к методам равномерного кодирования.

Рассматривается случай, когда исходный и кодирующий алфавиты являются двоичными, т.е. . В этом случае 1 символ слова соответствует 1 двоичному разряду.

Пусть – код сообщения . При передаче кода по каналу связи на выходе канала связи получают слово .

Способ кодирования, называемый кодом Хэмминга, позволяет по коду сообщения на выходе канала связи не только обнаружить, но и однозначно восстановить код , а значит и исходное сообщение , если известно, что при передаче кода возможно искажение не более 1 разряда.

Построение кода Хэмминга.

Построение кода Хэмминга происходит в несколько этапов.

I. Нахождение числа k контрольных разрядов.

При передаче кода , очевидно, возможны следующие варианты получения кодов на выходе канала связи (рис.2.15).

П ервый вариант сообщения на выходе канала связи не содержит искажений, остальные – по одному искажению разряда. Таким образом, число вариантов равно .

Количество k контрольных разрядов в коде сообщения определяется таким образом, чтобы по их содержимому можно было однозначным образом определить, какой разряд сообщения искажен, т.е. в каком из вариантов передано сообщение.

Содержимое контрольных разрядов – двоичное слово длины k. Для однозначного соответствия этим словам различных вариантов передачи сообщения, очевидно, должно выполняться условие:

(2.6)

Отсюда определяется k как наименьшее целое, удовлетворяющее этому условию . Преобразуем неравенство (2.6). Учитывая, что и подставляя разность в (2.6), получаем

(2.7)

Отсюда при известном значении m можно выбрать как наименьшее целое, удовлетворяющее (2.7), а затем вычислить . Ясно, что при этом должна быть уверенность, что передача кода длины l не вызовет искажения более одного разряда.

II. Выделение из отрезка натуральных чисел k последовательностей.

Пусть V–натуральное число из отрезка и – его двоичная запись, т.е. . Поскольку число изображается в двоичной системе счисления записью 10…0, содержащей 1 только в - м разряде, то отсюда и из условия (1.6) следует, что любое число из отрезка в двоичном представлении имеет не более k разрядов.

1) В первую последовательность включим все натуральные числа V из отрезка , в двоичном представлении которых первый разряд равен 1, т.е. . Этими числами являются

1 ,	2 ,	5 ,	7 ,	9 ,….
1	11	101	111	1001

Нижняя строка содержит двоичные числа указанных чисел.

2) Во вторую последовательность включаются все числа V , второй разряд, равный 1, т.е. :

2 ,	3 ,	6 ,	7 ,	10 ,….
10	11	110	111	1010

3) В третью последовательность включаются числа с :

4 ,	5 ,	6 ,	7 ,	12 ,….
100	101	110	111	1100

………………………………………………………………..

k) B k-последовательности все числа имеют

2 k-1 ,	2 k-1 +1 ,…
10…00	10…01

Первыми членами этих последовательностей являются степени двойки: . Те разряды набора , у которых индекс I является степенью двойки, являются контрольными, остальные – информационными. Контрольных разрядов будет ровно k, информационных .

III. Определение содержимого информационных разрядов.

В информационные разряды (разряды с номерами, не являющимися степенью двойки) записываются последовательно двоичные символы сообщения :

и т. д.

IV. Определение содержимого контрольных разрядов.

Содержимое контрольных разрядов определяется по формулам:

(2.8)

Таким образом, есть сумма по модулю 2 содержимого всех разрядов с номерами, принадлежащим первой последовательности, кроме ее первого члена, есть аналогичная сумма по второй последовательности и т. д.

Все разряды, указанные в правой части равенств являются информационными. Их содержимое определено ранее.

По сути, каждое равенства (2.6) задают код с проверкой на четность для каждой выделенной последовательности кроме ее первого элемента, а значение контрольной суммы записывается не в последний, а в первый разряд каждой последовательности.

В этом случае проверочными соотношениями являются:

(2.9)

Первое равенство в (2.9) получается из первого равенства (2.8), если прибавить по модулю 2 слева и справа элемент , второе — получается из второго равенства в (2.8), если прибавить слева и справа и т. д.

Пример 1. Пусть известно, что l=7.

I. Из (2.6) получим, что k=3, а m=l-k=4. Определим, какой код будет

иметь, например, сообщение .

II. Получим три последовательности:

1, 3, 5, 7 — первая последовательность,

2, 3, 6, 7 — вторая последовательность,

4, 5, 6, 7 — третья последовательность.

III. Заполняем информационные разряды коды (рис.2.16)

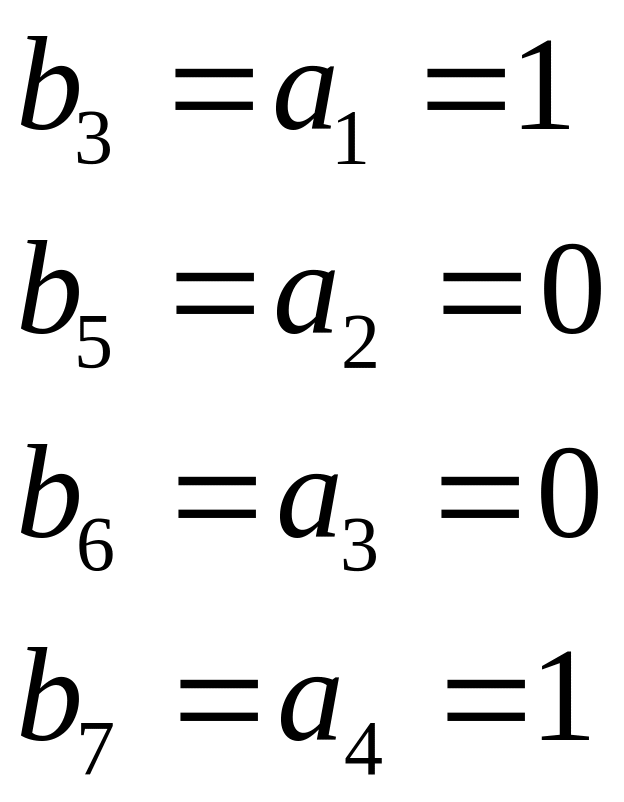
		1		0	0	1
Рис.2.16

IV. Определяем содержимое контрольных разрядов согласно (2.8):

– суммирование по первой найденной

последовательности,

– суммирование по второй найденной

последовательности

– суммирование по третьей найденной

последовательности

Заполняя контрольные разряды, получаем код (рис. 2.17).

0	0	1	1	0	0	1
Рис.2.17

Пример 2. Определим код Хэмминга для слова .

1. С помощью (2.7) подбираем l=9, тогда k=9-5=4. Контрольными разрядами являются 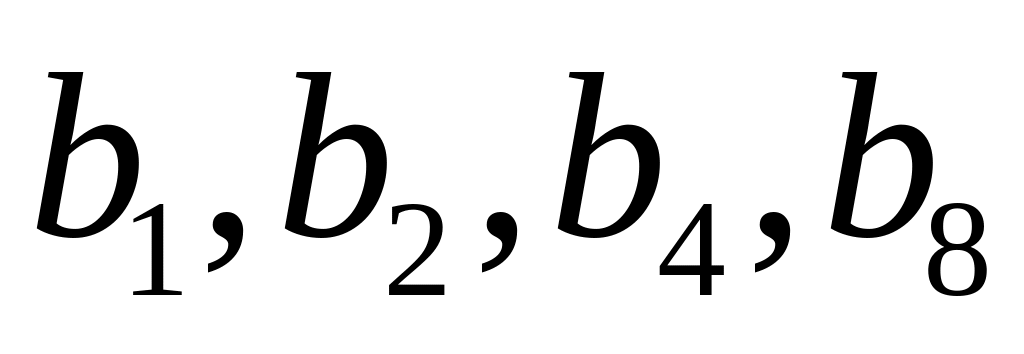в коде, остальные – информационные.

II. Выделенные последовательности имеют вид:

1, 3, 5, 7, 9 – первая последовательность,

2, 3, 6, 7 – вторая последовательность,

4, 5, 6, 7 – третья последовательность,

8,9 – четвертая последовательность.

III. После заполнения информационных разрядов имеем (рис.2.18):

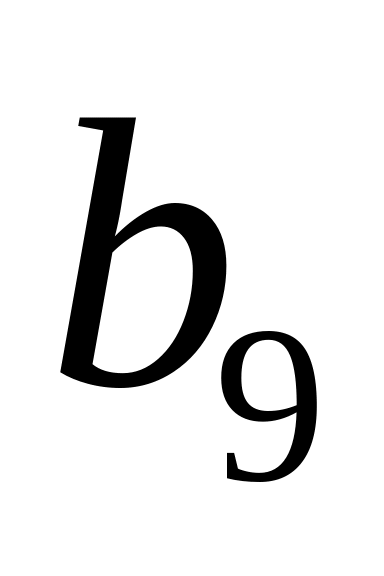
		0		1	1	1		0
Рис.2.18

IV. Подсчитываем содержимое контрольных разрядов:

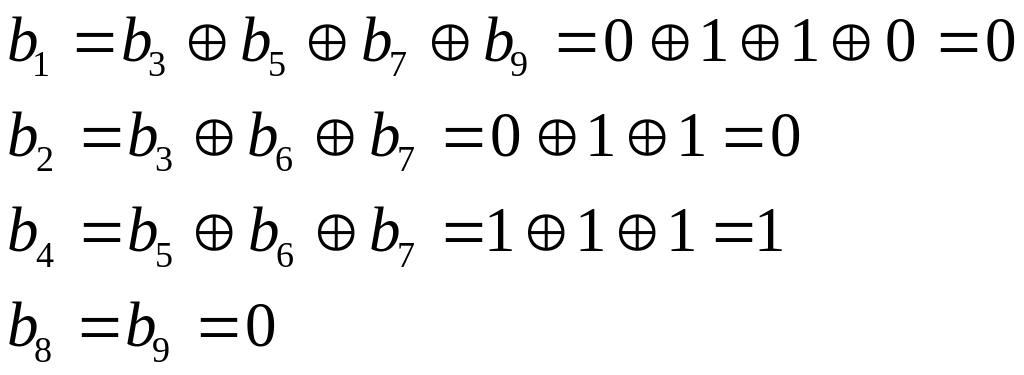
После заполнения контрольных разрядов имеем код .