Тема: Теория потребительского выбора

15. Определите, какое количество товаров х и у будет приобретать потребитель, чтобы максимизировать полезность, если его доход составляет 100 ден. ед., цены товаров х и у соответственно равны Рх = 10 ден. ед., Ру = 5 ден. ед. Функция полезности имеет вид: U(х, у) = ху.

16. Дано: Рх = 8 ден. ед., Ру = 4 ден. ед., I (доход) = 64 ден. ед. Определите, какая из следующих пар точек, характеризующих потребительский выбор индивида, не лежит на бюджетной линии?

а) х = 0; у = 16;

б) х = 3; у = 10;

в) х = 3; у = 8;

г) х = 8; у = 0.

17. Цены товаров х и у равны соответственно 10 и 5 ден. ед., доход потребителя равен 100 ден. ед. Определите точки пересечения бюджетной линии с осью абсцисс и осью ординат. Рассчитайте наклон бюджетной линии.

18. Индивид покупает 8 единиц товара х и 4 единицы товара у. Определите его доход, если известно, что цена товара х равна 2 ден. ед., а предельная норма замены равна 0,5.

19. Определите цены товаров х и у, если известно, что доход индивида равен 100 ден. ед., объем потребления товаров х и у равен соответственно 10 и 30, а цена товара х в два раза больше цены товара у.

20. Дана функция спроса индивида на товар х: Q_dх = 10 – Р. В точке А эластичность функции спроса на товар Х является единичной. В исходной ситуации индивид приобретает товар Х по цене 3 ден. ед. Определите, как изменится спрос на товар у при росте цены на товар Х до 7 ден. ед.

21. Потребитель имеет доход 100 ден. ед. Цена товара у равна 20 ден. ед., цена товара х -- 10 ден. ед. Функция полезности U(х, у) = ху. Определите эффекты дохода и замены, если цена товара х увеличилась до 20 ден. ед.

22. Функция полезности потребителя U(х, у) = ху; цена товара х – Рх = 4 ден. ед.; цена товара у – Ру = 1 ден. ед.; доход потребителя I = 80 ден. ед. Цена товара х увеличивается в два раза. Определите: а) потребление товаров х и у до изменения цены товара х; б) после изменения цены товара х; в) эффект замены и эффект дохода.

23. Даны функции спроса и предложения:

Qd(Р) = 10 – Р; Qs(Р) = 2р – 8

Определите:

а) величину выигрышей потребителей (W_d ) и производителей (W_s);

б) как изменятся выигрыши потребителей и производителей при введении потоварного налога на производителей в 3 ден.ед.;

Найдите общую сумму собранного налога.

24. Даны функции спроса и предложения:

Qd(Р) = 150 – 3Р; Qs (Р) = - 10 + 2Р

Определите:

а) равновесные цену и объем продаж;

б) правительство ввело фиксированную цену на товар на уровне 30 тыс.руб. за единицу. Рассчитайте объем дефицита на рынке.

25*. Индивид покупает 8 единиц товара Х и 4 единицы товара У. Определите его доход, если известно, что цена товара Х равна 2 ден.ед., а предельная норма замещения – равна 4.

Решение:

Доход индивида равен: I = Qх х Рх + Qу х Ру,

В этой формуле неизвестна цена товара У. Ее можно найти из предельной нормы замещения: MRS = Рх/Ру = 4, отсюда Ру = Рх/4 = 2/4 = 0,5 ден.ед.

I = 8 х 2 + 4 х 0,5 = 18 ден.ед.

Ответ: денежный доход индивида равен 18 ден.ед.

26*. Доход потребителя составляет 600 рублей.

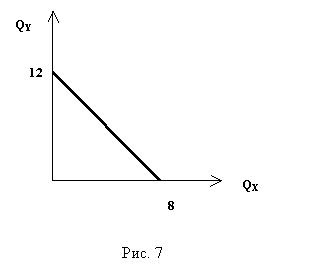
Используя данные рис. 7, определите:

а) Рх и Ру;

б) наклон бюджетной линии;

в) уравнение бюджетной линии.

Р ешение:

Если Q_х = 0, то Q_у = I/Ру , следовательно Р_у = I/Qу = 50 ден.ед.

Если Q_y = 0, то Q_x = I : P_x, следовательно P_x = I : Q_x = 75 ден. ед.

б) Наклон бюджетной линии определим из уравнения бюджетного ограничения:

I = P x Q_x + P_yQ_y.

Он равен соотношению: P_x : P_y и, соответственно, равен: 75 : 50 = 3/2 = 1,5;

в) уравнение бюджетной линии: I = P x Q_x + P_yQ_y, и соответственно: Q_y = -3/2Q_x + 12.