13.Ряды

13.1. Числовые ряды Основные понятия числового ряда

Определение . Пусть дана бесконечная числовая последовательность u₁, u₂,¼,u_n,¼. Выражение вида

u₁+u₂+u₃+¼+u_n+¼= (13.1.1)

называется числовым рядом,числа u₁, u₂,¼,u_n,…- членами ряда, член u_n -общим членом ряда ( это формула, . по которой для любого номера n можно определить соответствующий член ряда).

Определение. Сумма конечного числа п первых членов ряда называется его n-й частичной суммой:

S_n=u₁+u₂+u₃+¼+u_n.

Рассмотрим частичные суммы ряда (1)

S₁= u₁, S₂= u₁+u₂, S₃= u₁+u₂+u₃, ¼, S_n= , ¼

Определение. Если существует конечный предел при п®∞ последовательности частичных сумм членов данного ряда

,

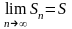то ряд (13.1.1) называется сходящимся, а число S-его суммой:

S = .

Если же данный предел не существует или бесконечен (т.е. S_n®∞ при п®∞ ), то ряд (13.1.1) расходится и суммы не имеет.

Геометрическая прогрессия

Определение 4. Геометрической прогрессией называется ряд

a+aq+aq²+¼+aqⁿ+¼=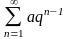 , (13.1.2)

где q-знаменатель ряда (действительное число)

Этот ряд сходится при |q|<1 и расходится при |q|³1.

Действительно, согласно известной формуле при q≠1

S_п=

а) если |q|<1, то 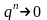при п®∞, тогда имеем

ряд сходится и его сумма .

б) в случае |q|>1: 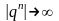при п®∞ и S_n=±∞.

в) при q=1 ряд (13.1.2) имеет вид: a+a+a+¼= , S_n=na, , т.е. ряд расходится.

г) q=-1 ряд (13.1.2) имеет вид: a-a+a-а+¼ В этом случае

предела не имеет и ряд расходится.

Свойства сходящихся рядов

Теорема 13.1. Если сходится ряд , полученный из данного ряда (13.1.1) путём отбрасывания его первых п членов, то сходится и сам данный ряд. Обратно, если сходится ряд (13.1.1), то сходится и ряд, полученный из данного ряда путём отбрасывания первых п членов. Т.е. на сходимость ряда не влияет отбрасывание конечного числа его первых членов.

Теорема 13.2. Если ряд (13.1.1) сходится и его сумма равна S, то и ряд

, (13.1.3)

где с-некоторое число, также сходится, и его сумма равна c×S.

Теорема 3. Если ряды и сходятся и их суммы равны соответственно S и , то и ряд

(13.1.4)

тоже сходится и его сумма равна S± .

Необходимый признак сходимости

Теорема 13.4. Если ряд (13.1.1) сходится, то его общий член стремится к нулю при неограниченном возрастании п, т.е.

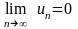. (13.1.5)

Доказательство. По условию ряд (13.1.1) сходится. Обозначим через S его сумму. Рассмотрим частичные суммы ряда

S_n=u₁+u₂+¼+u_n и S_n-1=u₁+u₂+¼+u_n-1.

Отсюда S_n- S_n-1= u_n. Так как S_n®S и S_n-1®S при n®∞, то

.Теорема доказана.

Следствие. Если предел общего члена ряда не равен нулю при n®∞, то данный ряд расходится.

Условие является необходимым, но не достаточным условием сходимости ряда. Далее будет доказано, что так называемый гармонический ряд 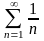является расходящимся, хотя .
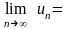
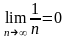