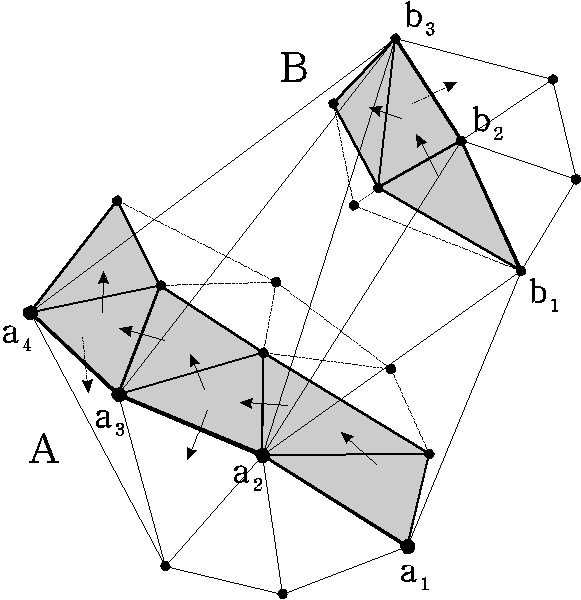
Метод “разделяй и властвуй”

Известная нижняя оценка для задачи построения выпуклой оболочки в трехмерном пространстве такая же, как и в двумерном: . Алгоритмdivide-and-conquer был предложен в [5], и достигает требуемой нижней оценки. Позже в [3] были внесены важные корректировки в алгоритм по сравнению с оригинальной статьей. Алгоритм является обобщением алгоритма построения выпуклой оболочки на плоскости с мостиками на основе линейной разделимости.

Принцип алгоритма такой же, как и в двумерном пространстве: отсортировать точки по координате, разделить их на два множества, рекурсивно построить выпуклую оболочку в каждом из множеств и слить в одно. Слияние может быть сделано за сложность, таким образом, общая сложность составляет.

О’Рурк [6] так комментировал этот алгоритм в своей книге: “этот алгоритм важен теоретически и сам по себе довольно красив. Однако его довольно трудно реализовать, и, кажется, он не применим на практике, в отличие от асимптотически более медленных алгоритмов…". Первое полное описание построения выпуклой оболочки в 3D методом “разделяй и властвуй” было представлено Эдельсбрунером в [7]. Позже Дэй описал реализацию этого алгоритма в [8], однако реализация была излишне сложной и асимптотически не оптимальной (со сложностью ).

Ниже приводится псевдокод алгоритма divide-and-conquer, с учетом того, что на вход подается отсортированное множество по координате .

Algorithm DIVIDE-AND-CONQUER(P)  CH(P)

1. if ()then

2. построить любым методом

3. return

4. 

5. 

6. 

7. 

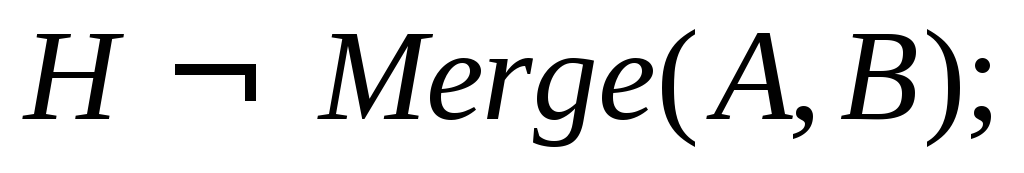
8. return

Предварительная сортировка элементов множества по координатетребуетопераций. Благодаря сортировке и тому, как выполняется шаги 4-5 алгоритма, множества и представляют два непересекающихся трехмерных политопа. Основная сложность заключается в выполнении функции за время : необходимо построить цилиндрическую триангуляцию, опирающуюся на выпуклые оболочки и по некоторым контурам и удалить из и части, оказавшиеся скрытыми. В выпуклой оболочке добавится некоторый ”обод” из граней с топологией цилиндра без оснований (cм. рисунок 6). Количество граней линейно от размера двух политопов: каждая грань использует как минимум одно ребро из или , таким образом количество граней не более чем общее количество ребер.

Рассмотрим шаг слияния двух оболочек более подробно: сначала будет описана процедура слияния двух выпуклых оболочек из [1], а затем будут предложены улучшения.

Рисунок 6 Политопы до соединения. Результирующая выпуклая оболочка. Жирные ребра показывают границу новых граней.

Рассмотрим слияние выпуклых оболочек.

В [3] для представления структуры выпуклой оболочки используется реберный список с двойными связями (РСДС). Укрупнено шаг слияния можно представить следующим образом:

1. Построить цилиндрическую триангуляцию .

2. Удалить из A и B части оказавшиеся скрытыми в результате построения триангуляции .

Основываясь на интуитивном уровне, построение триангуляции можно рассматривать как операцию заворачивания подарка. Хотя может иметьграней, а каждый шаг заворачивания в общем случае требуетопераций, использование особенностей трехмерных политопов позволяет решить эту задачу за линейное время.

Построение триангуляции начинается с нахождения некоторого ее ребра. Наиболее удобный способ состоит в проектировании выпуклых оболочек A и B на плоскость XOY и затем нахождении нижнего мостика e [3] (таким образом можно поддерживать нижнюю выпуклую оболочку проекции точек на XOY) (см. рисунок 7). Имея ребро e можно начать построение , выбрав в качестве опорной плоскость, проходящую через реброe параллельно оси OZ.

На очередном шаге построения в качестве базы используется последняя построенная грань триангуляции. Пусть граньявляется базовой на текущем шаге. Теперь среди вершин, смежных снеобходимо выбрать вершинутак, чтобы граньобразовала наибольший выпуклый угол ссреди всех граней.

Рисунок 7 Начальный и последующие шаги построения процедуры построения

Аналогичным образом, среди всех вершин, смежных с , выберем вершину. Теперь, когда выявлены два претендентаи, делается заключительное сравнение: еслиобразует сбольший выпуклый угол, чем, тодобавляется к(в противном случае добавляется), и на этом шаг заканчивается. Используя тот факт, что в РСДС можно эффективно проходить ребра, инцидентные некоторой вершине в порядке обхода по часовой стрелке или против нее, можно хранить информацию о пройденных вершинах для выпуклых оболочек следующим образом (см. рисунок 8).

Рисунок 8 Шаг, обеспечивающий продвижение при построении (s=4).

Пусть грань образует наибольший выпуклый угол сиз всехсi=2,…,k. Любое ребро , при 1<i<s оказывается внутри выпуклой оболочки , и поэтому его можно исключить из дальнейшего рассмотрения. Просмотр ребер, инцидентных, следует начинать с последнего из просмотренных ребер, так как все другие удалены. Таким образом, на заворачивание требуетсяопераций.

Удаление из ичастей оказавшихся скрытыми можно сделать за линейное время от размера удаляемых частей (процесс удаления можно охарактеризовать как обход структуры, начиная с заведомо удаляемой грани, и не переходящий через ребра, помеченные как принадлежащие “ободам” цилиндрической триангуляции).

Таким образом, слияние иможет быть выполнено за время.

Построение цилиндрической триангуляции можно упростить, если хранить неполную информацию о РСДС: можно исключить хранение информации о ребрах выпуклой оболочки. Для построения цилиндрической триангуляции достаточно информации о структуре политопов из ссылок между гранями (каждая грань имеет три ссылки на соседние граци в порядке обхода по часовой стрелке).

Таким образом, вместо того, чтобы обходить ребра, инцидентные вершине в порядке обхода против часовой стрелке, достаточно обойти грани сливаемых выпуклых оболочек, имеющие общие ребра с ободом цилиндрической триангуляции, и которые будут скрыты после слияния (т.е. внутренние грани). Обход граней производится по ободу цилиндрической триангуляции (см. рисунок 9).

Рисунок 9 Построение цилиндрической триангуляции при обходе граней, смежных с ободом цилиндрической триангуляции.

Пройденных граней будет не более чем общее количество граней в сливаемых оболочках, и, следовательно, общая сложность слияния есть .

Заметим, что не может быть однозначно идентифицирована в случае, когда грани цилиндрической триангуляции копланарны с гранями сливаемых выпуклых оболочек (например, при распределении точек на кубе этот случай встречается довольно часто). В таком случаем можно встретить проблемы с построением, что и было сделано в [8] (именно вследствие этого сложность реализации получилась, а цилиндрическая триангуляция не всегда односвязной). На рисунке 10 проиллюстрирована эта ситуация.

Рисунок 10 Неоднозначность построения цилиндрической триангуляции . Грани, помеченные одним цветом, лежат в одной плоскости. Триангуляцияможет опираться как на внешний или внутренний обод, так и на любой из промежуточных ободов.

Дэй в [8] приводит реализацию для внешнего обода, однако лучше строить цилиндрическую триангуляцию для внутреннего обода и, таким образом, упростить обработку частных случаев. Для выявления кандидата на включение в триангуляцию на следующем шаге, в случае копланарности граней-кандидатов, нужно брать ту грань, которая полностью принадлежит другой грани, если ни одна не входит в другую, можно брать произвольную.

После построения цилиндрической триангуляции можно обновить структуру РСДС за линейное время. Заметим, что при таком подходе к построению цилиндрической триангуляции существенно упрощается удаление скрытых частей сливаемых оболочек. Как отмечает О’Рурк в [6], обод цилиндрической триангуляции необязательно должен образовывать простой цикл из ребер на (и аналогично) (см. рисунок 11).

Рисунок 11 клин и параллелепипед; выпуклая оболочка, полученная в результате слияния

Используемая память: на хранение сливаемых выпуклых оболочек и на хранение цилиндрической триангуляции требуется хранение примерно граней в худшем случае, что превосходит в два раза просто хранение граней выпуклой оболочки.