
- •Расчет и проектирование водонагревателей Учебно-методическое пособие по курсу «Тепломассообмен»
- •443001 Самара, ул. Молодогвардейская, 194
- •Содержание
- •Общая часть
- •1 Классификация теплообменных аппаратов
- •2 Основы теории расчёта рекуперативных теплообменных аппаратов на стационарных режимах
- •3 Расчёт теплообменных аппаратов с использованием метода безразмерных характеристик
- •3.1 Безразмерные характеристики
- •3.2 Использование метода безразмерных характеристик для расчета рекуперативных теплообменных аппаратов
- •3.3 Применение метода безразмерных характеристик для расчёта регенеративных теплообменников
- •4 Гидравлический расчет теплообменных аппаратов
- •5 Определение коэффициента удержания тепла в рекуперативных теплообменных аппаратах
- •5.1 Теплоотдача при свободной конвекции в неограниченном пространстве
- •5.2 Теплообмен излучением между твердыми телами
- •6 Особенности конструирования трубной решетки водонагревателя
- •7 Конструкции водонагревателей
- •7.1 Конструкция водоводяного подогревателя
- •7.2 Конструкция пароводяного подогревателя
- •Контрольные вопросы
- •8 Примеры расчета водонагревателей
- •Библиографический список
3 Расчёт теплообменных аппаратов с использованием метода безразмерных характеристик
Метод
безразмерных характеристик, предложенный
В.М. Кейсом
и А.Л. Лондоном [1],
основывается на использовании безразмерных
характеристик –
эффективности теплообменника (![]() )
и безразмерного числа единиц переноса
тепла (NTU).
По сравнению с традиционным методом
расчёта теплообменных аппаратов,
использующим величину среднелогарифмического
температурного напора Δtср,
метод безразмерных характеристик имеет
преимущества при выполнении поверочного
расчёта, так как позволяет по аналитическим
зависимостям определять сразу конечные
температуры теплоносителей, не прибегая
к большому числу приближений.
)
и безразмерного числа единиц переноса
тепла (NTU).
По сравнению с традиционным методом
расчёта теплообменных аппаратов,
использующим величину среднелогарифмического
температурного напора Δtср,
метод безразмерных характеристик имеет
преимущества при выполнении поверочного
расчёта, так как позволяет по аналитическим
зависимостям определять сразу конечные
температуры теплоносителей, не прибегая
к большому числу приближений.
Результаты расчёта большого числа теплообменных аппаратов с различными схемами движения теплоносителей представлены в монографии [1] как в виде аналитических зависимостей, так и в табличной и графической формах.
3.1 Безразмерные характеристики
Эффективность теплообменника, согласно [1], определяется выражением:
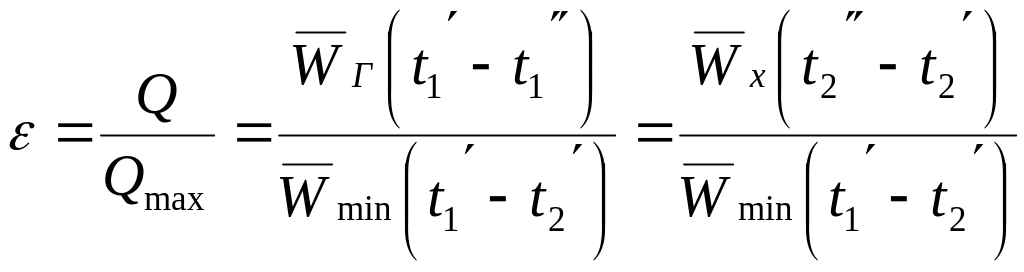 ,
(3.1)
,
(3.1)
где
![]() –
максимально возможное количество тепла,
которое может быть передано в идеальном
противоточном теплообменнике с бесконечно
большой теплопередающей поверхностью,
кВт;
–
максимально возможное количество тепла,
которое может быть передано в идеальном
противоточном теплообменнике с бесконечно
большой теплопередающей поверхностью,
кВт;
![]() –
водяные
эквиваленты горячего и холодного
теплоносителей соответственно, кДж/
ºС;
–
водяные
эквиваленты горячего и холодного
теплоносителей соответственно, кДж/
ºС;
![]() –
наименьшее
значение водяного эквивалента из величин
–
наименьшее
значение водяного эквивалента из величин
![]() .
.
Пренебрегая зависимостью теплоёмкостей теплоносителей от температуры, выражения для определения эффективности теплообменника принимают вид:
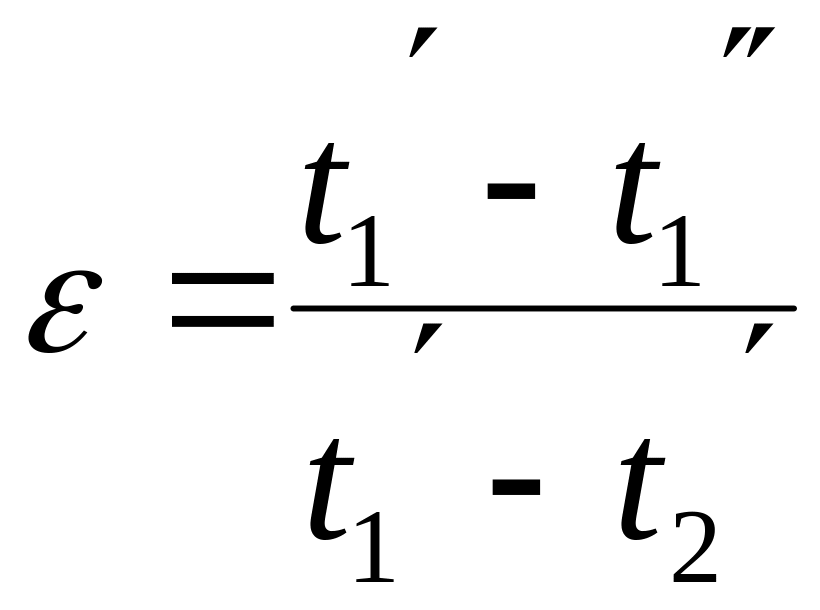 ,
при
,
при
![]() ;
(3.2)
;
(3.2)
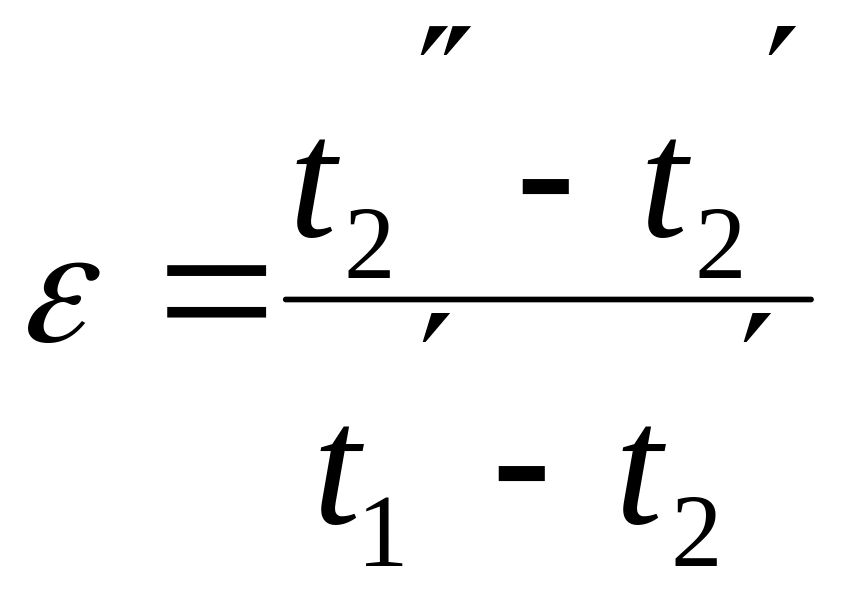 ,
при
,
при
![]() .
(3.3)
.
(3.3)
При
проведении поверочного расчёта значения
температур теплоносителей на выходе
из теплообменника
![]() и
и
![]() подлежат определению из уравнений
(3.2), (3.3).
подлежат определению из уравнений
(3.2), (3.3).
Следующей
безразмерной характеристикой, определяющей
возможности передачи тепла от одного
теплоносителя к другому, является
безразмерное число единиц переноса
тепла
![]() ,
определяемое по формуле:
,
определяемое по формуле:
![]() ,
(3.4)
,
(3.4)
где – коэффициент теплопередачи, Вт/м2·ºС;
– поверхность теплообмена, м2.
Число единиц переноса теплоты позволяет оценить возможности достижения больших значений эффективности с учётом капитальных затрат, массы и объёма для данной поверхности теплообмена, а также с точки зрения затрат энергии на преодоление гидравлического сопротивления при повышении коэффициента теплопередачи.
Для нахождения значения эффективности теплообменного аппарата используют аналитические зависимости вида:
![]() .
(3.5)
.
(3.5)
Получим
вид функциональной зависимости для
противоточного теплообменника.
Предположим, что
![]() ,
т.е.
,
т.е.
![]() .
.
Исходя из баланса энергии, получаем:
![]() ,
(3.6)
,
(3.6)
или
![]() .
(3.7)
.
(3.7)
Решая совместно уравнение (3.7) и уравнение теплопередачи
![]() ,
,
получаем:
![]() .
(3.8)
.
(3.8)
Интегрирование этого выражения в пределах поверхности нагрева теплообменника приводит к уравнению:
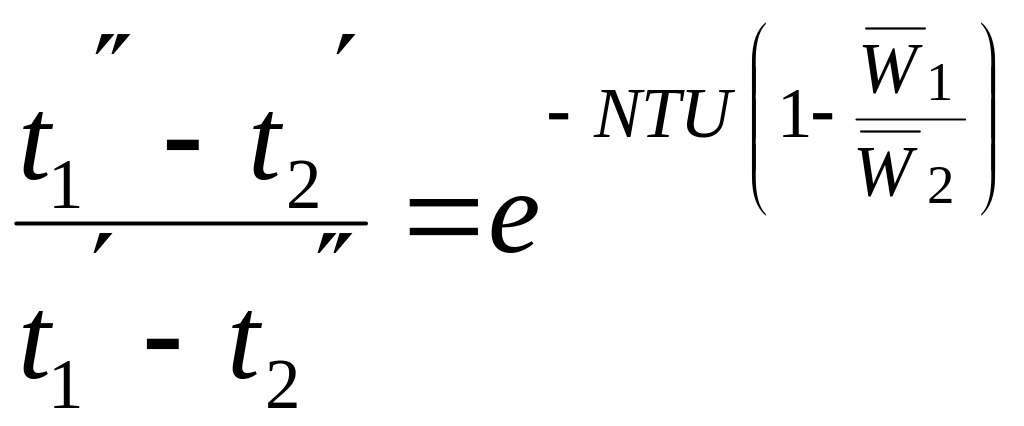 .
(3.9)
.
(3.9)
Температурные
условия в противоточном теплообменнике
с
![]() схематически представлены на рис. 3.1.
схематически представлены на рис. 3.1.
Рабочая
линия, выражающая зависимость
![]() от
от
![]() имеет наклон
имеет наклон
![]() .
(3.10)
.
(3.10)
Кроме
того,
![]() m
для принятого условия
m
для принятого условия
![]() .
Рабочая линия нанесена на рис. 3.2. Там
же нанесена линия, соответствующая
тепловому равновесию между двумя
потоками, когда
.
Рабочая линия нанесена на рис. 3.2. Там
же нанесена линия, соответствующая
тепловому равновесию между двумя
потоками, когда
![]() .
.
Из
графика следует, что разность между
двумя линиями, определённая в данной
точке с координатами
![]() ,
должна быть равна
,
должна быть равна
![]() ,
что вытекает из зависимости температурных
условий от величины поверхности
теплопередачи (рис. 3.1).
,
что вытекает из зависимости температурных
условий от величины поверхности
теплопередачи (рис. 3.1).
Из
определения эффективности
![]() следует следующее выражение:
следует следующее выражение:
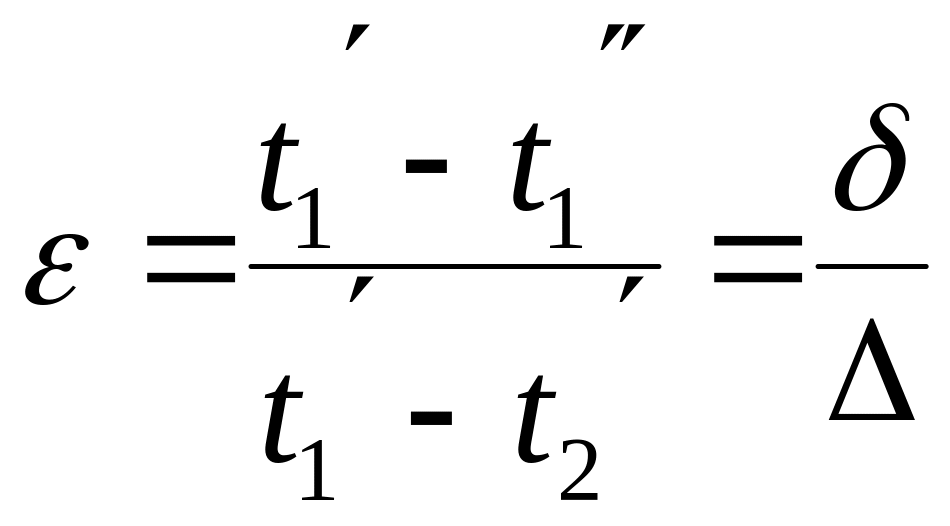 .
.
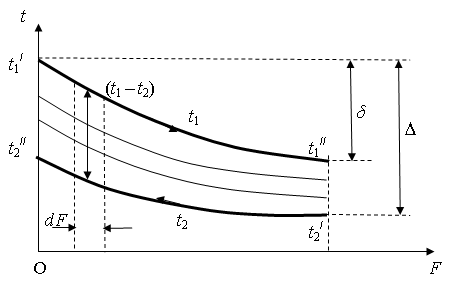
Рис.
3.1 Характер изменения температур для
противотока при
![]()
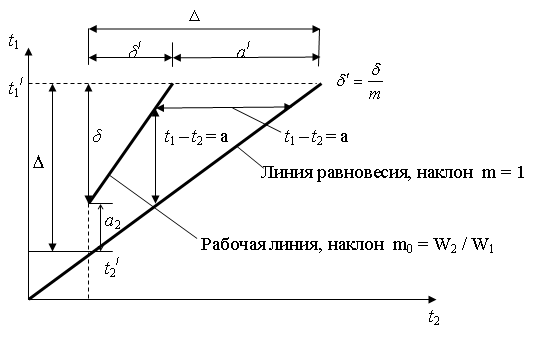
Рис.
3.2 График «рабочая линия – линия
равновесия»
для противотока при
![]() <
<![]()
При рассмотрении графика «рабочая линия – линия равновесия» можно обнаружить, что
![]() ;
;
![]() .
.
Таким образом,
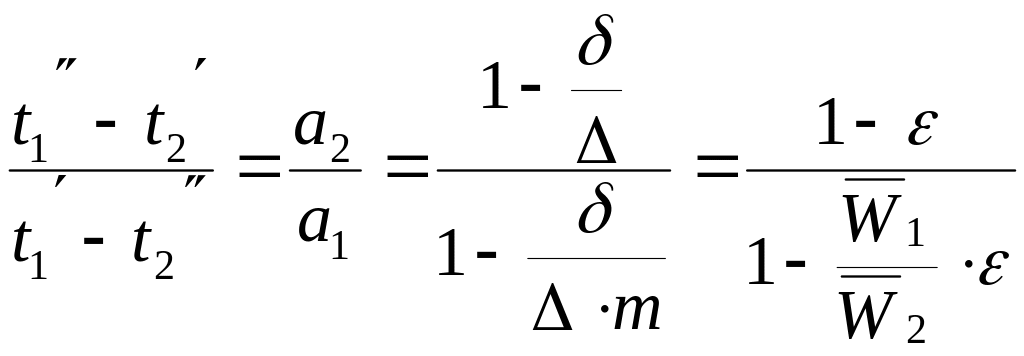 .
(3.11)
.
(3.11)
Решая совместно уравнения (3.9) и (3.11), получаем окончательно выражение для эффективности противоточного теплообменника:
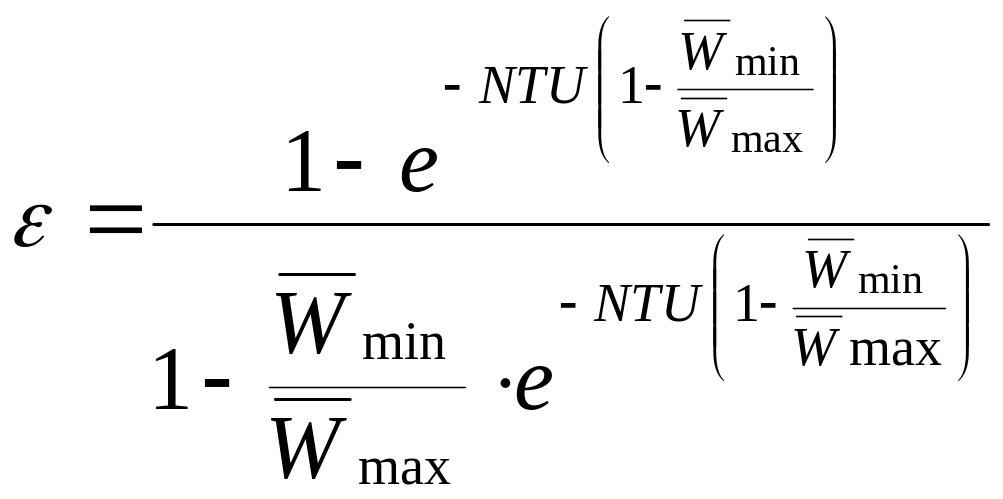 .
(3.12)
.
(3.12)
По этому уравнению построен график (рис. 3.3).
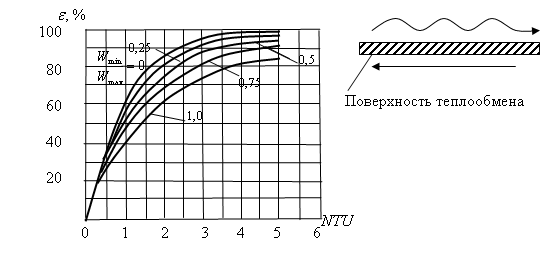
Рис. 3.3 Характеристика противоточного теплообменника
Анализируя
зависимость
![]() ,
можно сделать вывод о том, что меньшее
соотношение водяных эквивалентов
теплоносителей позволяет получить
большую эффективность при заданном
значении NTU.
,
можно сделать вывод о том, что меньшее
соотношение водяных эквивалентов
теплоносителей позволяет получить
большую эффективность при заданном
значении NTU.
Рассмотрим два предельных случая уравнения (3.12).
Если
в процессе передачи тепла одна из
жидкостей имеет постоянную температуру
(происходит процесс кипения жидкости
или конденсации насыщенного пара), то
ее водяной эквивалент бесконечно велик,
т.е.
![]() и при этом
и при этом
![]() .
(3.13)
.
(3.13)
Если
![]() ,
т.е.
,
т.е.
![]() ,
то уравнение (3.12) принимает вид:
,
то уравнение (3.12) принимает вид:
![]() .
(3.14)
.
(3.14)
В случае прямоточного движения теплоносителей эффективность теплообменника рассчитывается по выражению
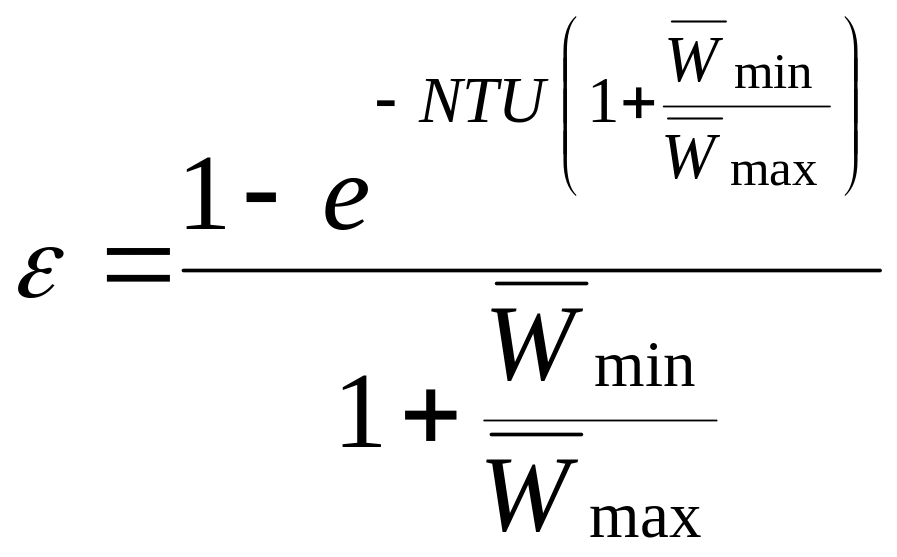 .
(3.15)
.
(3.15)
На рис. 3.4 представлена характеристика прямоточного теплообменника.
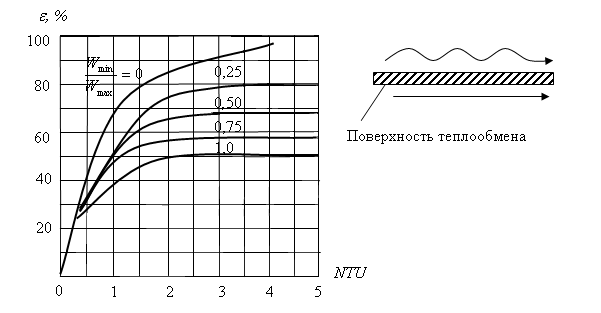
Рис. 3.4 Характеристика прямоточного теплообменника
Из анализа уравнения (3.15) следует, что эффективность прямоточного теплообменника совпадает с эффективностью противоточного теплообменника при . Для другого предельного случая эффективность прямоточного теплообменника составляет лишь 50 % её значения для противотока. При этом уравнение (3.15) приводится к следующему виду:
![]() .
(3.16)
.
(3.16)
В работе [1] приведены аналитические выражения для определения эффективности теплообменников, имеющих более сложные схемы движения теплоносителей.
