Эквипотенциальные поверхности.

Наглядное графическое изображение электростатических полей, возможно, не только с помощью картины силовых линий, дающих представление о напряженности в каждой точке поля, но и с помощью эквипотенциальных поверхностей.

Эквипотенциальная поверхность это множество точек, в которых потенциал имеет одно и то же значение.

Обычно изображают сечение этих поверхностей какой-либо плоскостью (плоскостью чертежа) пунктирными линиями. Для всех точек поверхности выполняется условие . Форма эквипотенциальной поверхности определяется конфигурацией системы зарядов, создающих поле. Для точечного заряда , , если , т.е. эквипотенциальные поверхности представляют собой концентрические сферы с общим центром в точке, где находится создающий поле заряд.

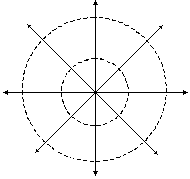
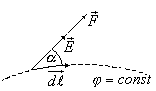
Силовые линии электростатического поля перпендикулярны эквипотенциальным поверхностям. Действительно, если мысленно перемещать пробный заряд по эквипотенциальной поверхности, то работа равна нулю ( ). А это возможно, если сила перпендикулярна перемещению ( , следовательно т.е ).

Вектор градиента потенциала электрического поля. Связь напряженности и градиента потенциала.

При перемещении в поле от исследуемой точки значение потенциала изменяется.

Вектор градиента потенциала электрического поля направлен в сторону увеличения потенциала перпендикулярно к эквипотенциальной поверхности. Отношение бесконечно малого изменения потенциала к бесконечно малому перемещению в этом направлении принимает максимальное значение, а по модулю вектор градиента равен этому отношению.

Математически это можно записать в виде

,

где  — единичный вектор, направленный в сторону увеличения потенциала перпендикулярно к эквипотенциальной поверхности. Единица измерения градиента — В/м.

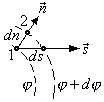
На рис. показаны две эквипотенциальные поверхности, соответствующие потенциалам и . Из рисунка видно что, , т.к. .

Работа сил поля по переносу заряда из точки 1 в точку 2 вдоль нормали равна , учитывая что , получим . Сократив на величину заряда и разделив обе части равенства на величину перемещения , получим связь между напряженностью и градиентом потенциала

.

Из этого соотношения видно, что вектор направлен по нормали к эквипотенциальной поверхности в сторону убывания потенциала, т. е. вектора напряженности поля и градиента потенциала равны по модулю, но противоположны по направлению: .

Градиент и напряженность измеряются в одних и тех же единицах — В/м.

Вектор градиента в декартовых прямоугольных координатах имеет вид: , где частные производные потенциала  по x, y, и z являются проекциями вектора градиента соответственно на оси x, y, z. Используя, векторно-дифференциальный оператор «набла» — , запишем градиент как произведение этого оператора на потенциал , , тогда вектор напряженности электрического поля записывают в виде .

Графическое изображение электрических полей.

Два способа изображения электростатических полей — силовыми линиями и эквипотенциальными поверхностями — эквивалентны: имея одну из этих картин, можно легко построить другую. Особенно наглядны рисунки, на которых изображены обе эти картинки. Густота силовых линий выбирается так, чтобы количество этих линий, пронизывающих единицу поверхности, перпендикулярной к линиям напряженности было равно модулю вектора . Тогда по картине линий напряженности можно судить не только о направлении вектора в разных точках пространства, но и о величине этого вектора. Эквипотенциальные поверхности и силовые линии взаимно перпендикулярны.

Эквипотенциальные поверхности проводят так, чтобы значения потенциалов соседних поверхностей отличались на одно и то же значение, допустим на 1 В ( ). Так как , то . То есть расстояние между соседними эквипотенциальными поверхностями будет тем больше чем меньше E.

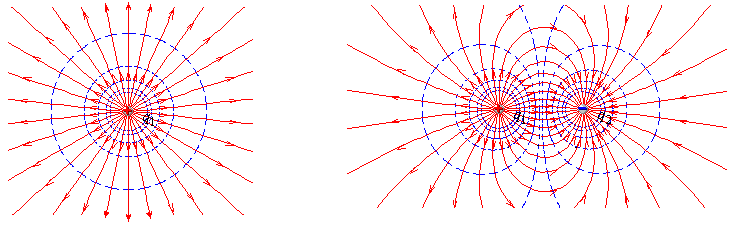
На рисунке изображены поле положительного точечного заряда и поле системы двух точечных разноименных зарядов, по модулю численно равных друг другу. Эквипотенциальные поверхности проведены пунктирными линиями.