
- •Лекция №1
- •Введение
- •Закон сохранения электрического заряда
- •Взаимодействие точечных зарядов. Закон Кулона
- •Электрическое поле. Напряженность электрического поля.
- •Напряженность поля точечного заряда
- •Линии напряженности.
- •Потенциальная энергия пробного заряда в поле точечного заряда (потенциальная энергия системы двух точечных зарядов). Потенциал электрического поля.
- •Работа по перемещению заряда в электрическом поле. Условие потенциальности электрического поля.
- •Эквипотенциальные поверхности.
- •Вектор градиента потенциала электрического поля. Связь напряженности и градиента потенциала.
- •Графическое изображение электрических полей.
- •Поток вектора напряженности электрического поля.
- •Теорема Гаусса
- •Дивергенция векторного поля
- •Теорема Гаусса в дифференциальном виде
- •Применение теоремы Гаусса для расчёта электрических полей
- •Поле бесконечной, равномерно заряженной плоскости
- •Две бесконечные плоскопараллельные разноименно заряженные плоскости
- •Бесконечный равномерно заряженный цилиндр (нить)
- •Два коаксиальных бесконечных равномерно заряженных цилиндра
- •Заряженная сфера
- •Концентрические равномерно заряженные сферы
- •Поле равномерно заряженного шара Принцип суперпозиции полей
- •Электрический диполь. Электрический (дипольный) момент
- •Поле точечного диполя
- •Энергия диполя в поле
- •Момент сил, действующих на диполь. Сила, действующая на диполь в неоднородном поле.
- •Электрическое поле в диэлектриках
- •Механизмы поляризации
- •Поверхностные и объёмные связанные заряды
- •Электростатическое поле в диэлектрике
- •А следовательно, . Таким образом, физической причиной ослабления поля в диэлектрике является поляризация его и появление собственного поля поляризационных связанных зарядов.
- •Вектор электрической индукции (электрического смещения)
- •Связь между векторами и .
- •Поведение векторов и на границе двух сред
- •Сегнетоэлектрики
- •В зависимости от сегнетоэлектрика петля может быть широкой или узкой.
- •Пьезоэлектрики
- •Проводники в электрическом поле
- •Поле заряженного проводника
- •Электроемкость уединенного проводника. Электроемкость проводящего шара
- •Конденсаторы. Емкость конденсаторов
- •Емкость плоского конденсатора
- •Емкость сферического конденсатора
- •Емкость цилиндрического конденсатора
- •Соединение конденсаторов
- •Энергия системы точечных зарядов
- •Энергия заряженного проводника
- •Энергия конденсатора
- •Энергия электрического поля
- •Законы постоянного тока Электрический ток
- •Плотность тока
- •Сторонние силы. Эдс сторонних сил. Напряжение.
- •Закон Ома для однородного участка цепи. Сопротивление проводника.
- •Закон Ома в дифференциальной форме
- •Закон Джоуля — Ленца
- •Закон Ома для замкнутой цепи. Закон Ома для неоднородного участка цепи
- •Разветвленные цепи. Правила Кирхгофа
- •Работа и мощность тока
- •Электронная теория проводимости металлов (классическая теория Друде — Лоренца)
- •Закон Ома в электронной теории
- •Закон Джоуля — Ленца в электронной теории
- •Закон Видемана — Франца в электронной теории
- •Затруднения классической электронной теории металлов
- •Сверхпроводимость
- •Работа выхода электрона из металла Работа, которую нужно затратить для удаления электрона из твердого тела в вакуум, называется работой выхода.
- •Контактная разность потенциалов
- •Термоэлектрические явления и их применение
- •Явление Зеебека.
- •Явление Пельтье.
- •3.Явление Томсона
- •Термоэлектронная эмиссия
- •Квантовая теория. Энергетические состояния электронов в твердых телах. Энергия Ферми
- •Классификация твердых тел по зонной теории
- •Объяснение затруднений классической теории металлов. Как справилась с затруднениями квантовая теория?
- •Полупроводники Собственная проводимость полупроводника
- •Примесная проводимость полупроводников
- •Полупроводник типа n
- •Полупроводник типа p
- •Объяснение p-n перехода с квантовой точки зрения
Объяснение p-n перехода с квантовой точки зрения
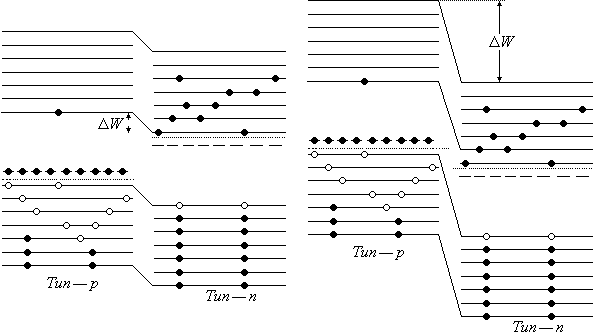
![]() (заряд электрона отрицателен).
Энергетические уровни полупроводника
типа — n опускаются. Полупроводник
типа — p приобретает
отрицательный потенциал. Электроны
этого полупроводника получают
дополнительную положительную энергию
и его энергетические уровни поднимаются.
Этот процесс будет происходить до тех
пор, пока не станут одинаковыми уровни
Ферми обоих кристаллов.
(заряд электрона отрицателен).
Энергетические уровни полупроводника
типа — n опускаются. Полупроводник
типа — p приобретает
отрицательный потенциал. Электроны
этого полупроводника получают
дополнительную положительную энергию
и его энергетические уровни поднимаются.
Этот процесс будет происходить до тех
пор, пока не станут одинаковыми уровни
Ферми обоих кристаллов.
В состоянии равновесия на границе p-n
число переходов электронов слева направо
равно числу переходов справа налево.
Справа электронов много, но им надо
преодолеть потенциальный барьер W
(вероятность перехода пропорциональна
![]() ).
Слева электронов мало, зато они свободно
спускаются с потенциального барьера.
В результате незначительные электронные
токи справа и слева равны. Это же можно
сказать и о дырочных токах.
).
Слева электронов мало, зато они свободно
спускаются с потенциального барьера.
В результате незначительные электронные
токи справа и слева равны. Это же можно
сказать и о дырочных токах.
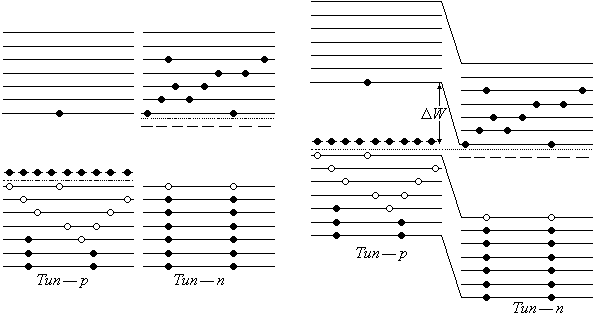
Приложим теперь к p-n
переходу внешнюю разность потенциалов
U так, чтобы на p
— полупроводник подавался положительный
потенциал, а на n —
полупроводник отрицательный, т. е.
внешнее поле направлено против контактного
поля p-n
перехода. Энергетические уровни
n-полупроводника поднимутся,
а p-полупроводника
опустятся. Потенциальный барьер W
уменьшится на
![]() .
Уменьшение потенциального барьера
приведет к резкому увеличению потока
электронов справа налево и дырок слева
направо. Равновесие нарушается. Через
p-n
переход пойдет ток тем более сильный,
чем больше U.
.
Уменьшение потенциального барьера
приведет к резкому увеличению потока
электронов справа налево и дырок слева
направо. Равновесие нарушается. Через
p-n
переход пойдет ток тем более сильный,
чем больше U.
При подключении источника тока в обратном направлении (плюс на n–полупроводник, и минус на p–полупроводник), внешнее поле, по направлению, совпадает с контактным полем p–n перехода. Потенциальный барьер W возрастает, и поток электронов из n в p практически исчезает, а из p в n остается, практически, таким же, что и был в равновесии, очень слабым. Идет слабый ток, создаваемый только не основными носителями тока полупроводников p и n.
___________________________________________________________________
Для решения задач электростатики в неоднородной среде удобно ввести вспомогательную величину — вектор электрического смещения .
![]() .
.
![]() ;
;
![]() ,
т.е.
,
т.е.
![]() .
.
Это значит, что величина не изменяется при переходе границы, в то время как величина меняется скачкообразно.
Линии
вектора
проводятся и определяются так же, как
и линии вектора
.
Величина
![]() называется потоком вектора
.
называется потоком вектора
.
Запишем
теорему Гаусса для напряженности
электрического поля
 .
В среде напряженность в каждой точке
уменьшится в
раз, а следовательно и поток вектора
напряженности будет уменьшен в
раз. Умножая левую и правую части
равенства теоремы Гаусса на
получим теорему Гаусса для потока
вектора
.
В среде напряженность в каждой точке
уменьшится в
раз, а следовательно и поток вектора
напряженности будет уменьшен в
раз. Умножая левую и правую части
равенства теоремы Гаусса на
получим теорему Гаусса для потока
вектора
 ,
,
![]() .
.
Из последнего равенства видно, что [ФD] = Кл, а [D] = Кл/м2.
