Электронная теория проводимости металлов (классическая теория Друде — Лоренца)

Электронная теория металлов была разработана немецким физиком П. Друде и усовершенствована Г. Лоренцем в начале 20-го века.

В классической электронной теории электроны проводимости рассматриваются как электронный газ, подобный идеальному одноатомному газу. Движение электронов подчиняется законам классической механики Ньютона. Взаимодействием электронов между собой пренебрегают, они почти не сталкиваются из-за малого их размера и считают, что они сталкиваются только с положительными ионами решетки. По этой теории электронный газ должен подчиняться всем законам идеального газа. Средняя скорость теплового движения электронов при комнатной температуре примерно равна  м/с.

При включение поля на хаотическое тепловое движение электронов накладывается их упорядоченное движение с некоторой средней скоростью . Величина этой скорости достигает небольших значений порядка  м/с.

Как видим, эта скорость не влияет на среднее время между двумя последовательными соударениями, которое будет равным , где — путь, проходимый электронами между двумя последовательными соударениями, называемый средней длиной свободного пробега.

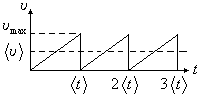
Если внутри металла создано однородное электрическое поле напряженностью , то на электрон действует сила . Эта сила сообщает электрону ускорение направленного движения, определяемое из второго закона Ньютона , где m — масса электрона.

При каждом соударении электрон полностью передает кристаллической решетке приобретенную в электрическом поле энергию и в результате соударения скорость упорядоченного движения опять становится равной нулю. На рисунке приведен график скорости упорядоченного движения электрона от времени t. За время свободного пробега скорость упорядоченного движения возрастает от 0 до , а, учитывая, что , запишем

.

И за этот промежуток времени электрон приобретает кинетическую энергию 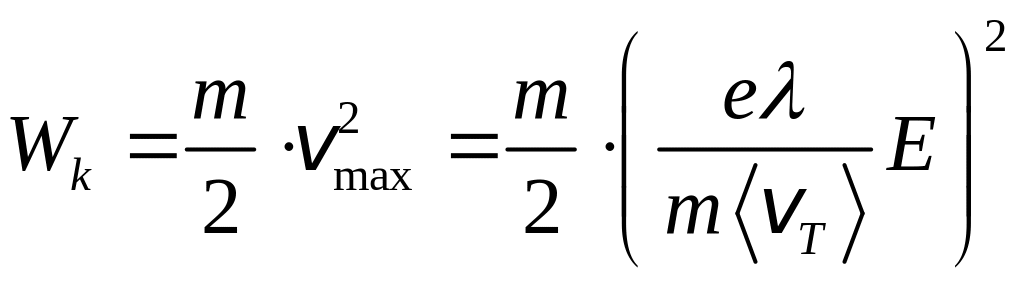,или после сокращения на m:

.

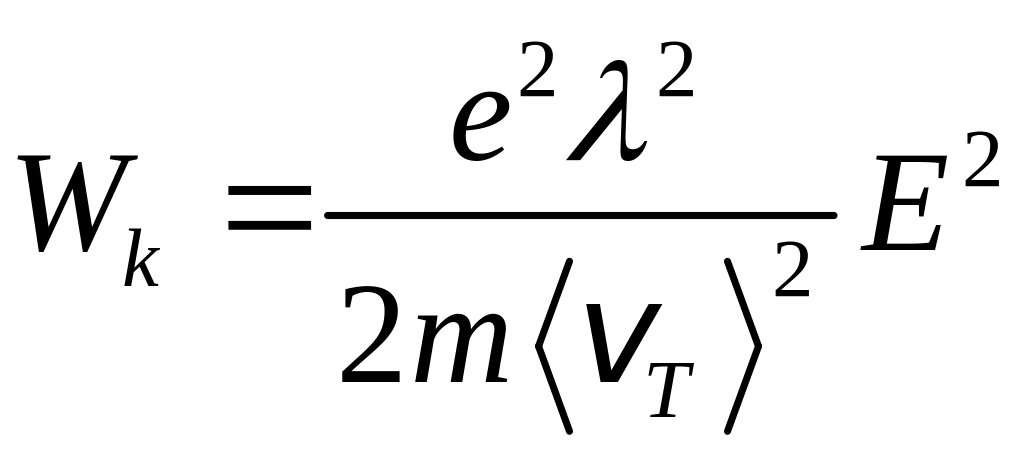Закон Ома в электронной теории

Плотность тока определяется средней скоростью упорядоченного движения электронов , где — концентрация электронов. Средняя скорость упорядоченного движения электронов равна . Тогда

.

Эта формула есть закон Ома в электронной теории Друде — Лоренца, записанный в дифференциальной форме, сопоставив его с уравнением , мы получим:

.

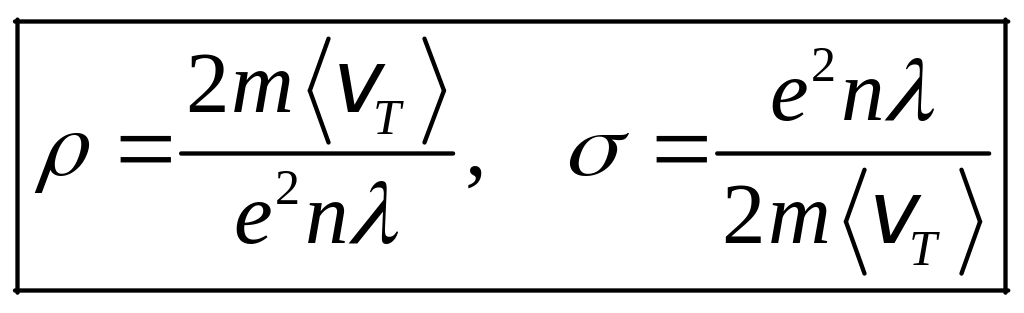Закон Джоуля — Ленца в электронной теории

Энергия, накапливаемая электронами, при столкновениях передается ионам кристаллической решетки. Полная энергия, выделяющаяся в единице объема за среднее время между двумя последовательными соударениями , определится следующим выражением , или 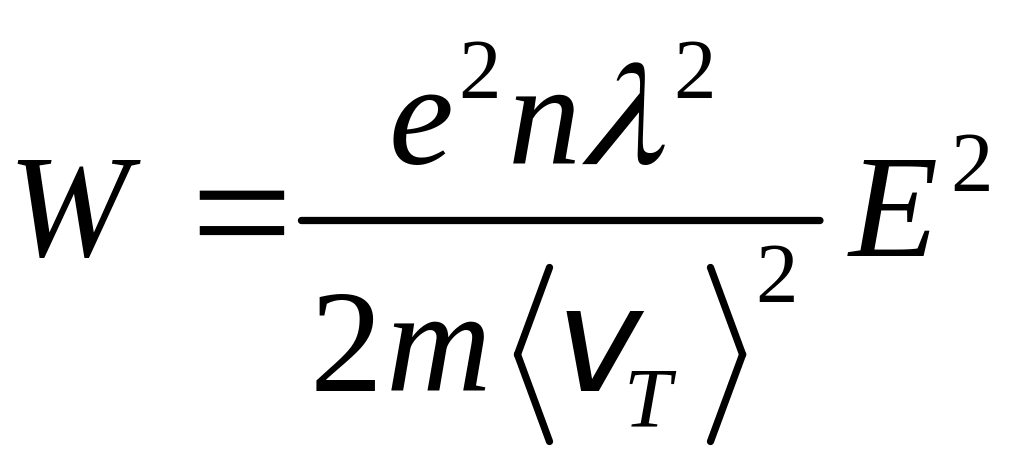. Тогда удельная тепловая мощность будет равна 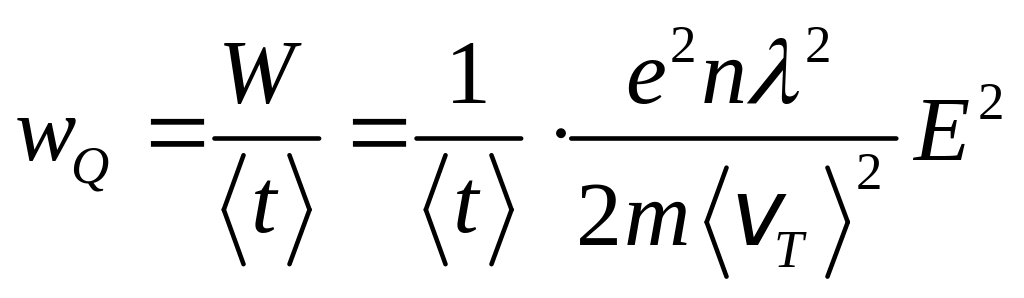и, учитывая, что , запишем 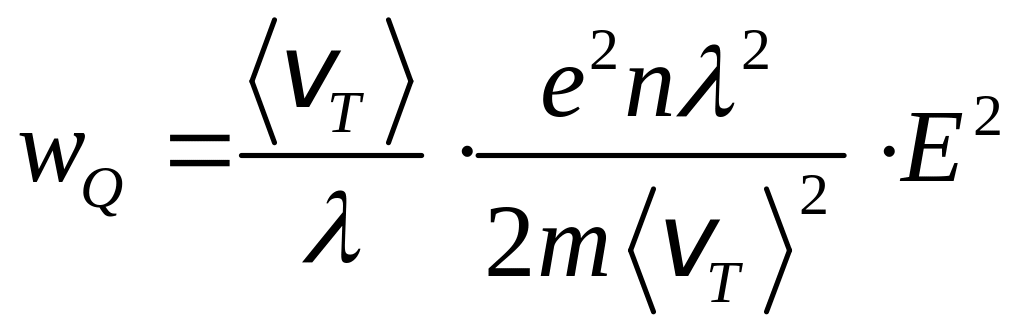. А, после сокращение это выражение принимает вид

.

Эта формула есть закон Джоуля — Ленца в электронной теории Друде — Лоренца, записанный в дифференциальной форме, сопоставив его с уравнением , мы получим такие же значения удельного сопротивления и удельной проводимости , как и в законе Ома электронной теории.

Закон Видемана — Франца в электронной теории

В середине 19-го века Видеман и Франц опытным путем установили, что отношение коэффициента теплопроводности к коэффициенту электропроводности одинаково для всех металлов и линейно возрастает с увеличением температуры:

.

Электронная теория Друде — Лоренца качественно объясняет и этот закон. «Газ» свободных электронов по своим тепловым свойствам подобен одноатомному идеальному газу с числом степеней . Поэтому мы можем воспользоваться известной формулой молекулярно-кинетической теории для коэффициента теплопроводности

,

где — плотность «газа» свободных электронов, — удельная теплоемкость электронного «газа» при постоянном объеме. Учитывая, что , запишем , где R — универсальная газовая постоянная; — молярная масса «газа» свободных электронов, k — постоянная Больцмана. Подставляя и в формулу теплопроводности, получим

.

Найдем теперь отношение коэффициентов теплопроводности к электропроводности, 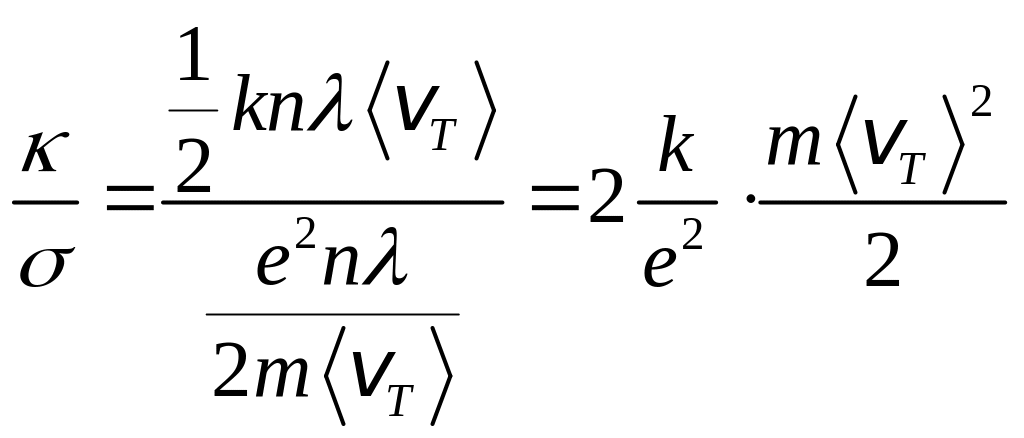но , поэтому

.

Друде получил отношение, хорошо согласующееся с опытом. Лоренц, желая улучшить результат, предположил, что скорости свободных электронов распределены по закону Больцмана. При таком предположении в отношении вместо коэффициента «3» появляется «2», что плохо согласуется с опытом. При истолковании закона Видемана — Франца теория столкнулась с серьезным затруднением. Это затруднение было не единственным.