Закон Ома для замкнутой цепи. Закон Ома для неоднородного участка цепи

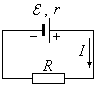
Рассмотрим замкнутую электрическую цепь, содержащую источник тока с ЭДС и внутренним сопротивлением r и нагрузку, характеризуемую только сопротивлением (см. рисунок). Сопротивление соединительных проводов будем считать равным нулю. Заряды, перемещаясь по цепи, передают энергию электрического поля в виде теплоты. Однако эта потеря энергии полностью возмещается работой сторонних сил .

По закону Джоуля — Ленца , где — сопротивление всей цепи. Работа сторонних сил равна , где — перемещаемый заряд. Тогда . Принимая во внимание что, , после сокращения получим закон Ома для замкнутой цепи

, или

.

Рассмотрим неоднородный участок цепи, между концами которого существует некоторая разность потенциалов и внутри которого включен источник тока с ЭДС, равной . На носители тока на таком участке кроме сил электростатического поля будут действовать еще сторонние силы. На таком участке цепи, выделяющаяся теплота численно равна работе, совершаемой электростатическими и сторонними силами .

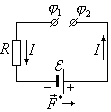
По закону Джоуля — Ленца , где — сопротивление всего участка цепи. По определению разности потенциалов , где , определим работу электростатических сил . Работа сторонних сил равна , где — перемещаемый заряд. На участке цепи, изображенном на рисунке сторонние силы направлены в ту же сторону, что и электростатические, т. е. в сторону движения положительных зарядов. Тогда

(1)

Принимая во внимание что, , после сокращения получим закон Ома для неоднородного участка цепи

. (2)

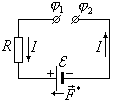
На участке цепи, в котором сторонние силы направлены против тока (в сторону противоположную движения положительных зарядов), энергия электрического поля переходит не только в теплоту, но и в другие виды энергии, например, запасается энергия в химических процессах при зарядке аккумулятора (см. рисунок). В этом случае, работа сторонних сил принимает отрицательное значение , а уравнение (1) принимает вид

.

После сокращения левой части на , а правой на , получим закон Ома уже для этого неоднородного участка цепи

. (3)

Приступая к анализу неоднородного участка цепи, мы можем вообще не задумываться о том, в какую сторону течет ток на самом деле, а задавать ему направление произвольно. Тогда при написании закона Ома для неоднородного участка цепи

необходимо соблюдать правило знаков. Направление обхода участка цепи задает индексация у потенциалов: в уравнениях (2) и (3) от конца участка с потенциалом к концу участка с потенциалом . Если направление тока совпадает, с направлением обхода, то падение напряжения берется со знаком плюс, не совпадает — со знаком минус. Если действие сторонних сил совпадает с направлением обхода (переходим с «–» полюса на полюс «+»), то ЭДС берется со знаком плюс, не совпадает (переходим с «+» полюса на полюс «–»), то ЭДС берется со знаком минус.

Умножив уравнения (2) и (3) на –1

, (4)

, (5)

мы тем самым изменили направление обхода. Направление обхода стало: от конца участка с потенциалом к концу участка с потенциалом , и уравнения (4) и(5) написаны в полном соответствии с правилом знаков.

Очевидно, закон Ома в дифференциальной форме для неоднородного участка цепи будет иметь вид

,

кроме электростатических сил на носители тока действуют сторонние силы.