Электрическое поле. Напряженность электрического поля.

Взаимодействие между электрическими зарядами осуществляется через их электрические поля, а именно, электрическое поле 1-го заряда действует на второй и наоборот, электрическое поле 2-го заряда действует на первый.

Всякий заряд изменяет свойства окружающего его пространства — создает в нем электрическое поле. Поля, которые создаются неподвижными электрическими зарядами, называются электростатическими. Для обнаружения и опытного исследования электростатического поля используется пробный точечный заряд — такой заряд, который своим действием не искажает исследуемое поле (не вызывает перераспределение зарядов, создающих поле). Отношение силы , действующей на пробный заряд со стороны поля к величине пробного заряда , не зависит от величины этого пробного заряда и характеризует данную точку поля. То есть, если увеличить величину пробного заряда в 5 раз, то и сила, действующая на пробный заряд, увеличится в 5 раз, а отношение останется неизменным. Это отношение определяет физическую величину, называемую напряженностью электростатического поля, которую мы обозначим :

.

Если в этой формуле положить , то по величине и направлению совпадает с силой . Таким образом, напряженность электростатического поля в некоторой точке является физической величиной, численно равной силе, действующей на единицу положительного заряда, помещенного в эту точку, и имеющей направление этой силы. Из этого определения, следует, что напряженность есть величина векторная.

Напряженность поля точечного заряда

Возьмем точечный заряд q и определим напряженность поля в произвольной точке, отстоящей от заряда на расстоянии r.

По закону Кулона сила , действующая на положительный пробный заряд q_пр, помещенный на расстоянии r от заряда q, равна:

.

Отсюда напряженность поля, в заданной точке будет: .

,

где — радиус-вектор, проведенный от того места, где расположен точечный заряд q, к тому месту, в котором вычисляется напряженность поля . Или в скалярной форме

.

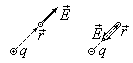
Вектор во всех точках поля направлен радиально от заряда, если он положителен, и радиально к заряду, если отрицателен.

Линии напряженности.

Графически электростатическое поле изображают с помощью линий напряженности (силовых линий). Под линией напряженности будем подразумевать такую линию, в каждой точке которой вектор напряженности направлен по касательной к этой линии.

Так как в каждой точке пространства вектор напряженности имеет лишь одно направление, то линии напряженности никогда не пересекаются. Для однородного поля ( ) линии напряженности параллельны вектору .

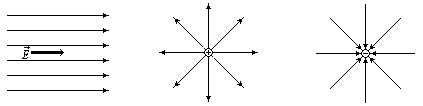
Линии напряженности точечного заряда — это прямые линии, выходящие из заряда, если он положительный, и входящие в заряд, если он отрицательный. Таким образом, положительный заряд можно рассматривать как место начала линий напряженности (источники поля), а отрицательный заряд — как место окончания линий напряженности (стоки поля). Касательные к линиям напряженности в обоих этих случаях совпадают с самими линиями и направлены в каждой точке в том же направлении, что и напряженность.

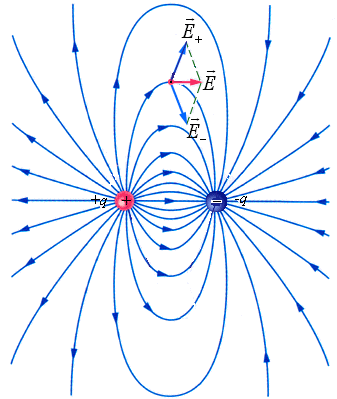
Представим на рис. линии напряженности двух точечных разноименных зарядов, по модулю численно равных друг другу.