Емкость цилиндрического конденсатора

Цилиндрический конденсатор образуется двумя коаксиальными проводящими цилиндрами. Пусть радиусы внутренней и внешней обкладок конденсатора равны соответственно и . Длинна, конденсатора равна . Заряд конденсатора , где — линейная плотность заряда. Напряженность поля между обкладками определяется выражением , а напряжение

.

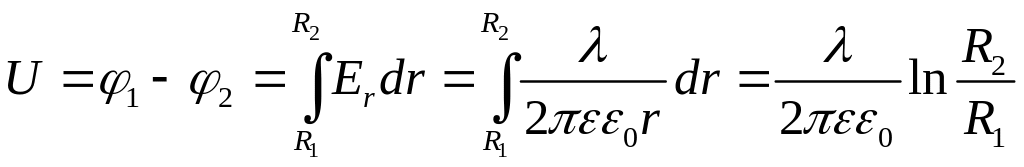Отсюда емкость цилиндрического конденсатора будет равна ,

.

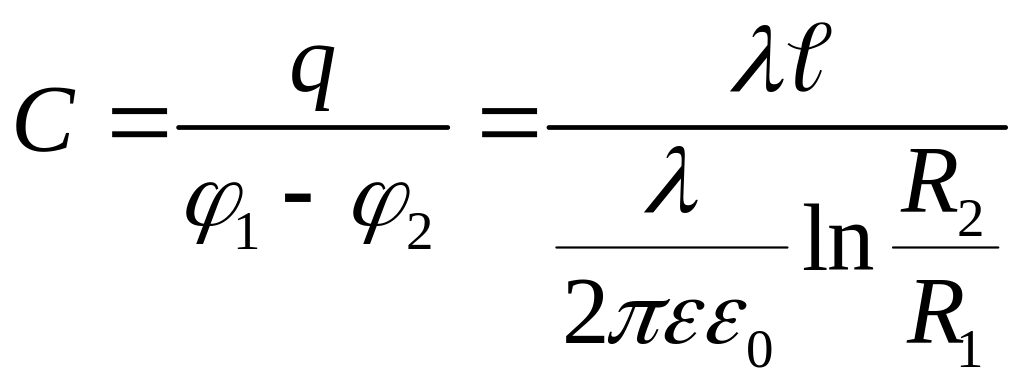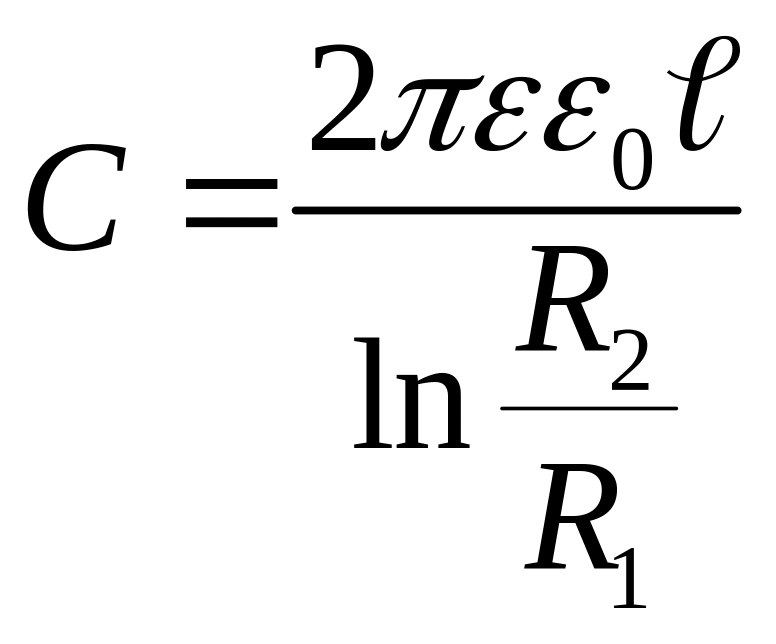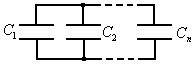
Соединение конденсаторов

При параллельном соединении конденсаторов емкости складываются:

.

При последовательном соединении складываются обратные величины емкостей:

.

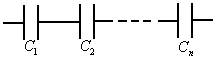
Энергия системы точечных зарядов

Энергия взаимодействия системы точечных зарядов определяется работой, которую совершают силы взаимодействия между зарядами при удалении их относительно друг друга на бесконечно большие расстояния.

Сначала рассмотрим систему из двух точечных зарядов и . Как мы уже доказали ранее потенциальная энергия взаимодействия этих зарядов равна

.

Каждый заряд взаимодействует с полем другого заряда. Введем обозначения: — потенциал поля, создаваемого вторым зарядом в месте нахождения первого заряда; — потенциал поля, создаваемого первым зарядом в месте нахождения второго заряда. Тогда потенциальную энергию взаимодействия двух точечных зарядов можно записать в следующем виде , или в симметричном виде

.

Обобщим полученное выражение на систему из произвольного числа зарядов. Энергия взаимодействия системы точечных зарядов

,

где — потенциал, создаваемый в месте нахождения i-го заряда всеми остальными зарядами системы.

Энергия заряженного проводника

Заряды проводника образуют систему. Энергия системы зарядов равна . Поскольку значение во всех точках, где имеются заряды, одинаково, можно вынести за знак суммы. Тогда оставшаяся сумма есть не что иное, как заряд на проводнике, и

.

Эти выражения записаны с учетом того, что .

Энергия конденсатора

Пусть — заряд конденсатора, — потенциал положительно заряженной обкладки конденсатора, — потенциал отрицательно заряженной обкладки конденсатора. Заряды конденсатора представляют собой систему зарядов, энергия которой определится формулой . Приняв во внимание, что , где — разность потенциалов на обкладках, получим следующие выражения для энергии конденсатора

.

Здесь надо заметить, что эти формулы определяют полную энергию взаимодействия: не только энергию взаимодействия зарядов одной обкладки с зарядами другой, но и энергию взаимодействия зарядов внутри каждой обкладки.

Энергия электрического поля

Энергию заряженного конденсатора можно выразить через величину, характеризующую электрическое поле — через напряженность . Убедимся в этом сначала на простейшем примере плоского конденсатора. Подстановка в формулу выражения дает . Умножив и числитель и знаменатель правой части этого равенства на d, получим . А поскольку и (объем между обкладками конденсатора), то

.

Эта формула подводит к физической идее о локализации энергии в самом поле. Данное предположение нашло опытное подтверждение в области переменных во времени полей. Электромагнитные волны переносят энергию, — уже это заставляет нас признать, что носителем энергии является само поле.

Полученная формула справедлива для однородного поля конденсатора, заполняющего объем . Из нее следует, что электрическая энергия распределена в пространстве с объемной плотностью

.

В более строгом курсе физики доказывается, что формула объемной плотности энергии справедлива не только для однородного поля, но и для любого не однородного поля, изменяющегося во времени . Тогда энергию неоднородного поля можно найти интегрированием

по объему, занимаемым полем.