Электроемкость уединенного проводника. Электроемкость проводящего шара

Рассмотрим произвольный проводник, удаленный от других проводников, тел и зарядов. Между зарядом такого проводника и его потенциалом существует прямая пропорциональность: . Следовательно, не зависит от заряда , для каждого уединенного проводника это отношение имеет свое значение. Величину

называют электроемкостью уединенного проводника (емкостью). Она численно равна заряду, сообщенному проводнику повышающего его потенциал на единицу. Емкость зависит от размеров и формы проводника. Так для проводящего шара, как это мы уже доказали зависимость между зарядом и потенциалом имеет вид . Тогда емкость шара, очевидно будет равна

.

За единицу емкости принимают емкость такого проводника, потенциал которого изменяется на 1 В при сообщении ему заряда 1 Кл. Эту единицу емкости называют фарад (Ф).

Конденсаторы. Емкость конденсаторов

Если проводник не уединен, то его емкость будет существенно увеличиваться при приближении к нему других тел. Это обусловлено тем, что поле данного проводника вызывает перераспределение зарядов на окружающих телах — появление индуцированных зарядов. Пусть заряд проводника . Тогда отрицательные индуцированные заряды оказываются ближе к проводнику, нежели положительные. Поэтому потенциал проводника, являющийся алгебраической суммой потенциалов собственных зарядов и зарядов, индуцированных на других телах, уменьшится при приближении к нему других незаряженных тел. А значит его емкость увеличится.

Это позволило создать систему проводников, которая обладает емкостью, значительно большей, чем уединенный проводник, и притом не зависящей от окружающих тел. Такую систему называют конденсатором. Простейший конденсатор состоит из двух проводников (обкладок), расположенных на малом расстоянии друг от друга, отделенных диэлектрической средой.

Под емкостью конденсатора понимают отношение заряда конденсатора к разности потенциалов между обкладками

.

Разность потенциалов называют напряжением. Естественно, емкость конденсатора измеряют также в фарадах. Емкость конденсатора зависит от размеров и формы обкладок, от зазора между ними и от заполняющей конденсатор диэлектрической среды.

Найдем выражения для емкости некоторых конденсаторов.

Емкость плоского конденсатора

Этот конденсатор состоит из двух параллельных пластин площадью S каждая, разделенных зазором шириной d. Между пластинами находится диэлектрик с относительной проницаемостью равной . Заряд конденсатора , где — поверхностная плотность заряда. Напряженность поля между его обкладками , тогда разность потенциалов . Следовательно, емкость плоского конденсатора будет равна . То есть

.

Емкость реального плоского конденсатора определяется полученным выражением тем точнее, чем меньше зазор d по сравнению с линейными размерами пластин.

Емкость сферического конденсатора

Сферический конденсатор представляет собой две проводящие концентрические сферы. Пусть радиусы внутренней и внешней обкладок конденсатора равны соответственно и . Если заряд конденсатора q, то напряженность поля между обкладками определяется выражением , а напряжение

.

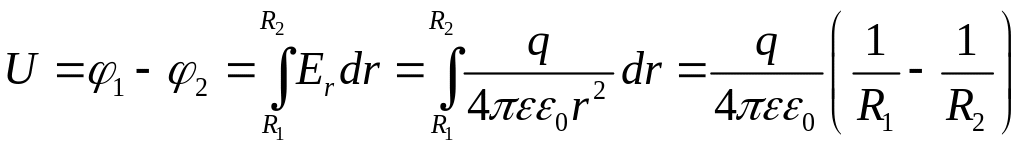Отсюда емкость сферического конденсатора будет равна ,

.
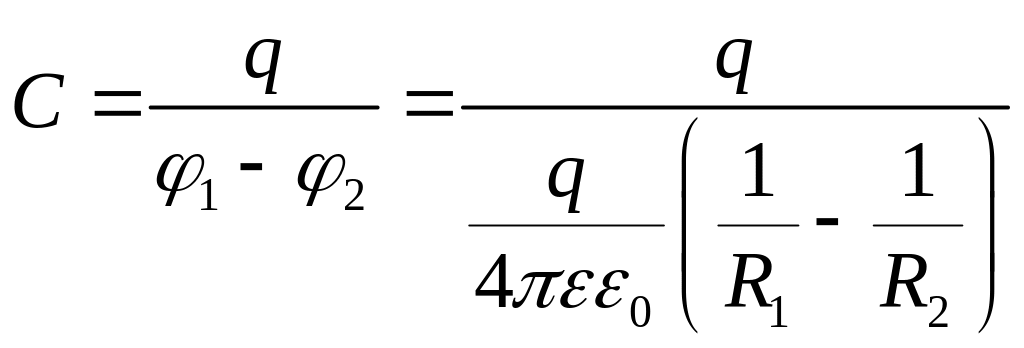