
- •Лекция №1
- •Введение
- •Закон сохранения электрического заряда
- •Взаимодействие точечных зарядов. Закон Кулона
- •Электрическое поле. Напряженность электрического поля.
- •Напряженность поля точечного заряда
- •Линии напряженности.
- •Потенциальная энергия пробного заряда в поле точечного заряда (потенциальная энергия системы двух точечных зарядов). Потенциал электрического поля.
- •Работа по перемещению заряда в электрическом поле. Условие потенциальности электрического поля.
- •Эквипотенциальные поверхности.
- •Вектор градиента потенциала электрического поля. Связь напряженности и градиента потенциала.
- •Графическое изображение электрических полей.
- •Поток вектора напряженности электрического поля.
- •Теорема Гаусса
- •Дивергенция векторного поля
- •Теорема Гаусса в дифференциальном виде
- •Применение теоремы Гаусса для расчёта электрических полей
- •Поле бесконечной, равномерно заряженной плоскости
- •Две бесконечные плоскопараллельные разноименно заряженные плоскости
- •Бесконечный равномерно заряженный цилиндр (нить)
- •Два коаксиальных бесконечных равномерно заряженных цилиндра
- •Заряженная сфера
- •Концентрические равномерно заряженные сферы
- •Поле равномерно заряженного шара Принцип суперпозиции полей
- •Электрический диполь. Электрический (дипольный) момент
- •Поле точечного диполя
- •Энергия диполя в поле
- •Момент сил, действующих на диполь. Сила, действующая на диполь в неоднородном поле.
- •Электрическое поле в диэлектриках
- •Механизмы поляризации
- •Поверхностные и объёмные связанные заряды
- •Электростатическое поле в диэлектрике
- •А следовательно, . Таким образом, физической причиной ослабления поля в диэлектрике является поляризация его и появление собственного поля поляризационных связанных зарядов.
- •Вектор электрической индукции (электрического смещения)
- •Связь между векторами и .
- •Поведение векторов и на границе двух сред
- •Сегнетоэлектрики
- •В зависимости от сегнетоэлектрика петля может быть широкой или узкой.
- •Пьезоэлектрики
- •Проводники в электрическом поле
- •Поле заряженного проводника
- •Электроемкость уединенного проводника. Электроемкость проводящего шара
- •Конденсаторы. Емкость конденсаторов
- •Емкость плоского конденсатора
- •Емкость сферического конденсатора
- •Емкость цилиндрического конденсатора
- •Соединение конденсаторов
- •Энергия системы точечных зарядов
- •Энергия заряженного проводника
- •Энергия конденсатора
- •Энергия электрического поля
- •Законы постоянного тока Электрический ток
- •Плотность тока
- •Сторонние силы. Эдс сторонних сил. Напряжение.
- •Закон Ома для однородного участка цепи. Сопротивление проводника.
- •Закон Ома в дифференциальной форме
- •Закон Джоуля — Ленца
- •Закон Ома для замкнутой цепи. Закон Ома для неоднородного участка цепи
- •Разветвленные цепи. Правила Кирхгофа
- •Работа и мощность тока
- •Электронная теория проводимости металлов (классическая теория Друде — Лоренца)
- •Закон Ома в электронной теории
- •Закон Джоуля — Ленца в электронной теории
- •Закон Видемана — Франца в электронной теории
- •Затруднения классической электронной теории металлов
- •Сверхпроводимость
- •Работа выхода электрона из металла Работа, которую нужно затратить для удаления электрона из твердого тела в вакуум, называется работой выхода.
- •Контактная разность потенциалов
- •Термоэлектрические явления и их применение
- •Явление Зеебека.
- •Явление Пельтье.
- •3.Явление Томсона
- •Термоэлектронная эмиссия
- •Квантовая теория. Энергетические состояния электронов в твердых телах. Энергия Ферми
- •Классификация твердых тел по зонной теории
- •Объяснение затруднений классической теории металлов. Как справилась с затруднениями квантовая теория?
- •Полупроводники Собственная проводимость полупроводника
- •Примесная проводимость полупроводников
- •Полупроводник типа n
- •Полупроводник типа p
- •Объяснение p-n перехода с квантовой точки зрения
Механизмы поляризации
Центры тяжести положительных и отрицательных зарядов в молекуле диэлектрика могут совпадать, например, в молекуле водорода, или не совпадать, например, в молекуле воды. В первом случае молекула называется неполярной, во втором — полярной.
Наличие у молекул постоянных дипольных моментов постулировал немецкий физик Дебай. В честь этого ученого названа внесистемная единица дипольного момента «Дебай» 1 Дебай = 3,33·10-30 Кл·м.
Существуют три основных механизма поляризации: электронный; ионный и ориентационный.
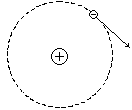
В неполярных молекулах главную роль играет первый из трёх названных механизмов. Простейший пример такой системы — атом водорода.
![]() усреднённый дипольный электрический
момент молекулы
усреднённый дипольный электрический
момент молекулы
![]() ,
(центр тяжести положительного заряда
совпадает с центром тяжести отрицательного).
,
(центр тяжести положительного заряда
совпадает с центром тяжести отрицательного).
При
![]() заряды перераспределяются, электронные
орбиты деформируются, и центры тяжести
зарядов смещаются на некоторое расстояние
друг от друга. Возникает индуцированный
полем электрический момент, пропорциональный
напряжённости поля
:
заряды перераспределяются, электронные
орбиты деформируются, и центры тяжести
зарядов смещаются на некоторое расстояние
друг от друга. Возникает индуцированный
полем электрический момент, пропорциональный
напряжённости поля
:
![]() ,
(1)
,
(1)
где
![]() — электронная
поляризуемость молекулы,
— электрическая
постоянная, появившаяся здесь из
соображений размерности. Вектор
поляризации
— электронная
поляризуемость молекулы,
— электрическая
постоянная, появившаяся здесь из
соображений размерности. Вектор
поляризации
![]() ,
где N — число
молекул в объёме
,
n0 — концентрация
молекул (число молекул в единице объёма).
С учетом (1) получим:
,
где N — число
молекул в объёме
,
n0 — концентрация
молекул (число молекул в единице объёма).
С учетом (1) получим:
![]() .
Безразмерная величина
.
Безразмерная величина
![]() — называется
диэлектрической восприимчивостью.
— называется
диэлектрической восприимчивостью.
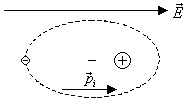
Ионный
механизм имеет место в молекулах с
ионной связью. Внешнее поле стремится
сдвинуть ионы друг относительно друга.
Это также приводит к появлению
индуцированного полем электрического
момента, пропорциональному полю:
![]() ,
где
,
где
![]() — ионная
диэлектрическая восприимчивость. Вектор
поляризации в таких диэлектриках
складывается из электронной и ионной
части:
— ионная
диэлектрическая восприимчивость. Вектор
поляризации в таких диэлектриках
складывается из электронной и ионной
части:
![]() .
Для обычных температур
.
Для обычных температур
![]() не зависят от T.
не зависят от T.
![]() .
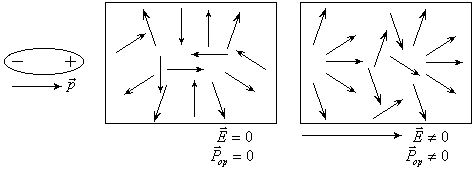
Понятно, что при ориентационном механизме
поляризации восприимчивость
.
Понятно, что при ориентационном механизме
поляризации восприимчивость
![]() должна сильно зависеть от температуры,
что и наблюдается на опыте. Классическую
теорию ориентационной поляризации
создал французский физик Ланжевен в
начале 20 века. При ориентационном
механизме поляризации имеется два
конкурирующих фактора: электрическое
поле, ориентирующее элементарные диполи
— упорядочивающий фактор, и тепловое
движение — дезориентирующий фактор.
Учет этих факторов дает следующий
результат
должна сильно зависеть от температуры,
что и наблюдается на опыте. Классическую
теорию ориентационной поляризации
создал французский физик Ланжевен в
начале 20 века. При ориентационном
механизме поляризации имеется два
конкурирующих фактора: электрическое
поле, ориентирующее элементарные диполи
— упорядочивающий фактор, и тепловое
движение — дезориентирующий фактор.
Учет этих факторов дает следующий
результат
![]() .
.
Если действуют все три механизма, то
![]() ,
где
,
где
![]() — диэлектрическая
восприимчивость. Измерив экспериментально
— диэлектрическая
восприимчивость. Измерив экспериментально
![]() можно разделить разные компоненты
восприимчивости. Такие измерения могут
дать ценную информацию о структуре
молекул.
можно разделить разные компоненты
восприимчивости. Такие измерения могут
дать ценную информацию о структуре
молекул.
Поверхностные и объёмные связанные заряды
Заряды, которые находятся в пределах диэлектрика, но не входят в состав его молекул, а также заряды расположенные за пределами диэлектрика будем называть сторонними.
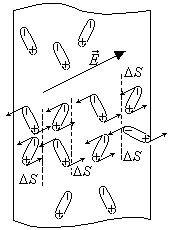
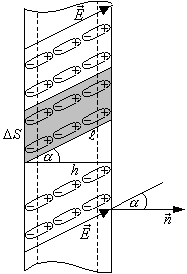
Поляризация сопровождается возникновением в тонком поверхностном слое диэлектрика избытка связанных зарядов одного знака, если только нормальная составляющая электрического поля En к данному участку поверхности отлична от нуля. Под действием этого поля заряды одного знака уходят внутрь, а другого знака выходят к поверхности.
![]() .
.
В тех местах, где линии выходят из диэлектрика на поверхности выступят положительные связанные заряды, там же где линии входят в диэлектрик появятся отрицательные поверхностные заряды.
Определим этот заряд и поверхностную
плотность, выступивших связанных зарядов
![]() .
Выделим, мысленно в пластине элементарный
объём в виде тонкого цилиндра с образующими
параллельными напряженности поля в
диэлектрике
с площадью основания S
(на рисунке он затемнен). Объём цилиндра
.
Выделим, мысленно в пластине элементарный
объём в виде тонкого цилиндра с образующими
параллельными напряженности поля в
диэлектрике
с площадью основания S
(на рисунке он затемнен). Объём цилиндра
![]() .
Электрический момент цилиндра, по
определению вектора поляризации равен:
.
Электрический момент цилиндра, по
определению вектора поляризации равен:
![]() .
(1)
.
(1)
С другой точки
зрения рассматриваемый цилиндр
эквивалентен диполю электрический
момент, которого равен произведению
заряда диполя на плечо (расстояние между
зарядами): ![]() . (2)
. (2)
Приравняв правые части равенств
(2) и (1)
![]() ,
и сократив на
,
и сократив на
![]() ,
получим:
,
получим:
![]() (3)
(3)
То есть, при включении электрического поля через произвольную площадку внутри диэлектрика (в том числе и у поверхности диэлектрика) в направлении поля переносится на микроскопические расстояния связанный заряд , равный потоку вектора поляризации через эту площадку. На поверхности диэлектрика выступят связанные заряды с поверхностной плотностью равной
![]() . (4)
. (4)
Поверхностная плотность
связанных зарядов равна нормальной
составляющей вектора поляризации.
Учитывая, что
![]() запишем (4) в следующем виде
запишем (4) в следующем виде
![]() . (5)
. (5)
Равенства (3), (4)и (5) справедливы в самом общем случае, когда неоднородный диэлектрик произвольной формы находится в неоднородном электрическом поле. В этом случае под Pn и En понимают нормальные составляющие векторов в непосредственной близости от рассматриваемой точки поверхности внутри диэлектрика.
![]() .
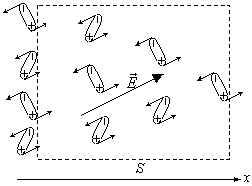
В результате, если диэлектрик окажется
неоднородными, в объёме, ограниченном
поверхностью S возникнет
избыточный связанный заряд (см. рисунок,
внутрь объема войдет заряда больше, чем
выйдет)
.
В результате, если диэлектрик окажется
неоднородными, в объёме, ограниченном
поверхностью S возникнет
избыточный связанный заряд (см. рисунок,
внутрь объема войдет заряда больше, чем
выйдет)
![]() , (6)
, (6)
где
![]() — объёмная
плотность связанного заряда.
— объёмная
плотность связанного заряда.
Поток вектора поляризации через замкнутую поверхность будет равен:
![]() . (7)
. (7)
Применяя
математическую теорему Остроградского
Гаусса для потока вектора поляризации
![]() и сравнивая с уравнением (6) получим:
и сравнивая с уравнением (6) получим:
![]() .
Применим, оператор «набла» и запишем:
.
Применим, оператор «набла» и запишем:
![]() .
С учетом, того что,
.
С учетом, того что,
![]() найдем
найдем
![]() .
После действий с оператором «набла»
получим:
.
После действий с оператором «набла»
получим:
![]() .
.
