Методы понижения дисперсии

Используя компьютер для расчетов, нельзя слепо доверять машине – в некоторых случаях прямое вычисление результатов просто невозможно, или невыгодно. Чтобы побороть эту проблему, были созданы так называемые методы понижения дисперсии. Цель каждого такого метода – промоделировать поведение частиц в неком заданном направлении, при этом пропуская неважные или неинтересные для расчета зоны.

Результаты расчетов методом Монте-Карло подвержены погрешностям не только из-за стохастической природы метода. Одна из основных задач – минимизировать эти погрешности и оценить достоверность полученных в результате расчета данных. Кроме статистических погрешностей, необходимо также учитывать неабсолютную точность табулированных значений сечений и погрешности, вызываемые несовершенностями математических моделей, интерпретирующих геометрию зоны.

Существует несколько способов учета погрешностей:

Статистические тесты:

Предположим, что в ходе расчета мы промоделировали M-событий, и соответственно получили - последовательность искомых величин в случайном порядке. Тогда искомое среднее значение находится по формуле

Усиленный закон больших чисел гласит, что при , при условии, что – конечная величина. Дисперсия в таком случае равна:

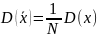
Относительная погрешность в итоге равна:

– это среднеквадратичное отклонение величины . Таблица (X_X) показывает, как эту относительную погрешность необходимо оценивать пользователю. Это ошибка, которая должна и может быть минимизирована с наименьшими затратами машинного времени.

Предел R	Оценка результата
> 0.5	Не имеет смысла
От 0.2 до 0.5	Маловероятно
От 0.1 до 0.2	Сомнительно
<0.1	Достоверно, за исключением точечного/кольцевого детектора
<0.05	Как правило, достоверно
Таблица (X_X)

Значение R определяется двумя величинами - эффективностью подсчета историй q (долей историй, которая внесла ненулевой вклад в подсчеты), и разбросом ненулевых данных. Для подсчетов, обусловленных не засчитываемыми событиями, функция распределения вероятности p(x) имеет пик погрешности при x=0. Потому MCNP делит погрешность на две составляющие

где первая составляющая представляет собой неэффективность подсчета, а вторая – собственное распределение ненулевых событий из всех учитываемых. Если =0 при (каждая частица вносит полезный вклад), то желательно увеличить эффективность подсчета настолько, насколько это возможно, в то же время сужая разброс 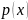вокруг , чтобы увеличить . Это и есть цель использования методов понижения дисперсии, описанных выше.

Другие статистические показатели:

Уровень надежности

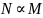Где T – время симуляции, которое обычно пропорционально количеству N промоделированных историй. При и , должен оставаться на примерно постоянном уровне все активные циклы симуляции. Ясно, что желателен большой , так как это приводит к получению результатов с нужной нам степенью погрешности за меньшее расчетное время.