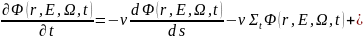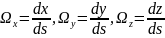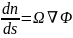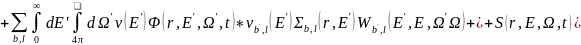1) Баланс нейтронов в размножающей среде
Уравнение переноса нейтронов есть одночастичное уравнение Больцмана, так как по сравнению с плотностью вещества в среде, плотность нейтронного газа в ней достаточно мала, вследствие чего можно пренебречь влиянием распределения нейтронов по скоростям на аналогичное распределение ядер вещества, а так же соударениями нейтронов друг с другом.
|
(1.1) |
(1)
есть распределение нейтронов в момент
времени t
в некоем пространстве с координатами
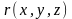 ,
по энергии E
и по направлениям скоростей движения
нейтронов
,
по энергии E
и по направлениям скоростей движения
нейтронов
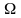 .
.
Отсюда
видно, что
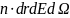 есть
число нейтронов в элементе объема dr
c
энергией
есть
число нейтронов в элементе объема dr
c
энергией
 ,
и с направлением скоростей движения
вдоль орта
,
и с направлением скоростей движения
вдоль орта
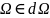 .
.
Среда, в которой осуществляется перенос нейтронов, обладает макроскопическими сечениями взаимодействия для нейтронов
|
(1.2) |
где
b
означает тип взаимодействия (a
– поглощение нейтронов, f
– деление ядра нейтроном, se
– упругое рассеяние, si
– неупругое рассеяние, t
– полное сечение взаимодействия равное
 и т. д.)
и т. д.)
 – ядерная плотность l-того
изотопа в точке r,
– ядерная плотность l-того
изотопа в точке r,
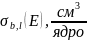 есть микроскопическое сечение
взаимодействия b-того
типа при энергии нейтрона Е с ядром
l-того
изотопа.
есть микроскопическое сечение
взаимодействия b-того
типа при энергии нейтрона Е с ядром
l-того
изотопа.
Пусть
 есть функция распределения вторичных
нейтронов, образовавшихся в некоторой
есть функция распределения вторичных
нейтронов, образовавшихся в некоторой
 -ой
ядерной реакции с l-тым
изотопом по энергии E
и направлению Ω,
если нейтрон, вызвавший реакцию имел
энергию
-ой
ядерной реакции с l-тым
изотопом по энергии E
и направлению Ω,
если нейтрон, вызвавший реакцию имел
энергию
 и направление
и направление
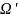 .
Нормируем вероятность:
.
Нормируем вероятность:
|
(1.3) |
Запишем уравнение Больцмана
|
(1.4) |
Производная
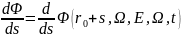 является производной по направлению
Ω.
Если dx,
dy,
dz
– проекции ds
на оси координат, то, обозначив
является производной по направлению
Ω.
Если dx,
dy,
dz
– проекции ds
на оси координат, то, обозначив
|
(1.5) |
Получаем
|
(1.6) |
Далее запишем уравнение переноса нейтронов в своем обычном виде
|
(1.7) |
Как
видно, баланс нейтронов в некоем
пространстве размножающей среды равен
суперпозиции нескольких факторов –
диффузии нейтронов,
как в данное
пространство, так и из него
 ,
убыли нейтронов за счет поглощения
,
убыли нейтронов за счет поглощения
 ,
приходу нейтронов за счет замедления
из областей большими энергиями
,
приходу нейтронов за счет замедления
из областей большими энергиями
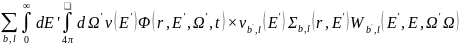 и приходу нейтронов от источника
и приходу нейтронов от источника
 .
.
Метод Монте-Карло применительно к расчету размножающих сред
Решение уравнения переноса нейтронов возможно найти как численными методами, так и методом Монте-Карло. В случаях, если геометрия и материальный состав среды достаточно сложны, численные методы применять достаточно проблематично – расчет решения займет огромное количество компьютерного времени. В таком случае удобно искать решение методом Монте-Карло. Метод Монте-Карло позволяет моделировать поведение каждой частицы в некоторой системе.
Рождается некоторая заданная частица (пусть для простоты это будет нейтрон)
Определение траектории частицы в среде, от точки рождения до некоторой точки взаимодействия. Нейтрон будет двигаться в среде прямолинейно, от одной точки взаимодействия до другой, до тех пор, пока не поглотится, либо не будет выведен из симуляции другим путем.
Моделируется взаимодействие частицы с веществом – выбор реакции, изотопа, и т. д.
Определение параметров вторичных частиц, возникающих в система, если необходимо.
Собирая информацию о каждой промоделированной частице, можно определить некоторые параметры среды. Например, коэффициент размножения для нейтронов, или потоки частиц в разных точках интересной нам системы.