1.3 Определение численных значений линейных и угловых скоростей по методу плана скоростей

Для построения плана скоростей используется теорема о распределении скоростей точек плоской фигуры:

(1.3)

где -скорость точки полюса;

-вращательная составляющая вокруг полюса А.

Рисунок 1.3- К теореме о распределении скоростей точек плоской фигуры

Причем,

Рассмотрим механизм в положениях 0-7.

Найдем величину скорости точки А

V_А= ₁ L_ОА, м/с (1.4)

где - угловая скорость кривошипа, рад /с.

V_А= м/с

Скорость точки А направлена перпендикулярно звену ОА в сторону движения механизма. Примем величину скорости т. А равной 100 мм.

(1.4)

где -отрезок, отображающий скорость точки А на чертеже.

Скорость точки В находим графически

(1.5)

(1.6)

Из конца вектора скорости точки А проводим направление , т. е. перпендикуляр к звену ВА, а из полюса проводим направление . На пересечении получим точку . Измеренный отрезок умножаем на масштаб плана скоростей и получим величину скорости точки В.

Скорость точки С находим графически

(1.7)

(1.8)

Из конца вектора скорости точки В проводим направление , т. е. перпендикуляр к звену ВС, а из полюса проводим направление . На пересечении получим точку с. Измеренный отрезок умножаем на масштаб плана скоростей и получим величину скорости точки С.

Для нахождения скорости точки Д напишем уравнение

(1.9)

Из конца скорости точки С проводим перпендикуляр к направлению звена СД. Так как точка Д движется по горизонтали, из полюса Р проводим горизонтальную линию. На пересечении найдем точку d.

Угловая скорость 2 звена

_AВ= (1.10)

Угловая скорость 3 звена

_СВ= (1.11)

Угловая скорость 4 звена

_ДС = (1.12)

Скорости центров масс найдем по формуле:

(1.13)

Полученные данные занесем в таблицу.

Таблица 1 – Значения скоростей звеньев и точек

Рисунок 1.2- План положений 0, план скоростей к положению 0

Рисунок 1.3- План положений 1, план скоростей к положению 1

Рисунок 1.4- План положений 2, план скоростей к положению 2

Рисунок 1.5- План положений 3, план скоростей к положению 3

Рисунок 1.6- План положений 4, план скоростей к положению 4

Рисунок 1.7- План положений 5, план скоростей к положению 5

Рисунок 1.8- План положений 6, план скоростей к положению 6

Рисунок 1.9- План положений 7, план скоростей к положению 7

1.4 Построение плана ускорений

Построение плана ускорений механизма основано на теореме о распределении ускорений точек плоской фигуры:

Рисунок 1.12- К теореме о распределении ускорений точек плоской фигуры

Ускорение точки В плоской фигуры

(1.14)

где - ускорение полюса;

-центростремительное ускорение;

вращательное ускорение.

(1.15)

Причем

(1.16)

Ускорение точки А кривошипа механизма определяем из уравнения

(1.17)

Так как угловая скорость первого звена постоянна, значит, = 0.

, (1.18)

Зададим, что ускорение точки A кривошипа на плане ускорений равно 100 мм. Тогда масштаб плана ускорений

, (1.19)

где - отрезок, отображающий ускорение точки А на плане ускорений

Ускорение точки В

(1.20)

(1.21)

где а_ВA^=_ВA² L_ВA= м/с²

а_ВО1^=_ВО1² L_ВО1= м/с²

Полученное значение делим на масштаб и получаем отрезок, который отложим на плане ускорений:

.

Из полюса  параллельно звену AO к центру проводим а_AO^п, из его конца параллельно звену ВA- а_ВA^, потом проводим направление а_ВA^, т. е. линию, перпендикулярную звену ВA. Из полюса  проводим а_ВО1^ параллельно ВО₁, из его конца- направление а_ВО1^, т. е. линию, перпендикулярную звену ВО₁. На пересечении получим точку .

Ускорение точки С

(1.22)

(1.23)

где а_СВ^=_СВ² L_СВ= м/с²

а_СО1^=_СО1² L_СО1= м/с²

Полученное значение делим на масштаб и получаем отрезок, который отложим на плане ускорений:

.

Из полюса  параллельно звену СO₁ проводим а_СO1^п, из его конца параллельно звену СО₁- а_СО1^. Из точки проводим а_ВС^ параллельно ВС, из его конца- направление а_ВС^, т. е. линию, перпендикулярную звену ВС. На пересечении получим точку .

Измерив полученные отрезки, умножаем на масштаб

а_C= м/с²

а_B= м/с²

а_ВA^ = м/с²

а_ВО1^ = м/с²

Ускорение точки D

(1.24)

где а_ДС^=_ДС² L_ДС= м/с²

Вычисленное значение делим на масштаб плана ускорений

откладываем из конца вектора ускорения точки С параллельно звену DС, из его конца проводим направление а_DС^, т. е. перпендикуляр к звену DС. Так как точка D движется по горизонтальной линии, из полюса проводим горизонтальную линию. На пересечении получим точку d.

а_D= м/с²

а_DС^= м/с²

Угловые ускорения звеньев:

₂=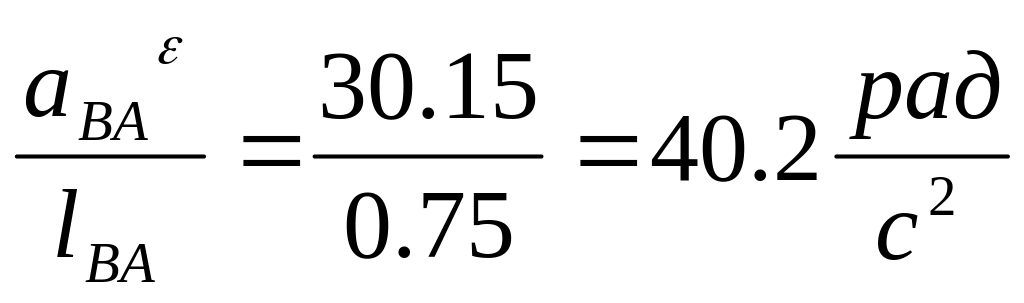

₃=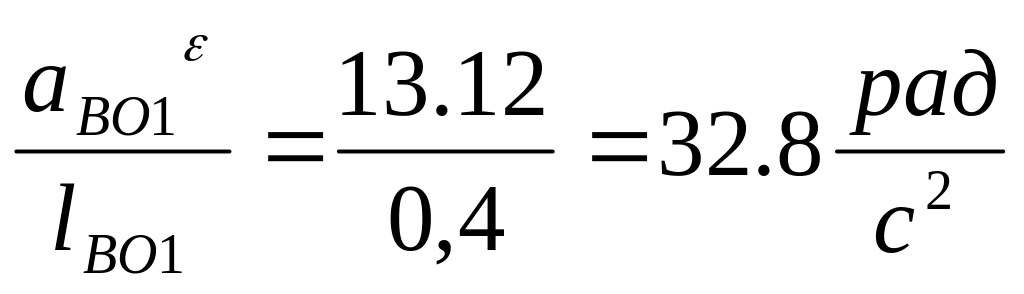

₄=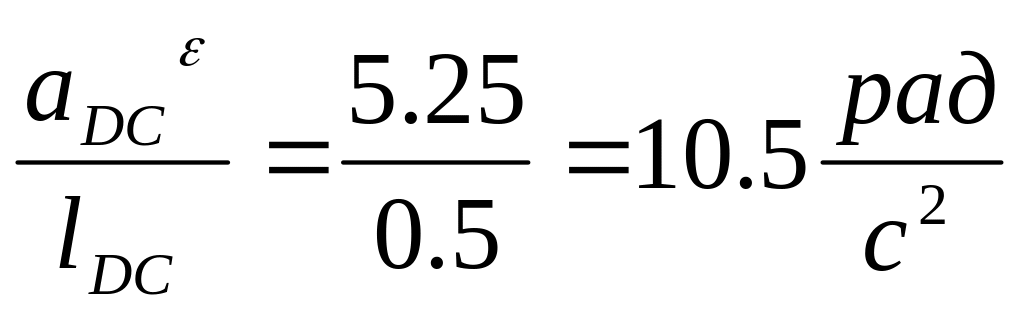

Ускорения центров масс звеньев

м/с²

м/с²

м/с²

м/с²

м/с2