Гидравлические потери на трение по длине трубопровода

Цель работы: опытное определение зависимости коэффициента потерь на трение от числа Рейнольдса и гидравлических потерь на трение от расхода.

Общие сведения о потерях на трение

При движении реальной жидкости по трубопроводу необходимо затратить энергию, которая расходуется на преодоление так называемых гидравлических сопротивлений. Они обычно разделяются на потери на трение по длине трубопровода и местные потери. Потери энергии характеризуются уменьшением полного напора по длине трубопровода. Эта «потерянная» энергия переходит в тепло.

Потери на трение по длине в чистом виде возникают при равномерном движении жидкости в прямом трубопроводе постоянного сечения. Запишем уравнение Д. Бернулли для двух сечений

.

Здесь — координата (высота) середины сечения над произвольно выбранной горизонтальной плоскостью отсчёта (для горизонтального трубопровода ); — давление, — плотность среды и — ускорение земного притяжения. Коэффициент , учитывает неравномерность распределение скоростей в - том сечении (отношение действительной кинетической энергии к кинетической энергии, определённой по средней скорости ) и — потери полного напора на трение.

Следует заметить, что ввиду постоянства расхода скорость и удельная кинетическая энергия несжимаемой среды остаются постоянными вдоль трубы постоянного сечения, несмотря на наличие любых гидравлических сопротивлений. Гидравлические сопротивления приводят к потерям напора, которые в данном случае определяются разностью показаний двух пьезометров: .

Гидравлические потери на трение возрастают пропорционально длине трубы. Их можно выразить через коэффициент по формуле Вейсбаха, но значительно удобнее их представить через коэффициент потерь на трение по длине :

.

Запись гидравлических потерь на трение во втором случае именуется формулой Вейсбаха-Дарси.

К

Рис. 2.1. Зависимость кинематического коэффициента вязкости воды от температуры.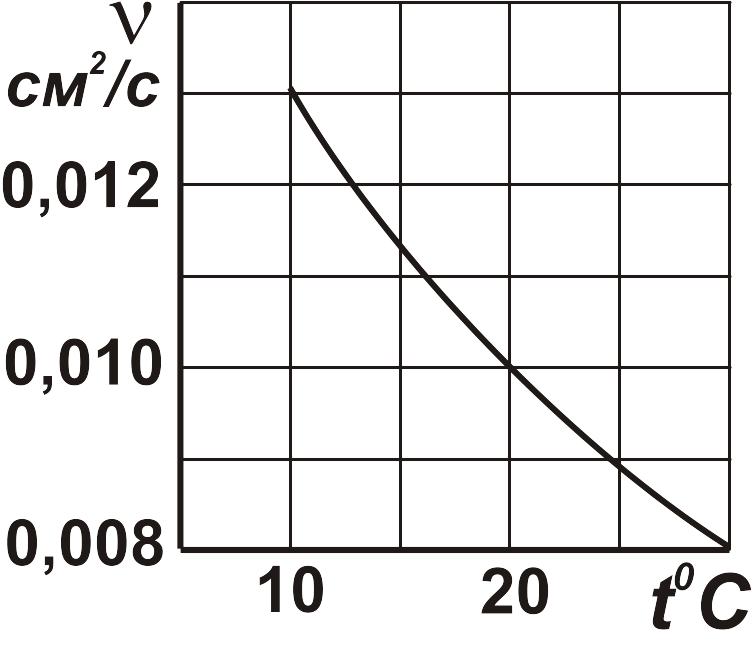

оэффициент потерь на трение в общем случае зависит от значения основного параметра подобия для вязких течений — числа Рейнольдса ( ), характера течения (ламинарное или турбулентное) и от состояния внутренней поверхности трубопровода. Здесь — кинематический коэффициент вязкости; его значения для воды приведены на рис 2.1.

Считается, что переход ламинарной формы течения в турбулентную и обратно происходит при критическом числе . Для круглого трубопровода это значение равно приблизительно . Однако эта величина зависит также от направления изменения числа и от наличия возмущений.

При ламинарном течении ( ) силы вязкости имеют преобладающее значение, элементы шероховатости стенок обтекаются плавно, практически не возмущая основное течение. Поэтому при ламинарном течении шероховатость практически не оказывает влияния на коэффициент трения. При ламинарном течении потери на трение линейно зависят от расхода.

При увеличении числа течение становится турбулентным, и в нём возникают мощные пульсации. Однако стенки трубопровода стабилизируют течение, и вблизи них образуется так называемый ламинарный подслой. Пока элементы шероховатости находятся внутри этого подслоя, они не оказывают влияние на величину потерь на трение. Труба в этом случае называется гидравлически гладкой. Однако с увеличением числа толщина ламинарного подслоя уменьшается, и элементы шероховатости выступают за его границы. Это приводит к увеличению сопротивления на трение. С этого значения числа труба считается гидравлически шероховатой. При очень больших значениях числа коэффициент потерь на трение зависит только от шероховатости, и потери на трение зависят уже от . Следует заметить, что при фиксированном расходе потери на трение очень сильно зависят от диаметра трубопровода: при ламинарном течении они обратно пропорциональны , а при очень больших числах — уже .