Моделирование потенциального обтекания плоского тела

Следует отметить, что при решении различных задач обычно используется два вида установок: ЭГДА-А и ЭГДА-Б. Рассмотрим электрическое моделирование этой задачи на установке ЭГДА-А (рис. 7.2). При моделировании необходимо соблюсти геометрическое подобие обтекаемого тела и границ потока. Это достигается соответствием граничных условий при обтекании тела ( и ) аналогичным условиям электрической модели ( и ).

При моделировании на установке ЭГДА-А линии равного потенциала электрического поля соответствуют эквипотенциальным линиям среды , а силовые линии электрического поля — линиям тока в несжимаемой среде .

Э

квипотенциальные линии и силовые линии электрического тока образуют ортогональную сетку. Для построения линий тока течения в электрической модели необходимо поменять местами эквипотенциальные и силовые линии, а модель выполнить из очень хорошего проводника (рис. 7.2). Установка, на которой выполняется это взаимное обращение условий, получила наименование ЭГДА-Б.

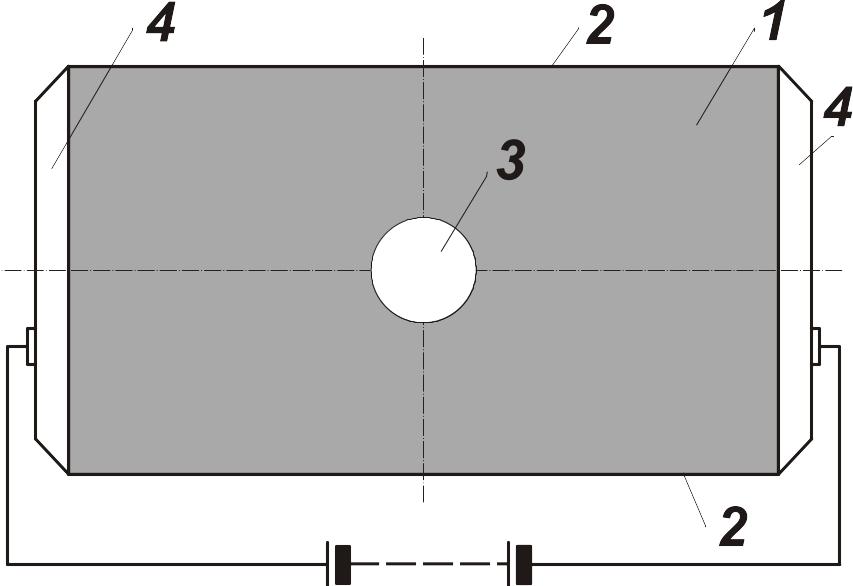
а) ЭГДА-А б) ЭГДА-Б Рис. 7.2. Моделирование обтекания тела бесциркуляционным потенциальным потоком на установке ЭГДА. Здесь: 1 — электропроводная бумага, 2 — изолированные границы, 3 — исследуемое тело (А —- отверстие, Б — металл) и 4 — шины-зажимы.

Таким образом, граничное условие заменяется эквивалентным условием . Аналогично вместо условия используют . Измерив электрический потенциал в различных точках на листе электропроводной бумаги и соединив линиями точки с одинаковыми значениями потенциала, получаем линии равного электрического потенциала. В этом случае они будут соответствовать линиям тока в потоке несжимаемой среды.

В результате моделирования с помощью аналогий и можно построить ортогональную сетку линий тока и эквипотенциальных линий, что позволяет выполнить расчет потенциального обтекания тела.

Подготовка, проведение эксперимента и обработка его результатов

1. Построение линий тока при данном моделировании выполняется на установке ЭГДА-Б. Удобно его начинать с построения т. н. нулевой линии тока, которая включает в себя контур исследуемого тела. Для этого одинарной иглой измеряют и записывают значения электрического потенциала на модели. Затем проводят эту линию тока (её потенциал равен потенциалу тела), перемещая иглу от модели сначала в одну, а затем и в другую стороны. Точки, зафиксированные измерительной иглой, необходимо соединить плавной линией. Эти точки и соединяющие их линии на чёрной электропроводной бумаге удобно наносить цветным карандашом. Затем аналогично строят ещё 2-3 линии тока, уже обтекающие исследуемое тело. Эти линии можно строить для заданных значений напряжения.

2. Аккуратно вырезав металлическую модель, получим в листе электропроводной бумаги отверстие в форме модели. Присоединив к листу шины-зажимы, получим установку ЭГДА-А.

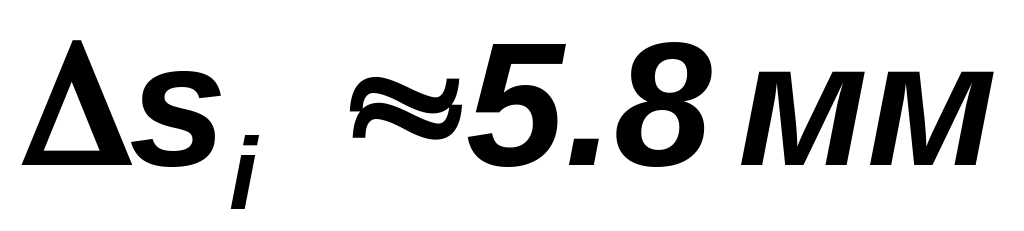3. Задав длину (обычно принимают ), снимаем показания вдали от обтекаемого тела. Для повышения точности их желательно снимать в четырёх углах листа. Если дальнейшие измерения на поверхности тела будут проводится с постоянным шагом , то после осреднения результатов необходимо получить величину и вычислить коэффициент . Если контур круга разделён равномерно на 36 частей (через ), то ( и — расстояния между точками, в которых определяется напряжение).