
- •2.2. Коды и геометрическое представление конъюнкций
- •2.3. Табличный метод построения множества минималей Квайна - Мак-Класки
- •2.4. Построение минимальных покрытий для функций, имеющих экстремали
- •2.5. Неизбыточные покрытия, алгоритм извлечения экстремалей
- •2.6. Построение минимальных покрытий для функций, не имеющих экстремалей
2.2. Коды и геометрическое представление конъюнкций
Элементарные
конъюнкции отличаются расстановкой
знаков отрицания над переменными,
поэтому каждая такая конъюнкция
однозначно определяется двоичным
набором
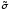 ,
на котором она принимает значение
единицы. Задание конъюнкций рангаrn
с
помощью двоичных наборов не является
однозначным, поскольку по такому набору
нельзя установить, какие переменные
входят в конъюнкцию. Для указания
отсутствующих переменных вводят третье
значение компонентов определяющего
набора, которое обозначают буквой z.
При этом считают, что эта буква, стоящая
на i-м
месте в наборе, определяющем конъюнкцию,
показывает, что переменная хi
в рассматриваемой конъюнкции отсутствует.
Тогда набор 0zz10
определяет конъюнкцию
,
на котором она принимает значение
единицы. Задание конъюнкций рангаrn
с
помощью двоичных наборов не является
однозначным, поскольку по такому набору
нельзя установить, какие переменные
входят в конъюнкцию. Для указания
отсутствующих переменных вводят третье
значение компонентов определяющего
набора, которое обозначают буквой z.
При этом считают, что эта буква, стоящая
на i-м
месте в наборе, определяющем конъюнкцию,
показывает, что переменная хi
в рассматриваемой конъюнкции отсутствует.
Тогда набор 0zz10
определяет конъюнкцию
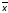 1
1 4
4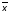 5,
набор z1011
- конъюнкцию
5,
набор z1011
- конъюнкцию
 2
2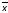 3
3 4
4 5,
а набор zz0zz
- конъюнкцию
5,
а набор zz0zz
- конъюнкцию
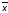 3.
Компоненты набора, равные 0 и 1, называют
связанными
компонентами,
а компоненты, равные z
- свободными
компонентами.
Число связанных компонентов набора
называют рангом этого набора. Ранг
набора всегда совпадает с рангом
конъюнкции, соответствующей этому
набору.
3.
Компоненты набора, равные 0 и 1, называют
связанными
компонентами,
а компоненты, равные z
- свободными
компонентами.
Число связанных компонентов набора
называют рангом этого набора. Ранг
набора всегда совпадает с рангом
конъюнкции, соответствующей этому
набору.
В параграфе 2.1 описан способ задания переключательных функций в виде совокупностей конъюнкций, соответствующих некоторой ДНФ функции. Подобно этому способу, можно использовать задание функций в виде совокупности определяющих наборов (кодов), поскольку между конъюнкциями и наборами установлено взаимно однозначное соответствие. Обозначим множество наборов ранга r, связанных с заданной функцией, Cr(), а комплекс всех наборов - C(), причем C() = C n() C n-1() ... C1().
Используя соответствие между конъюнкциями и кодами, нетрудно сформулировать правила выполнения операций склеивания и расширения применительно к троичным кодам. Два набора одного и того же ранга, у которых свободные компоненты расположены на одинаковых местах, а все связанные компоненты, за исключением одного, совпадают, называются смежными. Смежные коды соответствуют склеивающимся конъюнкциям.
Между
конъюнкциями и кодами существует взаимно
однозначное соответствие. Например,
кодам 001 и 011, которые являются смежными,
соответствуют конъюнкции 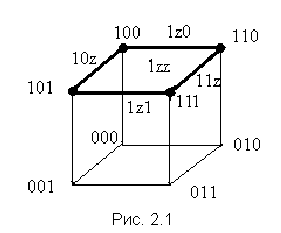
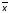 1
1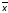 2
2 3
и
3
и
 1
1 2
2 3,
при склеивании которых получаем
конъюнкцию меньшего ранга:
3,
при склеивании которых получаем
конъюнкцию меньшего ранга:
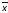 1
1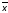 2
2 3
3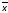 1
1 2
2 3
=
3
=
 1
1 3(
3( 2
2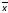 2)
=
2)
=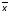 1
1 3,
которой соответствует код 0z1.
3,
которой соответствует код 0z1.
В
случае геометрического представления
склеивающимся наборам
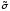 Cn()
соответствуют вершины куба, соединенные
ребром, как это показано на рис. 2.1.
Обозначим каждое ребро верхней грани
куба кодом конъюнкции ранга n-1,
представляющим собой результат склеивания
противоположных вершин. Тогда
противолежащие ребра, находящиеся в
одной плоскости, будут соответствовать
склеивающимся конъюнкциям ранга n-1.
При этом грань куба можно обозначить
кодом 1zz,
полученным в результате склеивания
кодов, соответствующих противоположным
ребрам.
Cn()
соответствуют вершины куба, соединенные
ребром, как это показано на рис. 2.1.
Обозначим каждое ребро верхней грани
куба кодом конъюнкции ранга n-1,
представляющим собой результат склеивания
противоположных вершин. Тогда
противолежащие ребра, находящиеся в
одной плоскости, будут соответствовать
склеивающимся конъюнкциям ранга n-1.
При этом грань куба можно обозначить
кодом 1zz,
полученным в результате склеивания
кодов, соответствующих противоположным
ребрам.
Соответствие между гранями куба и кодами показано на рис. 2.2. Для наглядности на рис. 2.2а жирными линиями показаны видимые, а на рис. 2.2б – невидимые грани 3-х мерного куба.
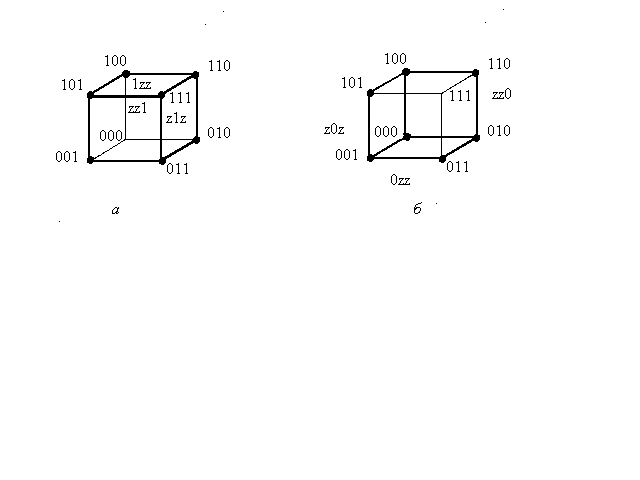 Рис.2.2
Рис.2.2
В общем случае соответствие между конъюнкциями, кодами и гранями гиперкубов сохраняется для любых рангов.
Результат склеивания смежных кодов можно получить путем замены в любом из них связанного компонента, которым они отличаются, свободным компонентом z. Например, наборы 01zz1z и 01zz0z являются смежными. В результате их склеивания получается набор 01zzzz. Исходным кодам соответствуют трехмерные грани шестимерного гиперкуба, а результату склеивания соответствует четырехмерный гиперкуб, являющийся частью шестимерного гиперкуба.
Совокупность
двоичных наборов, из которых с помощью
операции склеивания может быть получен
код “а”,
назовем интервалом
этого кода и будем обозначать С(а).
Построение интервала С(а)
по заданному коду “а”
может быть выполнено с помощью операции
расширения. Эта операция заключается
в том, что каждый свободный компонент
а
последовательно заменяется 0 и 1. Если
код а
= (а1,
а2,
..., аn)
имеет
 свободных
компонентов, то в результате операции
расширения получается 2
свободных
компонентов, то в результате операции
расширения получается 2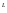 двоичных наборов ранга n.
Например, интервал кода а
=
01zz1
имеет вид: С(а)
= {01001, 01011, 01101, 01111}.
двоичных наборов ранга n.
Например, интервал кода а
=
01zz1
имеет вид: С(а)
= {01001, 01011, 01101, 01111}.
