6. Преобразование в универсальный функциональный базис

По результатам совместной минимизации выбираем для реализации минимальную совместную систему ДНФ с суммарной сложностью 31 единиц, поскольку минимальная совместная система КНФ имеет сложность 39 единиц, а следовательно, будем использовать универсальный базис Шеффера.

Общая таблица минимальных покрытий ДНФ:

Импликанты	Ранг	Y1	Y2	Y3	Y4
00zz	2	1	-	1	-
zz01	2	1	-	-	-
z11z	2	1	-	-	-
0z01	3	-	1	-	-
1z11	3	-	1	-	-
11zz	2	-	-	1	-
zz10	2	-	-	1	-
z0z0	2	-	-	-	1
z111	3	-	-	-	1

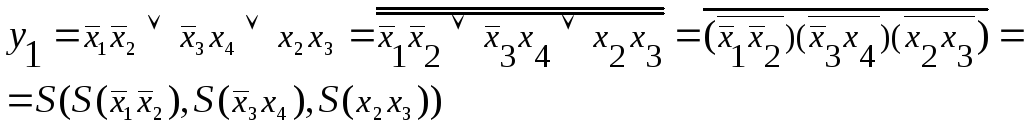
После выделения общих частей получаем совместную систему уравнений в операторной форме:

7. Построение комбинационной схемы

Схема строится на основании совместной системы уравнений в операторной форме, полученной в предыдущем параграфе. При этом каждому оператору универсального базиса Шеффера в системе уравнений соответствует логический элемент «И-НЕ» (элемент Шеффера). Число входов элемента соответствует местности оператора.

C1

Y1

Y2

Y3

Y4

&

&

&

&

&

&

&

&

&

&

&

8. Учет местности операторов универсального

функционального базиса

По результатам предыдущего этапа преподаватель задал местность операторов универсального функционального базиса, равную трем ( t = 2). Выполним эквивалентные преобразования уравнений из параграфа 6, используя только трехместные операторы Шеффера.

9. Учет ограничения на число входов

универсального структурного базиса

Данный параграф содержать комбинационную схему с разветвлениями из элементов выбранного универсального структурного базиса («И-НЕ» («элемент Шеффера») c учетом ограничений на число входов элементов t. Схема строится на основе операторного представления минимальной совместной системы переключательных функций из параграфа 8.

ПРИМИЧАНИЕ: (схема представлена на следующей странице)

C1

&

Y1

Y2

Y3

Y4

&

&

&

&

1

&

&

&

&

1

&

1

&

&

&

&

&

1

&

&

&

&

&

1

&

&