Анализ переходных процессов методом наложения.

При использовании метода наложения для анализа переходных процессов необходимо знать так называемые временные характеристики цепи: переходную характеристику или импульсную реакцию .

Переходной характеристикой электрической цепи называется отклик этой цепи на единичную функцию .

Импульсной реакцией электрической цепи называется отклик этой цепи на единичный импульс .

Между этими двумя характеристиками имеется следующая связь:

Переходную характеристику легко найти, если известна соответствующая (в зависимости от вида отклика и воздействия) комплексная частотная характеристика:

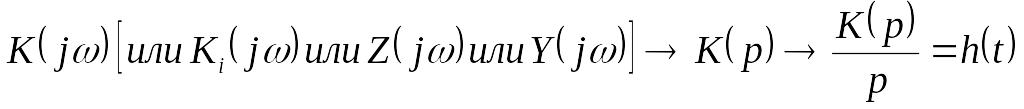
Зная переходную характеристику цепи и воздействие , можно найти отклик цепи , используя одну из формул интеграла Дюамеля:

1.

2.

3.

4.

Если импульсная реакция цепи , то отклик может быть найден следующим образом:

или

Численные методы анализа переходных процессов в электрических цепях.

Рассмотренные выше методы анализа переходных процессов есть не что иное, как различные методы решения систем дифференциальных уравнений. Причем эти методы обычно применяются для анализа переходных процессов в относительно несложных цепях (степень характеристического уравнения чаще всего не выше четырех).

В связи с необходимостью анализа переходных цепей, содержащих большое число реактивных элементов, и, особенно, нелинейных цепей в настоящее время получили распространение методы, основанные на численном решении дифференциальных уравнений с помощью ЭВМ.

Одним из наиболее распространенных численных методов решения систем дифференциальных уравнений в настоящее время является метод Рунге – Кутта. С его применением можно познакомиться в [4].

Пример выполнения домашнего задания по тоэ №3.

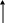
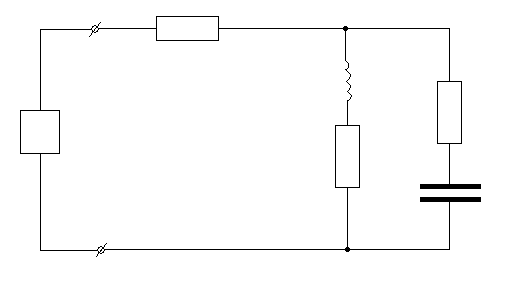
Пусть дана цепь

( рис. 1) со следующими параметрами:

10мГн, С=1мкФ

Рис. 1

1). Для выяснений условий колебательного процесса составим характеристическое уравнение. С этой целью запишем выражение для комплексной проводимости между узлами «с» и «b», отключив от схемы генератор тока:

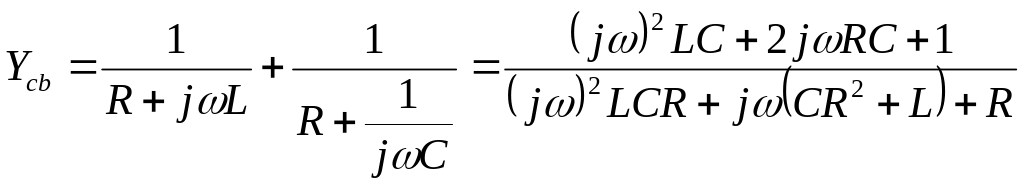
Далее в полученное выражение подставим вместо и приравняем его к нулю:

Следовательно, характеристическое уравнение имеет вид:

Необходимым условием колебательного переходного процесса является наличие среди корней характеристического уравнения хотя бы одной пары комплексно – сопряженных корней.

Характеристическое уравнение, очевидно, имеет комплексно сопряженные корни, если дискриминант его меньше нуля:

Или

Отсюда условие колебательного переходного процесса имеет вид:

Пусть R=10 Ом.

2). Найдем переходную характеристику цепи (рис. 4), считая откликом напряжение . Для этого найдем сопротивление между точками «с» и «b» в операторной форме:

Подставляя значения L=10мГн, С=1,0мкФ, R=10 Ом, получим:

Таким образом:

или

По определению переходной характеристики при и, т.к. имеем

По теореме разложения определим оригинал от :

По знаменателю находим корни:

; ;

Поделив на , получим:

.

Переходя к оригиналу в правой части, получим:

График переходной характеристики показан на рис. 2.

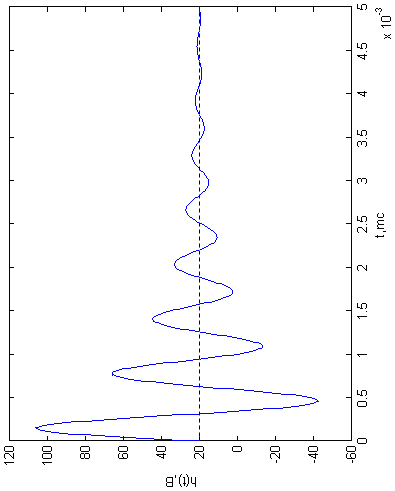
В заключении выполнения задания требуется построить график изменения данного отклика на заданное сложное ступенчатое воздействие.

Пусть для рассматриваемого примера требуется найти закон изменения для воздействия, показанного на

рис. 3.

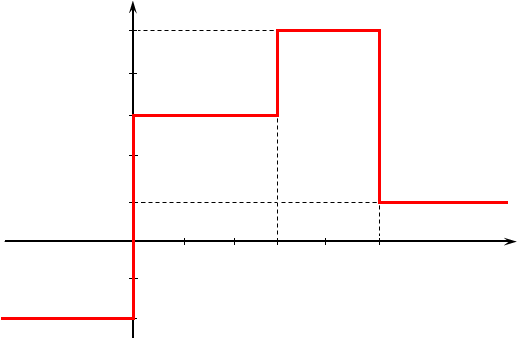
Рис. 3.

Данное воздействие можно представить в виде суммы следующих слагаемых:

Отклик на постоянное воздействие найти легко:

Тот же отклик на заданное воздействие с определением переходной характеристики, очевидно имеет вид:

График этого отклика показан на рис. 4.

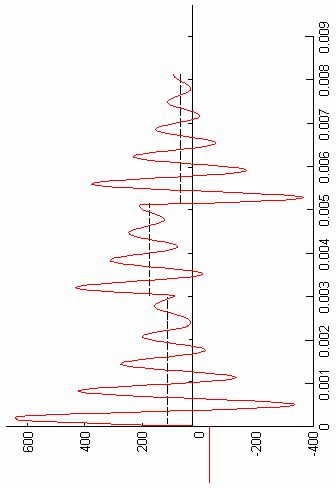
Список литературы

1. Атабеков Т.И. Теоретические основы электротехники. - М.: Энергия, 1970.

2. Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. - М.: Высшая школа, 1978.

3. Шебес М.Д. Теория линейных электрических цепей в упражнениях и задачах. - М.: Высшая школа, 1967.

4. Шаров В.К., Широков Г.И., Червяков В.И. Алгоритмическое и программное обеспечение для расчета электрических цепей с помощью ПЭВМ. – учебное пособие по выполнению домашних заданий и курсовой работы по курсу ТОЭ. Калуга 1997.

22