
- •Задания по теме «Линейное программирование»
- •Найти область решений и область допустимых решений системы неравенств
- •Составить математическую модель и решить задачу графическим методом.
- •Составить математическую модель симметричной двойственной задачи. По решению двойственной или исходной задачи найти решение другой с использованием основных теорем двойственности.
- •Решить задачу о назначении с использованием симплексного метода.
- •Задания по теме «Нелинейное программирование»
- •Задания по теме «Динамическое программирование»
- •Задания по теме «Сетевые модели»
- •5. Задания по теме «Теория игр»
- •5.1. Найти оптимальные стратегии и цену игры, заданной платежной матрицей.
- •5.2. Решить задачу с использованием «дерева» решений.
- •6. Задания по теме «Система массового обслуживания»
- •1. Задания по теме «Линейное программирование»
- •1.1. Найти область решений и область допустимых решений и определить координаты угловых точек области допустимых решений системы неравенств:
- •Решить задачу симплексным методом при стремлении целевой функции к максимальному и минимальному значениям.
- •Решить транспортную задачу, заданную распределительной таблицей:
- •Решить задачу о назначениях.
- •2. Задания по теме «Нелинейное программирование»
- •3. Задания по теме «Динамическое программирование»
- •4. Задания по теме «Динамическое программирование»
- •5. Задания по теме «Теория игр»
- •5.2. Решить задачу с использованием «дерева» решений.
- •6. Задания по теме «Система массового обслуживания»
- •1. Задания по теме «Линейное программирование»
- •1.1. Дана задача линейного программирования. Графическим методом найти оптимальные решения.
- •1.2. Составить математическую модель и решить задачу симплексным методом.
- •1.3. Решить транспортную задачу, заданную распределительной таблицей:
- •1.4. Решить задачу о назначениях.
- •2. Задания по теме «Нелинейное программирование»
- •3. Задания по теме «Динамическое программирование»
- •4. Задания по теме «Динамическое программирование»
- •5. Задания по теме «Теория игр»
- •5.2. Решить задачу с использованием «дерева» решений.
- •6. Задания по теме «Система массового обслуживания»
ВАРИАНТ А
Задания по теме «Линейное программирование»
Найти область решений и область допустимых решений системы неравенств

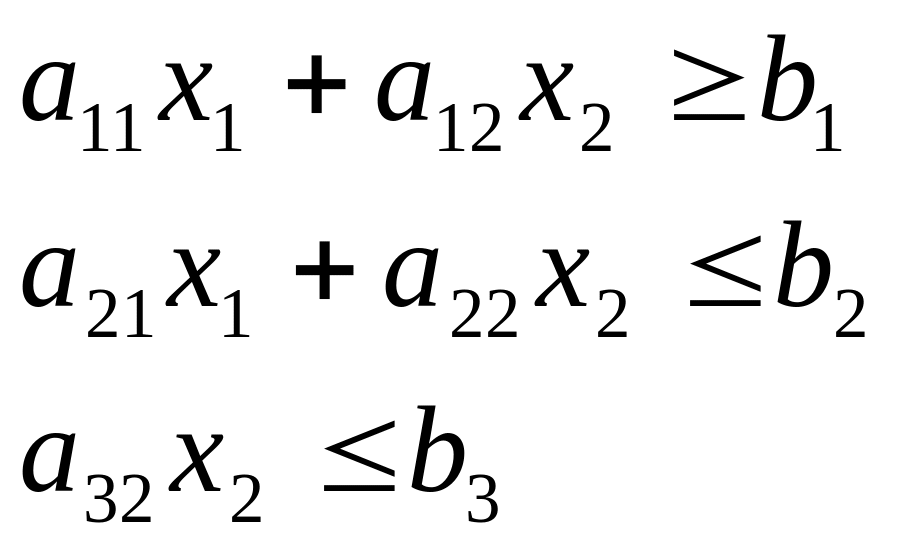
Значения коэффициентов системы ограничений системы неравенств:
№ варианта значения |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
a11 |
-5 |
6 |
-3 |
5 |
5 |
1 |
1 |
5 |
10 |
1 |
a12 |
7 |
-4 |
2 |
-7 |
4 |
1 |
1 |
4 |
-5 |
1 |
b1 |
35 |
24 |
6 |
35 |
20 |
1 |
7 |
20 |
50 |
2 |
a21 |
5 |
7 |
1 |
9 |
7 |
-1 |
4 |
-3 |
6 |
-1 |
a22 |
6 |
4 |
1 |
7 |
2 |
1 |
-3 |
5 |
5 |
1 |
b2 |
30 |
28 |
3 |
63 |
14 |
4 |
12 |
15 |
30 |
2 |
b3 |
6 |
3 |
-4 |
-4 |
4 |
-1 |
-3 |
6 |
-2 |
5 |
a32 |
1 |
1 |
-1 |
-1 |
1 |
-1 |
-1 |
1 |
-1 |
1 |
Составить математическую модель и решить задачу графическим методом.
Фирма изготавливает два вида красок для внутренних (В) и наружных (Н) работ. Для их производства используют исходные продукты: пигмент и олифу. Расходы исходных продуктов и максимальные суточные запасы указаны в таблице.
Исходный продукт |
Расход исходных продуктов на 1 т краски |
Суточный запас, т |
|
Краска Н |
Краска В |
||
Пигмент |
a11 |
a12 |
b1 |
Олифа |
a21 |
a22 |
b2 |
Изучение рынка сбыта показало, что суточный спрос на краску для наружных (внутренних) работ никогда не превышает b3 в сутки. Цена продажи 1 т краски для наружных работ – c1 ден.ед., для внутренних работ - c2 ден.ед.
Какое количество краски каждого вида должна производить фирма, чтобы доход от реализации продукции был максимальным?
Значения коэффициентов условий задачи:
№ варианта значения |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
c1 |
3 |
1 |
1 |
2 |
3 |
2 |
1 |
3 |
2 |
4 |
c2 |
2 |
1 |
4 |
2 |
2 |
1 |
2 |
4 |
3 |
5 |
a11 |
1 |
2 |
3 |
3 |
1 |
3 |
3 |
1 |
1 |
1 |
a12 |
2 |
1 |
2 |
1 |
1 |
4 |
1 |
1 |
1 |
2 |
b1 |
6 |
6 |
12 |
3 |
4 |
24 |
6 |
6 |
7 |
8 |
a21 |
2 |
1 |
1 |
3 |
4 |
2 |
1 |
2 |
2 |
4 |
a22 |
1 |
2 |
2 |
2 |
1 |
1 |
1 |
1 |
1 |
3 |
b2 |
8 |
6 |
6 |
12 |
8 |
8 |
5 |
8 |
10 |
24 |
k1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
k2 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
b3 |
2 |
2.5 |
3.5 |
4 |
4 |
3 |
1 |
4.5 |
6 |
3 |
Примечание. Если по условию задания спрос на краску для наружных (внутренних) работ не превышает b3 т в сутки, то в математической модели задачи следует принять, что коэффициент системы ограничений при неизвестном значении краски для наружных (внутренних) работ, обозначенный в таблице k1 (k2), равен 1 (0), а при неизвестном значении для внутренних (наружных) работ k2 (k1) равен 0 (1).
