Вступ

Еволюція сучасної науки характеризується глибоким проникненням математичних методів дослідження у різні сфери наукової думки – від суто гуманітарних дисциплін до таких, як соціологія, прикладна лінгвістика, екологія, що розвиваються на зламі кількох наукових напрямів. Це певною мірою стосується різних галузей природознавства, де роль математики істотно зростає.

Обробка експериментальних даних з використанням математичної статистики – це лише найпоширеніше, але не найважливіше застосування математики. Справа в тому, що результати навіть досить тонких експериментів далеко не завжди дозволяють відповісти на запитання, які основні рушійні сили і механізми впливають на стан і розвиток тієї чи іншої природної системи. Такі механізми можуть бути визначені при розгляді функціонування біологічної чи екологічної системи як результату взаємодії її складових елементів і зовнішніх факторів, що позначаються на стані середовища, в якому розглядаються ці системи. Дослідити згадану взаємодію різноманітних чинників можна тільки за допомогою математичних методів і методів математичного та імітаційного моделювання

Найважливішим етапом застосування математики в екології слід вважати процес побудови адекватної математичної моделі об’єкта або системи, що вивчається.

Зокрема нижче розглянемо просторову модель, яка будується на основі диференціальних рівнянь у частинних похідних, що описує процес переносу забруднень у нерухомому повітряному або водному середовищі. І реалізуємо розв’язування рівняння, що відповідає цій моделі за допомогою чисельного методу сіток.

1.Постановка задачі

2.Одновимірні моделі розповсюдження речовини в нерухомому середовищі

У випадку одномірного процесу переносу (розповсюдження) забруднень у нерухомому повітряному або водному середовищі математичну модель одержуємо у такому вигляді:

, (2.1)

де D – коефіцієнт молекулярної дифузії (м /сек); - концентрація речовини, що забруднює повітряне (водне) середовище, або густина організмів, що розповсюджуються в навколишньому середовищі (кг/м , г/дм і т. ін.); 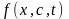- функція, що описує інтенсивність (швидкість) джерела забруднень, витікання речовини з даної екосистеми або швидкість фізичного, хімічного і біологічного перетворення речовини (наприклад, процеси седиментації, хімічного і біологічного самоочищення водойм); - просторова і часова координати.

Розглянемо спочатку найбільш прості моделі, що описуються окремими випадками рівняння (2.1).

2.1.Стаціонарна модель молекулярної дифузії без джерел і перетворень

Якщо забруднення (або мікроорганізми) розповсюджуються в нерухомому середовищі (відсутність вітру або течії у водоймищі), то стаціонарна модель цього процесу за відсутності в системі джерел і самоочищення описується таким рівнянням:

. (2.2)

Даний процес розглядатимемо на кінцевому проміжку розповсюдження забруднень від точки до точки . Для наочності розглянемо розповсюдження стічних вод, що потрапляють в озеро видовженої форми, тобто довжина озера значно більша за його ширину. Процес розповсюдження забруднень визначається не тільки рівнянням, що його описує, а й додатковими умовами, що виконуються на границях проміжку. У даному разі ці умови повинні виконуватись в точках і .

Після інтегрування рівняння (1.2) два рази знайдемо його загальний розв'язок:

, (2.3)

де і - поки що невідомі параметри.

Для визначення параметрів і скористаємося додатковими умовами, які можуть бути у трьох різних варіантах додаткових умов.

1. Відомі значення концентрацій забруднення на границях ділянки (озера), де розповсюджується забруднення, а саме:

, , (2.4)

де – концентрація забруднених стоків, що скидаються в озеро в точці , - концентрація забруднених стоків у точці на відстані від точки .

Використовуючи (2.3) і додаткові умови (2.4), одержимо:

(2.5)

Розв’язавши систему лінійних рівнянь (2.5), знайдемо невідомі параметри:

, . (2.6)

Отже, підставивши в праву частину рівності (1.3) знайдені значення і , одержимо шуканий розв’язок (математичну модель) у такому вигляді:

. (2.7)

Для спрощення одержаної формули (2.7) доцільно покласти і . Тоді одержимо:

. (2.8)

Якщо концентрацію забруднень у стічних водах позначимо через , а концентрацію забруднень у воді в кінці озера – через , то формула (2.8) матиме такий вигляд:

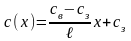. (2.9)

Формула (2.9) є шуканою математичною моделлю стаціонарного процесу розповсюдження забруднень у кінцевій, так званій функціональній формі (у даному випадку у вигляді лінійної функції).

2. На межі , тобто в точці скидання стічних вод, відомі концентрація і градієнт забруднень, тобто:

, . (2.10)

Скориставшись загальним розв’язком (1.3) і додатковими умовами (1.10), шукану математичну модель запишемо в такому вигляді:

. (2.11)

3. Якщо градієнт забруднень заданий у кінцевій точці , то математична модель матиме вигляд (2.10), тобто цей випадок збігається з попереднім. Це цілком зрозуміло, оскільки у випадку лінійного розв'язку градієнт концентрації забруднень вздовж усієї ділянки їх розповсюдження не змінюється .

Використовуючи розв’язок (2.11), можна знайти таку точку на ділянці розповсюдження забруднень, в якій вода буде чистою , а саме:

, . (2.12)

Отже, якщо в процесі розповсюдження забруднень діє тільки механізм молекулярної дифузії, то таке розповсюдження забруднень відбувається за лінійним законом, який виражається у вигляді рівності (2.9) або (2.11).