Квазивиды. Катастрофа мутационных ошибок

• Д инамику комплекса самовоспроизводящихся молекул можно описать следующей системой дифференциальных уравнений (Эйген, Шустер, 1982)

• где i — индекс различных типов самовоспроизводящихся молекул, характеризующий закодированную в них информацию. Символ X_i обозначает i-ю популяционную переменную или ее концентрацию. Данная система уравнений включает в себя те самовоспроизводящиеся единицы, которые присутствуют в рассматриваемой системе и которые могут быть пронумерованы от 1 до N. Если в ходе эволюции появляются различные мутанты, то система может быть расширена.

• Эти уравнения описывают открытую систему. В данной формализации метаболизм представлен спонтанным синтезом (A_iQ_ix_i) и дезинтеграцией (D_ix_i) молекулярного вида. «Спонтанность» в данном контексте означает, что обе реакции не являются взаимно обратимыми. Член A_i содержит какую-либо стехиометрическую функцию f_i(m₁, m₂.....m_λ) концентраций высокоэнергетического строительного материала, необходимого для синтеза молекулярного вида i. Точная форма функции зависит от конкретных механизмов реакций. Этот высокоэнергетический строительный материал постоянно поступает с притоком вещества, а продукты реакций элиминируются соответствующим оттоком (Ф_i). Член D_i, описывает спонтанное разложение. Он линейно связан с x_i по обычному закону первого порядка. Однако, в более сложных системах как синтез, так и деградация могут катализироваться ферментами, реакции могут иметь дополнительные связи, и тогда как A_i, так и D_i могут включать в себя другие функции концентраций.

• Самовоспроизведение — описывает образование x_i как функцию от x_i. Простейшая форма автокатализа описывается прямой линейной зависимостью. Аналогичным образом можно рассматривать более сложные линейные механизмы, например комплементарное инструктирование (синтез матрицы по матрице) или циклический катализ.

• Мутабильность описывается через фактор качества Q_i, который может принимать любое значение между нулем и единицей. Значение Q_i определяет ту долю репродуктивных копий, которые образуются на данной матрице с образованием ее точной копии. Дополнительный член — A_i (1 - Q_ix_i), относится к неточной репродукции матрицы i. Он описывает образование разнообразных «ошибочных копий». В большинстве случаев эти копии очень мало отличаются от вида i.

• Появление этих ошибочных копий вида i учитывается соответствующими членами в динамических уравнениях для его «родственников» k. А копия i получает вклады от этих «родственных видов» из-за ошибок в их репликации. Они учитываются суммой . Значение параметра w_ki, задающего индивидуальный темп мутаций, тем меньше, чем больше различие между i и k. Обычно w_ki мал по сравнению со скоростью репродукции A_iQ_i .

• Е сли присутствуют все виды и все их возможные мутанты учитываются индексами i и k ( i=1,N; k=1,N), то для ошибочных копий выполняется следующий закон сохранения:

• Д 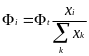обавление или удаление вида i любым способом, кроме химической реакции описывается членом Ф_i. Этот член задает индивидуальный поток или транспорт. С его помощью учитываются метаболические превращения. Суммарный поток Ф_t подсчитывается как нормированная сумма вкладов всех видов, поскольку в большинстве случаев каждый вид вносит вклад в суммарный поток в соответствии со своим изобилием:

• С 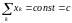уммарный поток в эволюционных экспериментах можно подобрать так, чтобы обеспечивалось поддержание воспроизводимых глобальных условий — например, таких, как постоянство суммарной плотности популяции:

• Д 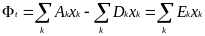ля поддержания постоянной суммарной плотности популяции поток Ф_t необходимо постоянно изменять так, чтобы компенсировать избыточную общую продукцию, т. е.

Величина E_i = A_i - D_i является «избыточной продуктивностью» матрицы i. Благодаря уравнению сохранения , ошибки не влияют на вид этой суммы.

• М 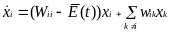ожно ввести дополнительное ограничение - ограничение «постоянной общей организации»,- при котором как суммарное количество организованного материала, так и количество неорганизованного материала поддерживаются на постоянном уровне благодаря регуляции потоков. Обычно такое ограничение выполняется в эволюционных экспериментах, например в проточном реакторе. Тогда при условии соблюдения ограничения постоянной общей организации кинетические уравнения в сочетании с дополнительными условиями — принимают следующий вид:

где величину

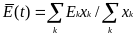Wii = AiQi - Di

можно назвать внутренней селективной ценностью, а величину

— средней избыточной продуктивностью, которая является функцией времени. В момент, когда популяционные переменные x_k(t) становятся постоянными (dx_k(t)/dt=0), E(t) принимает стационарное значение, которое является метастабильным, т.к. зависит от полноты спектра мутантов, т.е. от того сколько мутантов присутствуют из всех возможных в системе. Для постоянных (т. е. не зависящих от времени) значений W_ii и w_ik нелинейная система дифференциальных уравнений может быть решена.

КОНЦЕПЦИЯ КВАЗИВИДА

• В рассматриваемых формулировках, виды связаны друг с другом благодаря процессу мутирования, т.е. отдельный вид не является независимой единицей. Условие постоянства общей организации, а точнее - сохранение суммарной численности популяций всех матриц вынуждает все виды матриц («оригинальных» и мутантов) конкурировать друг с другом. Однако мутабильность допускает совместное существование (в некотором смысле кооперацию), особенно между близкородственными видами (т. е. видами i и k, для которых w_ik≠0 и w_ki≠0).

• Р еорганизуем систему следующим образом. Вместо разделения всей популяции на N видов матриц, введем новую систему N квазивидов. Каждому квазивиду соответствует популяционная переменная y_i, которая является линейной комбинацией исходных популяционных переменных x_i, причем их сумма, конечно, не изменяется:

• К 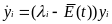аким образом выполнить это новое подразделение, подсказывает структура дифференциальных уравнений . Оно соответствует аффинному преобразованию системы координат, хорошо известному из теории линейных дифференциальных уравнений. Аффинное преобразование одного евклидова пространства в другое сохраняет параллельные прямые параллельными, а пересекающиеся – пересекающимися. Для трансформированных популяционных переменных y_i получим новую систему уравнений:

• П 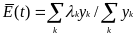рименение этой процедуры к нелинейным уравнениям возможно благодаря тому, что член, ответственный за нелинейность, E(t), согласно уравнению , остается инвариантным при трансформации и теперь может быть выражен как среднее всех λ_i

• Величины λ_i являются собственными значениями линейной динамической системы уравнений. Они, как и собственные векторы, которые связывают x_i с у_i, могут быть получены из матрицы, состоящей из коэффициентов W_ii и w_ik.

• Физический смысл решений системы относительно переменных y_i следующий: любой квазивид, собственное значение λ_i которого лежит ниже порога — среднего E(t) — будет вымирать, поскольку скорость изменения его численности отрицательна. И наоборот, численность каждого квазивида с λ_i выше порога будет расти. Однако, порог E(t) является функцией времени и будет расти.

• Рост будет происходить потому, что система благоприятствует квазивидам, которым соответствуют бОльшие собственные значения. Этот процесс будет продолжаться до тех пор, пока средняя продуктивность не сравняется с максимальным собственным значением и система не достигнет стационарного состояния. В этом стационарном состоянии в системе останется только один квазивид – тот, которому соответствует максимальное собственное значение, все остальные окажутся вымершими. Их популяционные переменные должны обратиться в ноль.

• Квазивид, как мы видим, понятие вполне теоретическое, полученное из математических моделей. Каков же физический смысл квазивида? Квазивид можно назвать «диким типом» популяции связанных друг с другом мутационным процессом молекул. В популяционной генетике обычно полагают, что дикий тип — это «стандартный» генотип, который в распределении генотипов в популяции соответствует оптимально адаптированному фенотипу. Однако лишь малая доля последовательностей полностью идентична той, которая считается диким типом.

• Большинство последовательностей являются копиями с одной или несколькими ошибками, и только среднее по распределению этих копий адекватно последовательности дикого типа. Численные эксперименты показывают, что стандартные копии (дикий тип) могут составлять меньше нескольких процентов всей популяции. Подавляющая часть популяции состоит из нестандартных копий (мутантов), более или менее далеких от дикого типа. При этом каждый конкретный мутант (нестандартная копия), по сравнению со стандартной копией, присутствует в этом распределении в очень малом количестве.

• Тогда полное распределение характеризуется некоей усредненной последовательностью, которая и определяет дикий тип. Квазивид, таким образом, представляет собой такое организованное распределение, которое характеризуется одной (или несколькими) усредненными последовательностями. Единственная усредненная последовательность имеется в единственном же случае - если стандартная копия явно доминирует. Явное доминирование выражается в том, что она имеет максимальную селективную ценность в пределах данного распределения.

• Те мутанты, у которых W_ii очень близки к максимальным значениям, будут (в среднем) присутствовать в популяции в бОльших количествах. Эта неравномерность приведет к тому, что последовательность дикого типа будет «недоопределена» в некоторых позициях, т.е. некоторые символы в последовательности будут определяться неоднозначно. Два близкородственных мутанта могут иметь практически одинаковые селективные ценности, тогда оба они будут входить в квазивид с почти равными статистическими весами.

• Эти мутанты могут стать селекционно неразличимы, если значения W_ii для них будут достаточно близки.

• Насколько близки друг к другу должны быть значения W_ii для этих двух мутантов, чтобы они стали селекционно неразличимы, зависит от их «степени родства». Ясно, что соответствие W_ii для отдаленно родственных последовательностей должно быть гораздо более точным, чем для копий с одной ошибкой.

КАТАСТРОФА МУТАЦИОННЫХ ОШИБОК

• Поскольку любой процесс репликации последовательности происходит с ошибками (мутациями), то это приводят к появлению квазивидов, представляющих из себя автономные группы последовательностей, мутационно переходящих друг в друга. Как было показано, устойчивость квазивидов - обязательное условие устойчивости ансамблей, в которые они входят. Кроме того, квазивиды, участвующие в циклических системах (гиперциклах, сайзерах) стабилизируются. Последовательность, составленная из наиболее вероятных символов в каждой позиции, называется "консенсусом" некоей группы последовательностей (квазивид в частности).

• Устойчивость консенсуса обеспечивает устойчивость квазивида.

• Э йген и Шустер показали, что длина оптимальной матрицы (v_m), средняя вероятность мутирования на позицию (1- ) и параметр отбора матрицы (σ_т)связаны неравенством

• Будем считать матрицу, имеющую наибольший параметр отбора, оптимальной. В таком случае, возможные длины последовательностей оказываются ограниченными сверху величиной v_max. Нарушение этого неравенства называется "катастрофой мутационных ошибок". Можно выделить три режима эволюции по отношению к границе катастрофы ошибок.

• 1) Квазивид далек от границы катастрофы ошибок (1- << 1/v_max). В этом случае скорость эволюции низка, от интенсивности отбора зависит слабо. При стабилизирующем в квазивиде присутствуют несколько близких (родственных) последовательностей, в том числе и оптимальная, которая доминирует. При движущем отборе оптимальная последовательность достигается медленно.

• 2) Квазивид находится вблизи порога катастрофы ошибок (1- < 1/v_max). Тогда, в среднем, каждая копия в каждом поколении имеет одну ошибку. Однако порог не нарушен, и скорость эволюции близка к максимальной. Доля оптимальной последовательности мала. Консенсус становится "идеальной" характеристикой квазивида в том сиысле, что он существует и устойчив, но не обязательно совпадает с какой-либо реально существующей последовательностью.

• 3) Порог катастрофы ошибок нарушен

• (1- > lnσ_m/v_max). В этом случае у квазивида нет ни устойчивого консенсуса, ни стационарной структуры, он подвержен случайным флуктуациям. Фактически квазивид в этом случае просто не существует.

• Судя по всему, ограничения на длину последовательности в силу неточного воспроизведения, неоднократно имели место в ходе как добиологической, так и биологической молекулярной эволюции. Ясно, что на ранних этапах добиологической эволюции вероятность ошибок репликации должна была быть очень велика. Из экспериментальных данных известно, что ошибки комплементарного узнавания нуклеотидов без участия ферментов репликации, 1- ~10^-2.

• Соответственно, размер матриц ограничен v_max ~10², мономеров. При появлении ферментов репликации граница отодвигается до ~ 10³ - 10⁴. Возникновение репарационных механизмов коррекции ошибок репликации у прокариот увеличивает v_max до ~ 10⁶ - 10⁷ (E.coli и др.). Формирование у эукариот механизмов репарации повреждений генома, а также диплоидности, повышает эту границу до ~ 10¹² -10¹⁴

• Такой подход имеет общеэволюционное значение - понятие консенсуса квазивида аналогично понятию нормы, постоянно используемому в популяционной и эволюционной генетике. Известны понятия видовой нормы, медицинской нормы, дикого типа и пр. Виды и популяции гетерогенны (если только это не лабораторные «чистые линии»), однако на основе совокупности наиболее часто встречаемых признаков видового уровня появляется представление о норме.

• Можно определить видовую норму как набор признаков, наиболее характерных для вида. Так называемая норма может быть идеальной конструкцией, т.е. реальных носителей нормы в популяции нет, но до тех пор пока она устойчива, мы можем говорить о существовании вида.

• Палеонтологи проводят оценки длительности существования видов основываясь на соображениях сохранение видовой нормы. Так, например, длительность существования видов животных и растений оценивается в

~ 1-30 млн лет. Далее появляются отличия от исходных форм по видовой норме морфологических признаков.

• Итак, динамика консенсуса квазивида является в некотором смысле молекулярной моделью динамики видовой и популяционной нормы. При этом норму можно рассматривать как консенсус изменяющихся признаков, которые характерны для рассматриваемого вида или популяции.

Теория нейтральной эволюции Кимуры. Режимы макроэволюции.

• Детерминированные модели динамики популяций

• Стохастические модели динамики популяций

• Связь параметров микроэволюционного и макроэволюционного процессов

• Генетический груз и дилемма Холдейна

• Скорости макроэволюции и роль многоклеточности

ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ ДИНАМИКИ ПОПУЛЯЦИЙ

• Под динамикой популяции будем понимать изменение во времени частот аллелей в популяции. Рассмотрим менделевскую (наследование признаков происходит по законам Менделя), бесполую, диплоидную (организмы имеют двойной набор хромосом), панмиктическую (могут скрещиваться все со всеми) популяцию с одним диаллельным локусом (А₁, А₂), где отбор осуществляется на уровне гамет.

• Пусть гаметы имеют приспособленности w₁ и w₂, соответственно, а разница приспособленностей s=w₁-w₂. Примем за p частоту аллеля А₁. Тогда мы можем записать детерминированное уравнение динамики

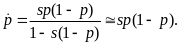
• У этого уравнения две тривиальные равновесные точки: = 0, = 1 и = 1, = 0.

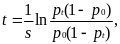При s > 0 устойчива первая, в этом случае предпочтительный аллель А₁, вытеснит аллель А₂ из популяции, при s < 0 – устойчива вторая и в популяции победит аллель А₂. Пусть р₀ - начальная частота аллеля А₁, а p_t - частота в момент t, тогда прямое интегрирование уравнения дает

• Из чего видно, что время достижения частоты p_t обратно пропорционально селективному преимуществу s адаптивного аллеля. Рассмотрим эту же задачу, но будем считать, что отбор осуществляется на уровне не гамет, а диплоидных особей. Обозначим приспособленности трех возможных генотипов A₁A₁, А₁А₂ и А₂А₂ через w₁₁, w₁₂ и w₂₂ соответственно.

• С 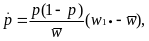оответствующее дифференциальное уравнение динамики для частоты аллеля А₁ имеет вид

где

w_1• = w₁₁p + w₁₂(1-p),

w_2• = w₂₁p + w₂₂(1-p),

а

= w_1•p+w_2• (1-p) = w₁₁p² + 2w₁₂p(1-p) + w₂₂(1-p)²

Из полученных выражений видно, что, если w₁₁> w₁₂ > w₂₂ , то устойчива равновесная точка = 1, = 0. В этом случае более приспособленный аллель А₁ вытесняет аллель А₂ из популяции. Если пересчитать приспособленность на гаметы, окажется, что аллель А₁, в любой момент в среднем более адаптивен, чем А₂:

w_1• > w_2•

• В случае w₁₁ < w₁₂ < w₂₂ картина противоположная.

• Е 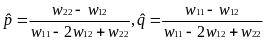сли w₁₁ < w₁₂, и w₂₂ < w₁₂, то есть идет отбор в пользу гетерозигот (в генотипе присутствуют два разных аллеля), то будет устойчива нетривиальная равновесная точка, описывающая полиморфизм, с частотами аллелей

• При описании дизруптивного отбора, т.е. ситуации, когда приспособленность больше у гомозигот (в генотипе присутствуют два одинаковых аллеля), что выражается в неравенствах w₁₁> w₁₂ и w₂₂ > w₁₂, полиморфная точка неустойчива и служит сепаратриссой – границей раздела двух зон устойчивости вокруг мономорфных точек

= 0, = 1 и = 1, = 0.

Описанные выше модели демонстрируют зависимость фазового портрета пространства частот от различных вариантов отбора особей с дифференциальной адаптивностью аллелей.

Теория нейтральной эволюции Кимуры. Режимы макроэволюции.

• Детерминированные модели динамики популяций

• Стохастические модели динамики популяций

• Связь параметров микроэволюционного и макроэволюционного процессов

• Генетический груз и дилемма Холдейна

• Скорости макроэволюции и роль многоклеточности

• Под динамикой популяции будем понимать изменение во времени частот аллелей в популяции. Рассмотрим менделевскую (наследование признаков происходит по законам Менделя), бесполую, диплоидную (организмы имеют двойной набор хромосом), панмиктическую (могут скрещиваться все со всеми) популяцию с одним диаллельным локусом (А₁, А₂), где отбор осуществляется на уровне гамет.

• Пусть гаметы имеют приспособленности w₁ и w₂, соответственно, а разница приспособленностей s=w₁-w₂. Примем за p частоту аллеля А₁. Тогда мы можем записать детерминированное уравнение динамики

• У этого уравнения две тривиальные равновесные точки: = 0, = 1 и = 1, = 0.

При s > 0 устойчива первая, в этом случае предпочтительный аллель А₁, вытеснит аллель А₂ из популяции, при s < 0 – устойчива вторая и в популяции победит аллель А₂. Пусть р₀ - начальная частота аллеля А₁, а p_t - частота в момент t, тогда прямое интегрирование уравнения дает

• Из чего видно, что время достижения частоты p_t обратно пропорционально селективному преимуществу s адаптивного аллеля. Рассмотрим эту же задачу, но будем считать, что отбор осуществляется на уровне не гамет, а диплоидных особей. Обозначим приспособленности трех возможных генотипов A₁A₁, А₁А₂ и А₂А₂ через w₁₁, w₁₂ и w₂₂ соответственно.

• Соответствующее дифференциальное уравнение динамики для частоты аллеля А₁ имеет вид

где

w_1• = w₁₁p + w₁₂(1-p),

w_2• = w₂₁p + w₂₂(1-p),

а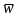

= w_1•p+w_2• (1-p) = w₁₁p² + 2w₁₂p(1-p) + w₂₂(1-p)²

Из полученных выражений видно, что, если w₁₁> w₁₂ > w₂₂ , то устойчива равновесная точка = 1, = 0. В этом случае более приспособленный аллель А₁ вытесняет аллель А₂ из популяции. Если пересчитать приспособленность на гаметы, окажется, что аллель А₁, в любой момент в среднем более адаптивен, чем А₂:

w_1• > w_2•

• В случае w₁₁ < w₁₂ < w₂₂ картина противоположная.

• Е сли w₁₁ < w₁₂, и w₂₂ < w₁₂, то есть идет отбор в пользу гетерозигот (в генотипе присутствуют два разных аллеля), то будет устойчива нетривиальная равновесная точка, описывающая полиморфизм, с частотами аллелей

• При описании дизруптивного отбора, т.е. ситуации, когда приспособленность больше у гомозигот (в генотипе присутствуют два одинаковых аллеля), что выражается в неравенствах w₁₁> w₁₂ и w₂₂ > w₁₂, полиморфная точка неустойчива и служит сепаратриссой – границей раздела двух зон устойчивости вокруг мономорфных точек

= 0, = 1 и = 1, = 0.

Описанные выше модели демонстрируют зависимость фазового портрета пространства частот от различных вариантов отбора особей с дифференциальной адаптивностью аллелей.

СТОХАСТИЧЕСКИЕ МОДЕЛИ ДИНАМИКИ ПОПУЛЯЦИЙ

• Те же задачи можно рассмотреть в стохастической постановке. Пусть имеется конечная менделевская панмиктическая популяция с постоянной эффективной численностью Ne = const. Изменение генетической структуры популяции происходит благодаря отбору гамет или особей.

• Единственный случайный фактор динамики популяции - биномиальный выбор 2Ne гамет при формировании следующего поколения. Данный популяционный фактор является одним из важнейших и может привести к серьезным последствиям. Стохастическим следствием случайного биномиального выбора гамет оказывается асимптотическая фиксация и утрата аллелей

• Е 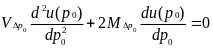сли рассмотреть процесс стохастической динамики частот аллелей в популяции как аналог диффузионного процесса, то в этом приближении его можно описывать прямым и обратным уравнениями Колмогорова. В частности, при изучении вопроса об асимптотической фиксации аллелей обычно используют стационарное обратное уравнение Колмогорова

• В этом уравнении: и(р₀) — условная вероятность асимптотической фиксации аллеля А₁, если eго начальная частота равна р₀ , — математическое ожидание изменения его частоты за поколение, a — дисперсия случайного изменения его частоты за поколение.

• Если предположить, что единственным случайным фактором в процессе жизни и размножения популяции является биномиальный выбор аллелей при формировании зигот следующего поколения, тогда

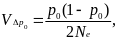
• а в качестве используются правые части соответствующих детерминированных уравнений динамики

• В 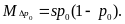случае гаметного отбора имеем

• В 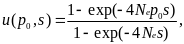таком случае, вероятность асимптотической фиксации аллеля А₁ (решение уравнения Колмогорова ) будет имеет вид

• Среднее время до фиксации t₁(р₀) выглядит достаточно сложно, поэтому приведем его только для некоторых существенных частных случаев.

• Например, рассмотрим ситуацию, когда аллель А₁ нейтрален по отношению к А₂ (т. е. s = 0), а начальная частота аллеля А₁ р₀ = 1/2N_e , т. е. А₁ – единственный в популяции (возник как мутация)

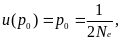
Тогда вероятность асимптотической фиксации аллеля А₁

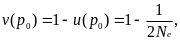
вероятность его случайной утраты

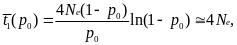
• среднее время до фиксации (исключая случаи утери аллеля)

а среднее время до случайной утери

С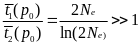 оотношение этих величин

• Таким образом, для 2Ne ≈ 10⁴, t₁(р₀) ≈ 2•10⁴ поколений, t₂(p₀) ~ 18 поколений, а на одну фиксацию приходится ~2Ne ≈ 10⁴ случайных утрат.

• Ясно, что вероятность фиксации адаптивного аллеля

u(p₀,s) > u(p₀),

а

(p₀,s) < (p₀) при s>0 и р₀ = 1/2Ne

• В то время, как для инадаптивного аллеля соотношения противоположные:

u(p₀,s) < u(p₀),

(p₀,s) > (p₀) при s<0 и р₀ = 1/2Ne

• Р 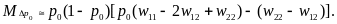ассмотрим стохастический вариант проанализированной выше детерминистической задачи об отборе на уровне генотипов особей. В этом случае

Величины же u(p₀,s), t₁(p₀,s) можно подсчитать только численными методами.

• Диаллельный случай отбора генотипов может быть качественно сведен к анализу пересчитанных приспособленностей гамет. Поэтому задача о гаметном отборе, хотя она и крайне упрощена как в детерминистическом, так и в стохастическом вариантах, может служить ориентиром при проведении анализа задачи стохастической фиксации аллелей при эволюции макромолекул.

• В результате, можно сделать вывод, что микроэволюционные стохастические процессы в популяциях конечной численности относительно редко заканчиваются фиксацией одних аллелей и относительно часто потерей других. При этом стохастические флуктуации частот аллелей становятся существенными в течение количества поколений, сравнимых с эффективной численностью популяций.

t ≥ 2Ne

• Этот вывод – один из наиболее важных результатов теории нейтрального генетического дрейфа - теории нейтральной эволюции Кимуры. Его можно использовать (и используют) для объяснения механизмов эволюции макромолекул.

СВЯЗЬ ПАРАМЕТРОВ МИКРОЭВОЛЮЦИОННОГО И МАКРОЭВОЛЮЦИОННОГО ПРОЦЕССОВ

• Кимура считал, что завершенные процессы микроэволюции (фиксации замен и т. д.) можно считать элементарными событиями макроэволюции. Фактически ему первому удалось связать параметры микро- и макроэволюции, используя разработанную теорию нейтрального генетического дрейфа.

• Первичные структуры аллельных и гомологичных генов и белков различны, они имеют фиксированные замены отдельных мономеров. Эти фиксированные замены отдельных мономеров, которые не затрагивают остальных мономеров последовательности, являются элементарными макроэволюционными различиями. Однако же, аллели и гомологичные гены большей частью сохраняют сходство между собой.

• Аллели, фиксированные на промежуточных этапах макроэволюции, редко исчезает бесследно. Обычно аллели-потомки имеют в своей первичной структуре (последовательности) ранее фиксированные замены мономеров.

• Фиксация аллеля означает, что все аллели-потомки хранят в своей первичной структуре эти фиксированные замены. При этом в популяции могут существовать и дугие аллели – другие варианты гена.

• Определим макроэволюционный процесс как последовательность стохастических фиксаций замен, происходящих в предыдущих аллелях из-за мутаций. Большинство из возникающих замен теряется, поэтому полное число замен должно быть много больше количества фиксируемых. Тогда для i-го локуса скорость фиксации замен с адаптивным преимуществом s = w₁ - w₂ будет равна

• K_i(s) = 2N_e μ_i(s) u(p₀,s)

• где в правой части стоит комбинация микроэволюционных параметров: N_e — эффективная численность популяции, μ_i(s) — плотность вероятности мутирования i-го гена в аллели с селекционным преимуществом s в единицу времени, а и(р₀, s) — вероятность асимптотической фиксации уже возникшего аллеля,

• Эти микроэволюционные параметры определяют величину K_i(s), которая является важнейшим макроэволюционным параметром. Таким образом, скорость фиксации замен определяется мутационным процессом, отбором и интенсивностью генетического дрейфа.

Для одиночно возникшей нейтральной мутации

р₀ = 1/2Ne, s = 0, и u(p₀,s) = р₀ = 1/2Ne,

откуда

K_i(0) = μ_i(0),

• т. е. скорость фиксации нейтральных мутаций определяется только скоростью их возникновения. Суммарная скорость фиксации всех адаптивных и нейтральных замен для i-го локуса будет

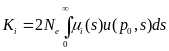
• Как показывают дополнительные исследования, дилемма Холдейна не возникает для нейтральных или почти нейтральных мутаций, т. е. отсутствуют ограничения на число одновременно эволюционирующих генов. В отличие от адаптивных мутаций выборочная случайная фиксация нейтральных аллелей не влияет на приспособленность и никак не изменяет скорость воспроизводства популяции.

Концепцию нейтральной эволюции Кимура и Ота сформулировали в виде 5 принципов:

1. Скорость эволюции белка (число аминокислотных замен на позицию в год) остается почти постоянной пока трехмерная структура и функция серьезно не изменены.

2. Более функционально значимые части молекулы белка (или целые молекулы) меняются путем замен медленнее, чем менее значимые.

3. Замены меньше искажающие структуру и функцию макромолекул фиксируются в эволюции много чаще.

4. Появлению гена с новой функцией обязательно должна предшествовать дупликация гена-предшественника.

5. Дарвиновский отбор заведомо предпочтительных мутантов происходит в процессе эволюции редко, много чаще происходит случайная фиксация слабодефектных и нейтральных мутантов, а также удаление заведомо вредных.

ГЕНЕТИЧЕСКИЙ ГРУЗ И ДИЛЕММА ХОЛДЕЙНА

Введем меру интенсивности генетического отбора – величину, которая представляет собой отношение разности между средней приспособленностью популяции и приспособленностью оптимального генотипа к приспособленности последнего. Под оптимальным генотипом будем понимать наиболее приспособленный. Эта мера будет описывать генетический груз популяции. Чем ближе средний уровень приспособленности к оптимальному, тем меньше генетический груз.

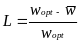
• Генетический груз L определяется следующим образом

где - средняя приспособленность популяции,

а - приспособленность оптимального генотипа.

• Собственно, под грузом можно понимать слабо приспособленные геномы, имеющие относительно большое количество «вредных» генов. Проблема существования и увеличения генетического груза оказалась одной из трудностей в развитии селективной теории генетики популяций и микроэволюции.

• Для очень большой диплоидной популяции со случайным скрещиванием, Холдейн показал, что при появлении полностью рецессивных вредных мутаций в аутосомном локусе, соответствующее снижение приспособленности равно скорости мутирования на гамету. Для полудоминантных мутаций груз равен скорости мутирования на зиготу.

• Причем груз почти не зависит от степени вредности мутаций. При других условиях, накладываемых на популяцию, локус и мутации, эти закономерности несколько модифицируются. Например, в случае очень малых популяций, в которых частоты мутаций дрейфуют от равновесных значений, оказывается, что в этих популяциях груз значительно выше, чем в больших

• Несколько упрощая формулировки, дилемма Холдейна заключается в том, что популяция с ограниченной скоростью воспроизводства не может быстро эволюционировать по многим генам одновременно.

• Холдейн показал математически, что даже в случае однозначного соответствия ген-признак в популяции не может заменяться одновременно свыше 12 генов «более приспособленными» аллелями без того, чтобы ее репродуктивная численность не стала исчезающее малой. Однако изучение природных популяций показало, что полиморфные популяции отличаются по очень большому числу аллелей, а вообще у организмов могут быть тысячи аллелей.

• Таким образом, согласно Холдейну, для поэтапной реализации таких различий природе потребовалось бы значительно больше времени, чем это в ряде случаев реально наблюдается. Дилемма Холдейна, демонстрирующая противоречие теории с экспериментальными данными, была частично разрешена лишь М. Кимурой, создавшего теорию нейтральной эволюции, которая основана на отказе от идеи исключительно селективной природы популяционных процессов.

СКОРОСТИ МАКРОЭВОЛЮЦИИ И РОЛЬ МНОГОКЛЕТОЧНОСТИ

Одноклеточные и многоклеточные организмы имеют разные характерные эффективные численности и среднее время жизни особей, т.е. характерную длительность поколения. Насколько многоклеточность особей влияет на скорость фиксации замен? Чтобы исследовать этот вопрос рассмотрим упрощенную модель

• Сравним две популяции:

• а) одноклеточную, имеющую эффективную численность 2N_e, длительность поколения τ, темп мутирования в класс адаптивности (s) на поколение μ_τ(s), вероятность асимптотической фиксации и(р₀, s) и скорость фиксации замен за поколение K_τ(s).

• Будем исходить из положения, что все фиксируемые мутации принадлежат какому-то одному классу адаптивности (s). Тогда

K_τ(s) = 2N_e μ_τ(s) u(p₀,s)

• б) многоклеточную, имеющую соответствующие параметры

2N_e*, τ*, μ*_τ* (s*), и*(р*₀, s*),

для нее

K*_τ*(s*) = 2N*_e μ*_τ*(s*) u*(p*₀, s*).

• Будем считать, что длительность поколения τ* = т τ, где т — число клеточных поколений по генеративной линии в ходе онтогенеза. Также предположим для простоты, что мутационные параметры клеток и одноклеточных, и многоклеточных организмов за цикл репликации одинаковы.

• Поскольку многоклеточные особи имеют время развития в m раз больше одноклеточных, то темп их мутирования в класс адаптивности

(s = s*) за поколение μ*_τ*(s)= m μ_τ (s). Поделив соответствующие выражение друг на друга, получаем

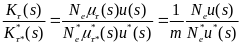
• Скорости фиксации замен выражаются через время, измеряемое в поколениях. Длительность поколения для одноклеточных и многоклеточных различна: τ и τ* соответственно. Однако мы можем пересчитать скорости фиксации замен на одинаковые единицы времени, например на время τ.

• Д 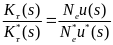ля этого достаточно взять K*_τ(s) = K*_τ*(s)/m. В результате имеем

П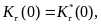 редположим, что фиксирующиеся мутации нейтральны в обеих популяциях, т.е. s = s* = 0. Тогда и = p_о = 1/2N_e, и* = p_о* = 1/2N*_e

т. е. скорости фиксации нейтральных замен в популяциях одноклеточных и многоклеточных особей одинаковы.

П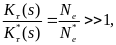 редположим, что фиксирующиеся мутации одинаково адаптивны: и ≈ 2s = u* ≈ 2s*. В этом случае и не зависит от N_e, поэтому получаем

По данным популяционной экологии, для популяций высших млекопитающих принимается N_e≈ 10⁴, тогда как для прокариот и одноклеточных N_e > 10⁸

Т. е. скорость фиксации адаптивных замен в единицу времени у многоклеточных на много порядков ниже, чем у одноклеточных.

Даже, если допустить некоторые различия между параметрами мутирования на репликацию, а также между и и и*, то этот вывод сохранится.

• Полученный результат достаточно прост, однако он демонстрирует чрезвычайно важное стохастическое свойство развития живых форм на Земле. А именно, при переходе от одноклеточных к многоклеточным происходит резкое замедление темпа фиксаций именно адаптивных мутаций при сохранении прежнего темпа фиксаций нейтральных замен. Это замедление связано с резким падением численности популяций, замедлением воспроизведения и т. п.

• Видимо, для компенсации этого существенного ограничения (в том числе) многоклеточные системы приобрели новые или усилили старые (по сравнению с одноклеточными) механизмы изменчивости и комбинаторики генов, мРНК и белков. К этим механизмам можно отнести дублирование генов, интрон-экзонную структуру, транспозоны, множественные повторы, альтернативный сплайсинг, множественные старты трансляции, микроРНК, модификацию белков и т.д.

• Ясно, что следствия резкого замедление темпа фиксаций именно адаптивных мутаций в многоклеточных организмах по сравнению с одноклеточными должны особенно сильно проявляться при их непосредственном контакте - например в экосистемах «паразит — хозяин».

МОЛЕКУЛЯРНАЯ КОЭВОЛЮЦИЯ В СИСТЕМЕ «ФАГ - БАКТЕРИЯ»

• Существование огромного потенциального разнообразия эквифункциональных вариантов генов и белков определяет возможность одного из режимов эволюции — синонимического дрейфа, т. е. случайной фиксации изменений структуры макромолекул без изменения их функции.

• Учет неизбежной смены условий существования популяций (смены экологических ниш) и связанных с этим изменений критериев отбора привел к представлению, что адаптивность (приспособленность) аллелей в конкретных нишах не обязательно коррелирует с глобальной (длительной) адаптивностью.

• В результате возможны следующие варианты макроэволюционного процесса: а) локально адаптивный, но глобально не направленный (когда адаптивность предыдущего аллеля в соответствующей экологической нише не соответствует другой нише); б) локально адаптивный и глобально направленный процесс (когда при смене аллелей и переходе от ниши к нише функция гена в целом совершенствуется, приобретаются новые, глобально адаптивные свойства).

• Основная трудность в проверке и использовании формулы Кимуры применительно к природным популяциям состоит в том, что неизвестно распределение по классам приспособленности, а также, что имеются лишь очень смутные представления о последовательности смены экологических ниш, которая влияет на микроэволюционные параметры: эффективная численность популяции, классы приспособленности и т.д.

• Однако для экосистемы фаг — бактерия такие оценки, хотя и приблизительно, можно сделать. Коэволюционирующая экосистема «вирулентный фаг - бактерия» отражает реальную эволюционную ситуацию, когда экологические условия, принципы отбора и способы размножения популяций фага и бактерии предельно просты и измеримы и эволюционный процесс протекает существенно быстрее, но принципиальные особенности процесса макроэволюции сохранены.

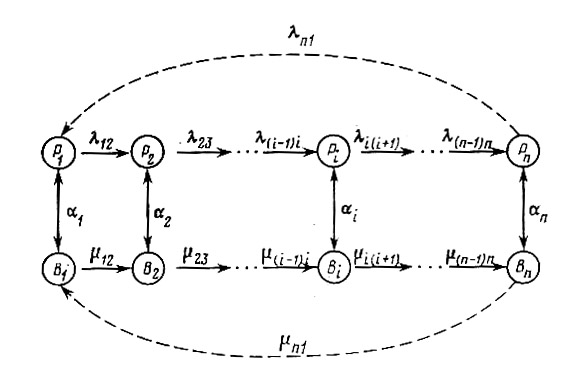
• Схема модели коэволюции контактирующих белков в системе фаг-бактерия. Обозначения: В₁, В₂,…, В_i, …, В_n – ряд штаммов бактерий, возникающих один из другого за счет мутирования в локусе белка рецепции; Р₁, Р₂,…, Р_i, …, Р_n - соответствующий ряд штаммов фага, вирулентных к бактериям с тем же номером. Пара <B_i , P_i > (i = 1,n) – обычная система «хищник-жертва»; m_i(i+1) – скорость мутирования из i-го штамма бактерии в (i+1)-й штамм; l _i(i+1) – соответствующая скорость мутирования у фагов; a_i – константа скорости адсорбции i-го фага на i-й бактерии.

• В центре экологических отношений двух популяций (фага и бактерии) оказывается их способность к взаимной рецепции — адсорбции, которая реализуется путем специфического соответствия двух белков: белка рецепции у бактерий и белка адсорбции у фагов. Элементарными событиями макроэволюции естественно считать возникновения и фиксации замен нуклеотидов и аминокислот, поскольку это есть фиксация аллелей соответствующих генов в популяциях клеток E.Coli и бактериофага. Замена аминокислоты в белке рецепции нарушает связывание фага с бактерией, адекватная замена аминокислоты в белке адсорбции восстанавливает паразитические возможности фага.

МОЛЕКУЛЯРНАЯ КОЭВОЛЮЦИЯ В СИСТЕМЕ «ФАГ - БАКТЕРИЯ»

• Как показывает исследование соответствующих математических моделей, эволюция данной экосистемы складывается из колебаний концентраций бактерии и фага (с очень большой амплитудой), при этом в каждом следующем цикле участвуют новые мутантные штаммы жертвы-бактерии и хищника-фага.

Кинетика концентраций фага и бактерии в детерминированной модели

• Эволюционная смена пар мутантных форм в экосистеме фаг-бактерия. x₀=1, y₀=1; α =0.3•10^-7 , β =0.3, частоты мутантов: 10^-5 для бактерий, 10^-7 для фагов. По оси абсцисс отложено время (t), измеряемое в числе поколений, звездочками отмечены моменты появления мутантов.

• Период колебаний на графике составляет 21—22 поколения — это и есть среднее время фиксации мутаций. С учетом сказанного выше его можно поделить на два периода: 1) период «ожидания» (17—18 генераций), в течение которого мутантные клетки, имея низкую частоту, «ожидают» того момента, когда экологическая ниша изменится таким образом, что они окажутся предпочтительнее предшествующего варианта, и 2) период собственно ф и к с а ц и и, длящийся всего три-четыре генерации, когда за счет тотального лизиса исходного штамма мутантные клетки автоматически повышают свою частоту до 1.

• Это и есть модель локально адаптивной, но глобально ненаправленной коэволюции. При этом скорость процессов настолько велика (на фиксацию нового аллеля требуется ~25 поколений, т.е. около суток), что по фактическому масштабу времени это типичный микроэволюционный процесс, хотя по сути, как уже говорилось, - макроэволюционный.

• При дефиците ресурса, потребляемого бактерией для своего роста, модель «вирулентный фаг - бактерия» становится коэволюционно неустойчивой. Однако систему может "спасти" от вырождения приобретение фагом определенного адаптивного усложнения своей молекулярно - генетической системы управления - приобретения свойства умеренности. «Умеренность» означает появление у фага механизма выбора между литическим (убивающим бактерию) и лизогенным (встраиванием генома фага в хромосому бактерии) режимами развития, который как раз и связан с оценкой уровня ресурсов размножения бактерии.

• Исследование условий существования и устойчивости состояний равновесия системы «умеренный фаг - бактерия» позволяет сделать следующие выводы.

• При недостаточном обеспечении бактерий ресурсом реализуется устойчивое лизогенное состояние равновесия, когда в зависимости от начальных концентраций фагов и бактерий имеются либо только лизогенные клетки, либо смешанная популяция из здоровых и лизогенных клеток. В обоих случаях благодаря интеграции генома фага с геномом бактерии сохраняется целостность системы как таковой.

• Напротив, если система хорошо снабжается ресурсом, можно гарантировать существование и устойчивость лишь одного равновесного состояния – литического, при котором фаг убивает (лизирует) всю популяцию бактерий. Литическое состояние не означает, однако, гибель системы, поскольку именно при богатом ресурсе есть возможность коэволюции за счет возникновения новых мутантных пар фаг-бактерия

• Нетривиальное равновесие, когда в системе имеются и зараженные фагом, и здоровые бактерии, и свободные фаговые частицы, существует в среднем интервале значений ресурса. Очевидно, что если этот интервал узок, нетривиальное состояние равновесия стуктурно неустойчиво.

• Таким образом, в основе развития системы "умеренный фаг- бактерия" на популяционном уровне лежит триггерный механизм - система имеет два устойчивых состояния: лизогенное при дефиците ресурса и литическое при его избытке. В лизогенном состоянии система не вырождается благодаря сохранению паразита в виде профага, а в литическом - за счет гарантированного возникновения новой пары мутантных штаммов-антагонистов, т.е. коэволюции.

• Невырождения данной системы можно добиться и «более простым» способом: введя проток всех компонент через резервуар. Исследование системы, описывающей динамику одной пары штаммов вируса и бактерии, показывает, что при биологически реалистичных значениях параметров системы наиболее вероятным устойчивым состоянием является нетривиальное равновесие с сохранением и фага, и бактерии, т. е. с невырождением системы как таковой.

• Изучение процесса появления мутантов по белкам рецепции – адсорбции показывает, что наличие протока приводит к полиморфизму как наиболее вероятному состоянию системы фаг — бактерия. В этой связи отметим, что фактически проточная модель фаг — бактерия представляет собой интересный пример зависимости вероятности фиксации мутаций в одних генах (определяющих эффективность адсорбции) от мутаций в других генах (определяющих скорость воспроизведения).

• Реальные системы могут, очевидно, быть попеременно то проточными, то непроточными. Образно говоря, ситуация напоминает смену сухого сезона сезоном дождей. «Сухой сезон» отвечает изолированному резервуару, «сезон дождей» — проточному. Им соответствует качественное изменение режимов эволюции. В изолированном резервуаре при избытке ресурсов возможна устойчивая коэволюция популяций вирулентного и умеренного фага и бактерии.

• При ограниченном ресурсе — лизогенное состояние системы умеренный фаг — бактерия. В проточном резервуаре коэволюция фага и бактерии невозможна — устанавливается сбалансированный полиморфизм пар мутантных вариантов. А в целом такая смена внешних условий переводит систему из микроэволюционно стабильного состояния полиморфизма в стабильный режим коэволюции и обратно

МОЛЕКУЛЯРНАЯ ЭВОЛЮЦИЯ ИММУННОЙ СИСТЕМЫ

У высших позвоночных (рептилий, птиц, млекопитающих) эта система представляет собой целый комплекс мультигенных семейств (МС), кодирующих молекулы иммуноглобулинов (ИГ) и других ИГ-подобных иммунных рецепторов. Дифференциальная экспрессия МС и определяет принадлежность иммуннокомпетентных клеток к тому или иному функциональному типу. В целом весь этот сложный ансамбль МС функционирует так, чтобы обеспечить две основные функции иммунной системы: достаточно точное опознание и ликвидацию любого чужеродного антигена (АГ), не важно эндо- или экзогенного происхождения.

ВИРУСНАЯ ИНФЕКЦИЯ КАК ФАКТОР ПРОГРЕССИВНОЙ ДИВЕРГЕНЦИИ ИММУННОЙ СИСТЕМЫ В ХОДЕ ЭВОЛЮЦИИ

• Одним из факторов, относительно которого следует оценивать адаптивность конкретных особенностей молекулярной организации иммунной системы, являются инфекционные микроорганизмы и прежде всего вирусы и бактерии. Этот фактор относится к числу эволюционно наиболее древних, постоянно действовавших факторов

• В контексте проблемы анализа возможных селективных факторов прогрессивной эволюции (от более простой к более сложной) иммунной системы особенно интересной представляется ситуация, когда вирусы и другие инфекционные микроорганизмы (микобактерии, простейшие и т.п.) в качестве мишени поражают непосредственно клетки самой иммунной системы.

• Для иммуноцитов современных позвоночных таких инфекций известно немало: лимфоцитарный хориоменингит, полимиелит, грипп, лейкемия Френда, алеутская болезнь норок; инфекции вызванные цитомегаловирусом мышей, вирусами Денге-2, простого герпеса и т. п. Широко известен вирус — возбудитель СПИДа (AIDS). По-видимому, любая популяция или субпопуляция клеток иммунной системы может стать прямой мишенью для подобных инфекций.

• Математическая модель именно таких инфекций, в которых некий «обобщенный» вирус (любая внутриклеточная инфекция) поражает клетки некой эволюционно древней иммунной системы, позволяет выяснить, существуют ли (и какие) способы противостоять столь опасным для организма-хозяина инфекциям

• Модель рассматривает гипотетический предковый организм с примитивной, слабо дифференцированной иммунной системой. Предположим, что соответствующие предковые иммунные клетки (пралимфоциты) в процессе онтогенеза переходят из состояния незрелости (незрелые пралимфоциты - НП) в зрелое состояние (зрелые пралимфоциты – ЗП). Всюду в дальнейшем будем говорить о вирусных инфекциях данной иммунной системы, имея, однако, в виду, что и любые другие инфекции (см. выше) подобного рода описываются таким же образом.

• Предположим также, что вирусы способны поражать только клетки НП, т. е. незрелые пралимфоциты. Будем считать при этом, что молекулярно-генетическая система иммунитета предельно проста, а именно для адсорбции вирус использует тот самый рецептор клетки НП, которым клетки типа ЗП в свою очередь опознают и инактивируют вирусы. Адсорбция вируса на НП ведет к образованию зараженных клеток из которых путем лизиса выходят дочерние вирусы частицы. Связывание ЗП с вирусом, напротив, приводит к уничтожению вирусов.

• Эта разница в свойствах клеток ЗП и НП может быть объяснена различными способами. Например, пралимфоциты могли обладать способностью фагоцитировать вирусные частицы, но зрелые клетки разрушали их с помощью нуклеаз или/и протеаз, а в незрелых клетках соответствующие ферменты либо еще не синтезировались, либо были неактивны.

• Возможна в некотором роде обратная ситуация, когда зрелый пралимфоцит «сбрасывает» с поверхности связанный с вирусом рецептор, избегая тем самым заражения и инактивируя вирус.

• Данная модель описывает процессы, в общем аналогичные тем, которые происходят в тимусе млекопитающих или в бурсе птиц. И в том, и в другом органе предшественники лимфоцитов, пришедшие из костного мозга, размножаются и созревают в отсутствие антигенов. Зрелые лимфоциты секретируются наружу и заселяют периферические лимфоидные органы. Однако в целом модель не описывает современную иммунную систему высших позвоночных, а является описанием лишь тех простых систем защиты, которые могли существовать на ранних этапах эволюции.

• И 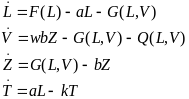так, рассмотрим гипотетический предковый организм с примитивной, слабо дифференцированной иммунной системой. Обозначив символами L, V, Z, Т концентрации соответственно незрелых пралимфоцитов, вирусов, зараженных клеток и зрелых пралимфоцитов, запишем следующую систему дифференциальных уравнений динамики:

• Здесь F(L)—функция, описывающая скорость размножения незрелых пралимфоцитов. Количество локальных минимумов и максимумов не ограничено, хотя из биологических соображений наиболее правдоподобно выглядит «одногорбый» вид функции F(L). Функция G(L, V) описывает скорость заражения незрелых пралимфоцитов L вирусами V. Явный вид функции G(L, V) может быть, например, таким: G(L, V)=cLV, c>0.

Примерный вид функций F(L) и G (L, V)

• Будем анализировать устойчивость к малому возмущению особых точек систем, где все производные равны нулю. Нетривиальные точки покоя, где концентрации всех компонент положительны, не рассматриваются, поскольку отражают состояние хронической болезни, которая рано или поздно все равно кончается либо гибелью, либо выздоровлением организма-хозяина, и именно эти крайние альтернативные состояния в основном и оценивает естественный отбор.

• Система имеет полутривиальные точки покоя: I — (0, , 0, 0), — произвольное (может быть =0);

II — ( , 0, 0, ), где = a/k , a — корень уравнения F(L)=aL

• Первая точка соответствует состоянию «смерти» популяции пралимфоцитов в очаге инфекции, вторая – здоровому состоянию организма.

• Анализ локальной устойчивости точки I показывает, что, если в очаге заражения накопилось мало вирусов и/или они недостаточно инфекционны, а скорость размножения незрелых пралимфоцитов достаточно велика, то поступление извне в очаг инфекции новых клеток типа L позволит им размножиться и восстановить популяцию

• Л окальная устойчивость или неустойчивость точки II системы имеет биологический смысл устойчивости или неустойчивости этой пралимфоидной ткани против малой инфекции. Естественно предположить, что организм, улучшающий свою устойчивость против инфекции, получает селективное преимущество.

• Точка II устойчива, если

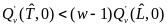и неустойчива, если

Случай строгого равенства не рассматривается по причине его биологической нереальности.

• Таким образом, увеличения устойчивости состояния II (фактически состояния «здоровья») можно достигнуть за счет увеличения значения Q_V^'( , 0) и/или уменьшения значения G_V^'( , 0).

• Значение w зависит от вируса и, по предположению, не изменяется иммунной системой. В свою очередь усиление связывания вирусов зрелыми пралимфоцитами (Q_V^'( , 0)) может быть достигнуто как увеличением стационарной концентрации , так и увеличением сродства рецепторов клетки Т к вирусу V. Аналогичным образом ослабить связь вирусов с незрелыми пралимфоцитами (G_V^'( , 0)) можно как через уменьшение стационарной концентрации , так и снизив сродство рецепторов клетки L к вирусу V

• Однако поскольку единственным источником зрелых пралимфоцитов являются незрелые, то при уменьшении будет уменьшается и . Для увеличения же необходимо увеличивать , причем как видно из рисунка, <L*, т. е. ограничено сверху

• Таким образом, в рамках данной модели единственным удачным решением проблемы стало бы приобретение рецепторов L и Т с различной авидностью к V. По сути дела это означает, что необходимо обеспечить пралимфоцитам смену АГ-специфичных рецепторов в процессе онтогенеза, причем у рецепторов, экспрессирующихся позднее, специфичность к АГ должна быть выше.

• Возможность стимулированной АГ пролиферации зрелых пралимфоцитов вывода не меняет, как показывает исследование соответственно модифицированной модели. Все приведенные выше рассуждения остаются в силе и в более сложном случае, когда вирус несет сразу несколько АГ-детерминант и соответственно защитная система пралимфоцитов способна на каждую АГ-детерминанту вируса реагировать специфичным клоном.

• Таким образом, к сравнительно просто организованной иммунной системе, отвечающей ранним этапам ее эволюции, предъявляются требования взаимно исключающие друг друга. С одной стороны, чем точнее будет опознаваться чужеродный (например, вирусный) АГ, тем эффективнее будет происходить инактивация этих вирусов с помощью соответствующих рецепторов пралимфоцитов, но с другой — чем эффективнее идет адсорбция вируса на пралимфоцитах-мишенях, тем больше опасность их гибели.

• Повысить устойчивость пралимфоидной системы к малой инфекции можно (в рамках указанных упрощений) двумя способами. Первый — через увеличение количества клонов пралимфоцитов, специфичных к разным АГ-детерминантам, второй — путем изменения авидности АГ-специфичного рецептора в ходе созревания пралимфоцитов.

• В рассмотренном случае рецепторы должны быть похожи друг на друга, но не слишком: похожи, чтобы зрелый пралимфоцит как можно лучше опознавал вирус, не слишком, чтобы вирус как можно хуже опознавал незрелый пралимфоцит. Второй способ представляется особенно действенным в условиях слабодифференцированной иммунной системы, способной опознавать ограниченный круг АГ-детерминант.

• Обе эти возможности были реализованы в процессе эволюции. Наличие большого числа АГ-специфичных клонов лимфоцитов у современных высших позвоночных — факт, признаваемый всеми современными теориями иммунитета. У мыши, например, насчитывается ~10⁸ клонов В-лимфоцитов разной специфичности

• Второй способ фактически означает, что в адсорбции вирусов на иммуноцитах-мишенях и вместе с тем в опознании вирусов (вирусных АГ) с последующей их инактивацией и разрушением не могут участвовать в точности идентичные рецепторные молекулы: организм может справиться с инфекцией только тогда, когда эти функции будут выполнять гомологичные, но не идентичные ИГ-подобные белки.

• Следовательно, стратегическим решением проблемы для жертвы являются мультипликация генов ИГ-подобных рецепторов и последующая коадаптивная дивергенция соответствующих МС на новые подсемейства. В ответ вирусы вынуждены изменяться так, чтобы приобрести способность адсорбироваться на новых иммунорецепторах (и, следовательно, инфицировать новую популяцию иммунных клеток-мишеней).

• В отличие от ранее рассмотренного режима локально адаптивной, но ненаправленной молекулярной коэволюции в простых экосистемах типа «фаг — бактерия», данный вариант коэволюции представляет собой глобально направленный и адаптивный процесс прогрессивного усложнения иммунной системы.

ВНУТРЕННИЕ ПРИЧИНЫ ПРОГРЕССИВНОЙ ЭВОЛЮЦИИ ИММУННОЙ СИСТЕМЫ.

• Рассмотрим в качестве биосистемы иммунную систему и будем исходить из предположения, что любая отдельная клетка может активироваться для действий по определенной программе (для выполнения которой она и предназначена), но в отсутствие реального сигнала к активации. Будем называть это событие для краткости спонтанной активацией (СA).

• Произойти это может по многим причинам: мутация, заражение вирусом и пр. Подобная спонтанная активация представляет собой "сбой программы" и некоторым образом аналогична злокачественному перерождению клетки. Эта аналогия особенно отчетливо просматривается на примере иммунной системы, т.к. активация компетентного иммуноцита для уничтожения АГ подразумевает и его (иммуноцита) пролиферацию, т.е. ускоренное размножение

• Чтобы любая такая спонтанная активация клетки была ощутима для организма, необходимо, чтобы сложная система обладала тремя свойствами:

• 1) большое количество клеток- в системе должно быть достаточно много клеток, чтобы событие СА могло реально произойти;

• 2) усиление эффекта - система должна быть устроена таким образом, чтобы происшедшее на клеточном уровне даже единичное событие СА имело вполне ощутимые последствия на уровне организма, иначе это событие не будет замечено естественным отбором;

• 3) отсутствие эффективной отрицательной обратной связи - конечный продукт ответа на какой-либо раздражающий сигнал не должен эффективно ингибировать начальные стадии собственного синтеза.

• Рассмотрим в качестве объекта СА В-лимфоцит. Предположим, что покоящийся В-лимфоцит спонтанно (неантигенно) активировался и начал синтезировать антитела к отсутствующему реально АГ. В пользу того, что такое событие может произойти, говорит факт существования миелом - опухолей иммунной системы, при развитии которых клеточный клон В-лимфоцитов не поддается межклеточной регуляции, бесконтрольно размножается и в избытке образует специфические антитела только одного типа

• Поскольку частота злокачественного перерождения оценивается как 10^-6, то можно считать, что частота спонтанной активации (СА) В-клетки в отсутствие АГ не ниже, чем 10^-6. Насколько большой вред может нанести организму подобное событие?

• Если принять частоту СА В-клетки за 10^-6, то в организме мыши, например, должны одновременно пролиферировать в отсутствие стимулирующеего их АГ более 200 В-лимфоцитов (что количественно эквивалентно примерно 20 клонам)

• Таким образом, если в организме мыши спонтанно активировавшиеся В-клетки дойдут до стадии плазмоклетки (синтезирующей огромное количества молекул иммуноглобулина), то их суммарный иммунный ответ "ни на что" будет таким, каким был бы ответ на примерно 20 АГ-детерминант.

• Для человека ситуация аналогичная, но, естественно, с большими количествами клеток. Ясно, что в реальных иммунных системах имеются "предохранители" от подобных нежелательных эффектов. Появление в эволюционном прошлом субпопуляции Т-хелперов могло оказаться одним из основных таких "предохранителей".

• Схема основных взаимодействий клеток иммунной системы при гуморальном иммунном ответе

• Неактивированный В-лимфоцит (обозначен В₀), после встречи с антигеном (AG) и получение дополнительного сигнала от T-хелпера (T_h) переходит в состояние В_μ (синтез молекул иммуноглобулина М (IgM), специфичных к AG). T-хелпер (T_h) получает сигнал от AG посредством антигенпредставляющей клетки (чаще всего макрофага). Кроме того, T-хелпер (T_h) помогает В_μ –лимфоциту перейти в стадию В_γ, когда происходит переключение на активный синтез иммуноглобулина G (IgG) высокоспецифичного к AG. Попутно образуются клетки памяти Вm, активирующиеся при вторичном заражении тем же AG. Из состояния В_γ лимфоцит переходит в стадию В_p – плазмоклетки или антителобразующей клетки (АОК). В этой стадии синтезируется огромное количество высокоспецифичного к AG иммуноглобулина G.

• В схеме на рисунке опущено множество деталей, поскольку для наших рассуждений существенно лишь то, что для перехода от стадии покоя к стадии АОК В-лимфоциту требуется двойной сигнал: первый непосредственно от АГ, второй - от Т-хелпера. В то же время известно, что для дифференцировки, например, эритроидной клетки- предшественника, представляющей собой не менее сложный процесс, чем антигензависимое созревание В-лимфоцита, достаточно одного сигнала, представляемого эритропоэтином.

• Однако Т-хелпер тоже получает сигнал к активации от АГ. Таким образом, сигнал фактически раздваивается: связав АГ и интернализировав его, антигенпредставляющие клетки представляет АГ-детерминанты Т-хелперу, который, активировавшись, секретирует различные лимфокины (регуляторные молекулы иммунной системы) и, тем самым, дает В-клетке дополнительный сигнал, идущий в конечном счете, от антигена же.

• Зачем нужен второй сигнал, почему бы В-клетке не проходить весь путь от стадии покоящейся клетки до АОК, проконтактировав только с АГ?

• В свете изложенных выше соображений легко увидеть, что если бы этот «oднocигнaльный», путь был реализован, то в организмах с большим количеством эффекторных лимфоцитов с широким спектром специфичностей события СА могли бы приводить к достаточно частым неприятностям.

• Приобретение в процессе эволюции системы Т-хелперов и, соответственно, необходимость дополнительного сигнала от них для последующего развития минимизируют негативные последствия для организма от случаев СА.

• Клетки-регуляторы, подавляющие иммунный ответ, не могут эффективно ингибировать спонтанно активировавшийся лимфоцит-эффектор, если они АГ- специфические, т.к. в этом случае АГ отсутствует и они не инициируются к супрессии. Если же эти клетки-регуляторы АГ- неспецифические, то они должны (как это происходит в реальных иммунных системах) ингибировать лишь конечные стадии иммунного ответа (чтобы не мешать нормальному иммунному ответу на реальный антиген) и, следовательно, не мешают и спонтанно активировавшимся лимфоцитам.

• Если мы предполагаем, что В-клетка может претерпевать СА, то такую же возможность следует предположить и для Т-хелперов. Однако, это никак существенно не влияет на ситуацию. Событие СА для Т-хелперов будет состоять в том, что клетка активируется и, в отсутствие реального АГ, начнет "помогать" переходу В₀-лимфоцита в стадию В_μ и в стадию В_γ.

• Если считать действие хелперных факторов неспецифичным относительно AГ (Т-хелпер, активированный одним АГ может "помочь" В-лимфоцитам активированным другими АГ), то в случае, если две спонтанно активировавшиеся клетки - В-лимфоцит и Т-хелпер окажутся достаточно близко друг от друга, В-клетка пройдет все стадии пролиферации и дифференциации вплоть до АОК. Однако вероятность этого события пренебрежимо мала

• Если же рассматривать "помощь" Т-хелперов как специфический процесс, то вероятность того, что два лимфоцита: Т- и В-клетки с одинаковой специфичностью спонтанно активируются одновременно и окажутся рядом друг с другом, представляется совершенно ничтожной.

• Всю вышеизложенную логику можно применить и к Т-клеточному иммунному ответу, где также через Т-хелперы передается второй сигнал от АГ к клеткам- предшественникам цитотоксических Т-клеток.

• Таким образом, по излагаемой гипотезе, организм, приобретший в своем эволюционном развитии иммунную систему состоящую из достаточно большого количества клеток, ставится перед фактом возможности СA своих эффекторных клеток. В этом случае приобретение подсистемы, ставящей "барьер" на пути ускоренного размножения и дифференциации СА клонов (в рассмотренном случае барьер заключается в отсутствии "помощи" от Т-хелперов) было бы явно адаптивно, поскольку минимизировало бы отрицательные последствия событий СА.

• При этом приобретение такой подсистемы стимулировалось бы свойствами самой системы - ее величиной и сложностью функционирования (при неизменных внешних условиях существования).

• Аналогичную "страховку" системы от случайных "сбоев" можно увидеть в организации нервных центров спинного мозга, т.е. центров, куда сходятся сигналы от периферийных рецепторов.

• Также "страховку" системы от случайных "сбоев" можно наблюдать и в социальных системах.

2 рис.

• Многократное превышение частоты фиксации одиночных замен по сравнению с делециями и вставками. Эта закономерность отчетливо просматривается и в эволюции других семейств белков.

• На одну делецию в реальных последовательностях приходится около 50 замен. 3 замены правдоподобнее 2-х делеций.

AEDN-R AEDNR

A-DNKR ADNKR

Ala Glu Asp Asn Arg

Ala Asp Asn Lys Arg

Адаптивное ускорение фиксации замен в эпоху выхода позвоночных животных на сушу (400-500 млн лет назад). 1 – в среднем по белку;

2 – центр контакта, α₁ – β₂; 3 – регуляторный центр связывания ДФГ(дифосфоглицератфосфат).

• Геном вируса гриппа, как известно, способен мутировать с исключительно высокими темпами благодаря неточностям при тиражировании своей наследственной информации. Частота нуклеотидных замен в его наследственном материале, РНК, в тысячи раз выше, чем та, что обнаружена для генома человека.

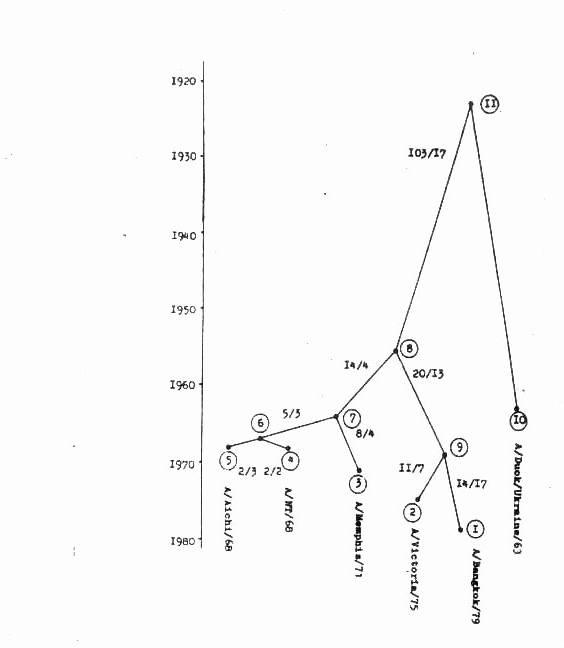
Филогенетическое дерево генов гемагглютинина H3 вируса гриппа типа А. "Висячие" вершины отвечают эпидемическим штаммам. Вблизи ветвей указаны числа синонемических/несинонемических замен.

Множественное выравнивание 17 случайно выбранных аминокислотных последовательностей внутреннего района ГА вирусов гриппа А, В, С. Звездочки обозначают аминокислоты, которые в данной позиции одинаковы во всех последовательностях. Многоточие – аминокислоты с аналогичными свойствами во всех позициях.

Филогенетические деревья, построенные для этих 17 последовательностей. Деревья построены различными методами. Около узлов – значения bootstrap показателей. Шкалы внизу – количество аминокислотных замен на сайт. Поддеревья подтипов (a) H1 и (b) H2 в филогенетическом дереве для 172 аминокислотных последовательностей внутреннего района HA вируса гриппа A. Вершины для которых оценены годы дивергенции отмечены черными кружками и буквами. Подчеркнуты человеческие и свиные последовательности, использованные для оценки скоростей и годов дивиргенции. Жирным выделены последовательности, использованные для оценки скоростей. Шкалы означают количество аминокислотных замен на сайт. Молекулярные механизмы, обеспечивающие взаимодействие вируса гриппа с клеткой-хозяином и дальнейшее его проникновение внутрь клетки, до сих пор остаются предметом многих научных исследований. Главная цель последних — помочь в разработке лекарственных препаратов, способных предотвратить инфицирование клетки вирусом. Что особенно актуально в связи с возможностью новой пандемии гриппа, причиной которой может стать мутированный штамм так называемого «птичьего» гриппа. Фактически исследуется молекулярная эволюция вируса гриппа.

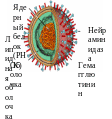
Схематичное представление вируса гриппа А. В центре вирусной частицы находится РНК, наследственный материал вируса, и ряд белков, необходимых ему на первых стадиях жизненного цикла в клетке хозяина. Гемагглютинин и нейраминидаза располагаются на поверхности вириона и отвечают за способность вируса проникать в клетку. Они же являются мишенями для B-клеточных антител, вырабатываемых иммунной системой инфицированного организма.

• Гемагглютинин и нейраминидаза отвечают за способность вирусной частицы проникать в клетку. При помощи гемагглютинина вирус прикрепляется к клетке, а фермент нейраминидаза разрушает клеточную мембрану, создавая условия для проникновения вируса внутрь клетки путем клеточного включения (эндоцитоза). Когда вирус попадает внутрь клетки, благодаря ионным каналам изменяется pH внутри вириона, что позволяет вирусу осуществить освобождение генетического материала из вирусной капсулы, предварительно проведя его подготовку.

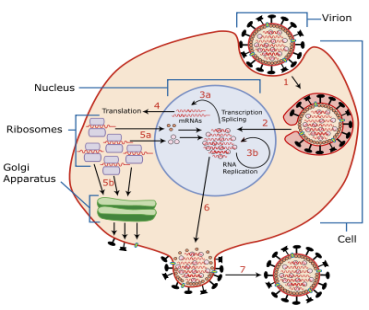• Таким образом, гемагглютинин играет одну из важнейших ролей при инфицировании вирусом клетки-мишени. На поверхности вирусной оболочки гемагглютинин присутствует в виде тримеров, т.е. комплексов, состоящих из трех молекул. Каждая его молекула, в свою очередь, состоит из двух субъединиц, одна из них обеспечивает первичный контакт с клеткой, а вторая отвечает за слияние с мембраной клетки. Процесс слияния сопровождается значительными перестройками молекулы гемагглютинина, при которых высвобождается пептид слияния, спрятанный во внутренней части глобулы белка.

• В вирусных белках можно выделить так называемые антигенные детерминанты — участки, с которыми предпочтительно связываются антитела. Мутации, вызывающие структурные изменения в подобных местах, т.е. меняющих форму и расположение антигенных детерминант, как раз и приводят к образованию новых вирусных штаммов. Такие вирусы становятся практически «невидимыми» для антител, уже циркулирующих в крови зараженного организма, что делает его безоружным перед нашествием вирусов.

• В отличие от других белков поверхность гемагглютинина в высокой степени обогащена местами посадки различных ионов. Еще одно не менее интересное свойство гемагглютинина — он содержит также большое число потенциальных мест такой посадки, которые могут превратиться в сайты связывания ионов в результате одиночной мутации, т.е. замены всего лишь одной аминокислоты.

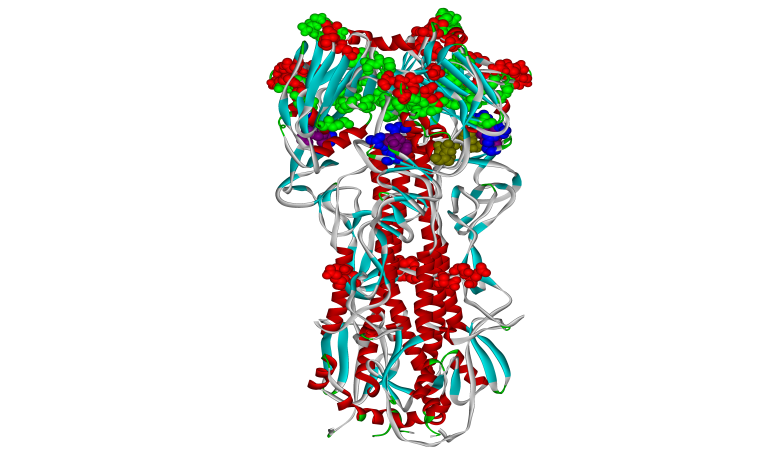• Сайты связывания различных ионов обнаруженные в пространственной структуре гемагглютинина вируса гриппа А (атомы аминокислот, формирующие сайт показаны шариками, цветом отмечены сайты связывания разных типов ионов). Благодаря этим сайтам вокруг вируса может формироваться своеобразный ионный щит, защищающий его от атак иммунной системы.

Примеры использования филогенетических методов

• Белок Р53

• Цитохромы Р450

• Прионы

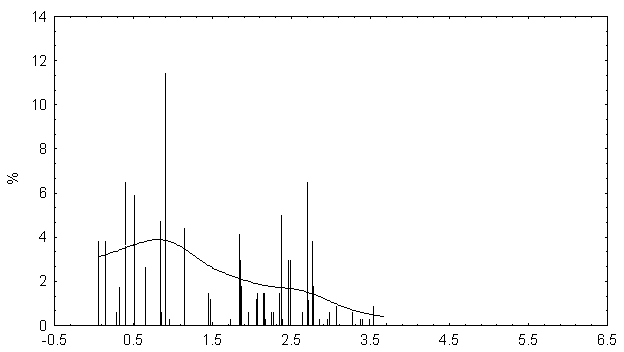
• Распределение значений физико-химических различий для аминокислотных замен для филогенетического спектра гена P53. По оси абсцисс - физико-химическое расстояние между аминокислотами (по матрице Мийяты). По оси ординат - число замен, в %

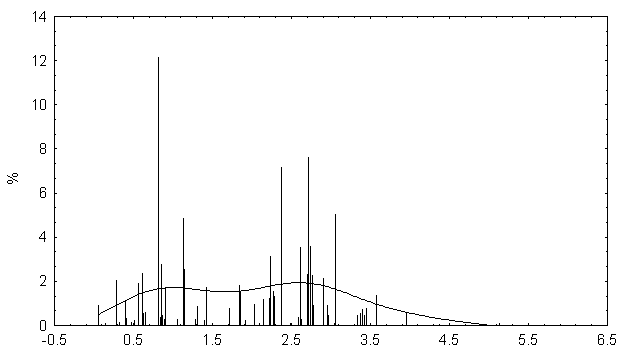
• Распределение значений физико-химических различий аминокислотных замен по базе данных канцерогенных мутаций гена P53.

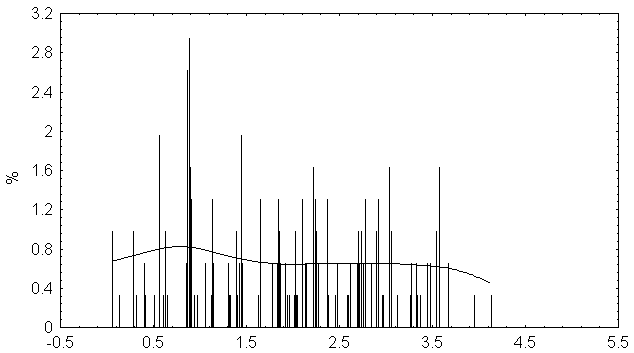
• Распределение значений физико-химических различий аминокислотных замен выявляемых при анализа псевдогенов гена P53.

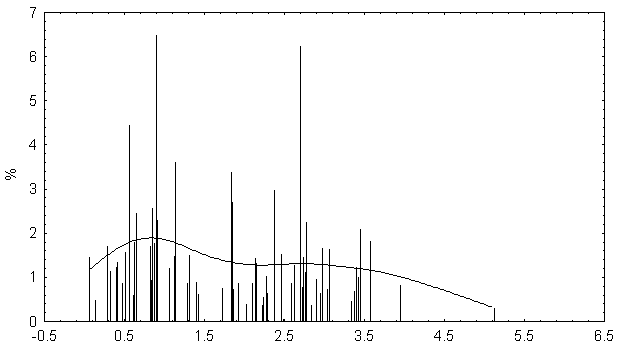
• Распределение значений физико-химических различий для аминокислотных при случайных генерациях для гена P53.

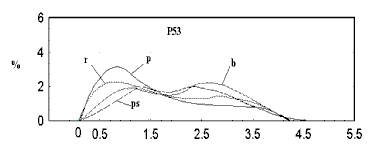
• Сравнение полиномиальных аппроксимаций распределений замен по физико-химическим-свойствам для гена P53. b - распределение для базы данных канцерогенных мутаций, p – для эволюционного мутационного спектра, ps – для мутаций в псевдогенах, r- для случайного мутационного спектра

• Распределение случайно сгенерированных мутаций в человеческом гене p53 близко к таковому в раковых клетках. Различие в средних значениях мало, но статистически значимо. Псевдогены и случайно сгенерированные последовательности того же самого состава дают существенно различающиеся распределения мутаций, особенно внутри важного ДНК-связывающего центрального участка p53.

• Полученные результаты свидетельствуют о том, что первичная структура центрального домена человеческого гена p53 имеет некоторую структурную предрасположеность к разрушающему мутагенезу. Любой из 4-х рассматриваемых спектров мутационных спектров p53 отчетливо отражает эту предрасположенность, особенно при отсутствии отрицательного давления отбора (как в p53 псевдогенах).

• Образование нового сайта связывания иона цинка в мутантном белке p53 человека, конкурирующим с нормальным сайтом за связывание цинка. Зеленым овалом отмечен нормальный сайт связывания иона цинка, красным – сформированный в результате мутации G245C.

• Цитохромы P450 - большое суперсемейство гем-содержащих, связывающихся с мембраной белков с молекулярным весом 50 000 DA (400-530 аминокислот). В суперсемействе насчитывается более 500 членов, относящихся к 85 эу- и 20 прокариотическим видам, и около 30 псевдогенов. Цитохромы P450 участвуют в окислительном метаболизме широкого класса экзо- и эндогенных веществ (стероидов, жирных кислот, простагландинов, лекарственных веществ, канцерогенов, мутагенов, всего более 80 веществ) у бактерий, грибов, растений и животных. Большинство членов этого суперсемейства классифицируется как неспецифические монооксигеназы.

• В пределах суперсемейства наблюдается довольно значительная внутри- и межвидовая вариабельность, что обуславливает полиморфизм по особенностям метаболизма токсичных внешних агентов и большое разнообразие субстрат-специфичности цитохромов P450. Предполагается, что эволюционное приобретение такого широкого спектра субстрат-специфичности стимулируется необходимостью детоксикации разнообразных внешних химических агентов

• Цитохромы семейств CYP11, CYP17 и CYP21 имеют прямое отношение к конгенитальной адренальной гиперплазии (КАГ), которая является одним из самых частых заболеваний человека и наследуется по аутосомно- рецессивному типу. Причиной заболевания является нарушение синтеза кортизола и альдостерона с одновременным накоплением андрогенов.

• Из 5 ферментов, необходимых для синтеза кортизола из холестерина, 4 являются цитохромами (семейства 11, 17 и 21). Их гены расположены на разных хромосомах. CYP11A и CYP11B - ферменты, активные в митохондриях, 17 и 21 - микросомные. Более 90% случаев КАГ являются результатом дефицита CYP21 различной степени выраженности, основная причина остальных случаев - нарушение функции CYP11.

• У человека ген CYP21 представлен в двух копиях - активный ген (CYP21, или CYP21B) и неактивный псевдоген (CYP21P, или CYP21A). Копии имеют 98% гомологии и образуют тандемный повтор. Псевдоген имеет несколько небольших делеций и аминокислотных замен. Близость расположения гена и псевдогена приводит к большой вероятности неравного кроссинговера при мейозе и, соответственно, генной конверсии. Около 20% случаев дефицита CYP21 связано с делецией значительной части или всего гена. Большая часть оставшихся мутантных аллелей имеет небольшие делеции или вставки

• Методами многофакторного анализа показано, что мутационные спектры семейств CYP1, CYP2, CYP11 и CYP6 близки друг к другу, тогда как спектры CYP7 и CYP21 отдалены от этих четырех. Все они вместе близки к глобинам и сильно отличаются от спектра прионовых белков

• Нормальные гены CYP21 цитохромов Р450 (5 видов). Зависимость числа замен от физико-химического расстояния между аминокислотами до и после замены

• Ненормальные аллели CYP21 цитохромов Р450 человека. Зависимость числа замен от физико-химического расстояния между аминокислотами до и после замены.

• Псевдогены CYP21 цитохромов Р450 человека. Зависимость числа замен от физико-химического расстояния между аминокислотами до и после замены.

• Полученные результаты не подтверждают распространенную гипотезу о переносе посредством генной конверсии мутаций, возникших в псевдогенах, в нормальные аллели гена CYP21, поскольку, как видно из рисунков, мутационные спектры ненормальных аллелей и псевдогенов существенно различаются: в псевдогенах слишком мало мутаций с теми параметрами, которых много в поврежденных аллелях, в частности в левом крае распределений. Скорее всего, источником мутаций в поврежденных генах могут быть нестабильные участки самого гена, а не генная конверсия с участием псевдогенов

• Согласно сушествующей гипотезе, прионовые белки существуют в двух изоформах: в виде нормального клеточного белка (обозначаемого PrPC), встраивающегося в клеточную мембрану, и в виде анормального белка (обозначаемого PrPSc), накапливающегося в мозговой ткани больных. Спектроскопический анализ PrPSc и PrPC показал, что они имеют различую конформацию: PrPC содержит »43% a-спиралей и практически не содержит b-складчатых структур, тогда как PrPSc имеет высокое содержание b-структур.

• Основываясь на некоторых экспериментальных данных, было предположено, что анормальный PrPSc каким-то образом может вызывать изменение конформации нормального PrPC, что препятствует встраиванию последнего в мембрану и способствует его накоплению в клетке

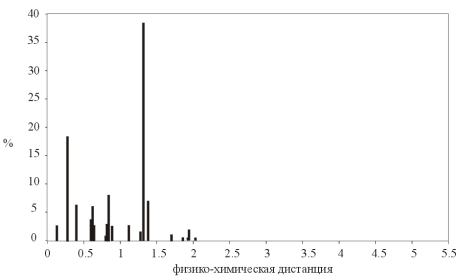
• Распределение частот встречаемости аминокислотных замен в зависимости от физико-химического расстояния между исходной и возникшей в результате замены аминокислотами. Данные для кодонов, входящих в участки Н1-Н4

• Распределение частот встречаемости аминокислотных замен в зависимости от физико-химического расстояния между исходной и возникшей в результате замены аминокислотами. Данные для части последовательности, не входящей в участки Н1-Н4.

• Таким образом, в прионовых белках, связанных с заболеванием, наблюдается выраженная тенденция к возникновению замен, нарушающих a-спиральность. Полученные данные подтверждают предположение о том, что в основе прионовых заболеваний лежит изменение конформации PrP с разрушением a-спиралей и образованием b-структур.

Роль отрицательного регуляторного контура при разных видах отбора.

• Биологические системы являются открытыми неравновесными системами, которые функционируют и воспроизводятся на основе обмена с окружающей средой потоками вещества, энергии и информации. К числу фундаментальных свойств биологических систем, независимо от уровня их сложности и особенностей организации, относится их способность к самовоспроизведению. Под самовоспроизводящейся будем понимать любую систему, способную к воспроизведению своих копий на основе содержащейся в ней наследственной информации.

• Одноклеточный про- или эукариотический организм представляет из себя СВ-систему минимального уровня сложности, способную к полностью автономному воспроизведению своих копий.

• Глобальными СВ-системами иерархически более высоких уровней являются биосфера Земли и ее ноосфера в понимании Вернадского

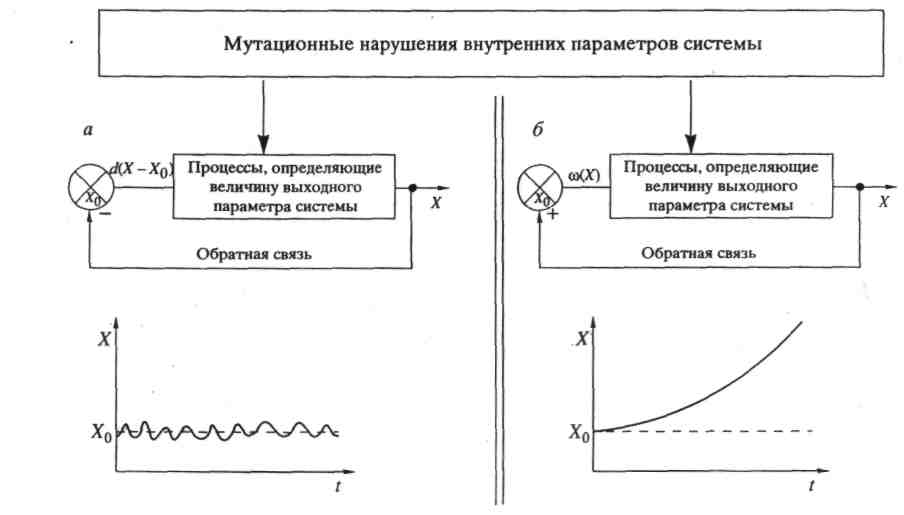• В СВ-системах имеются два типа регуляторных контуров: с положительной и отрицательной обратной связями

• Контур с отрицательной обратной связью предназначен для поддержания величины контролируемого признака X вблизи оптимального для данных средовых условий уровня Х0. Значение признака X измеряется системой рецепции и по информационному каналу передается в блок регуляции. В организмах в качестве информационных каналов используются потоки метаболитов, гормонов, медиаторов, нервных импульсов и т.д.

• Блок регуляции сравнивает текущее значение X с Х0 и продуцирует управляющий сигнал d(X - Х0). Если X значимо отклоняется от Х0, то управляющий сигнал корректирует процесс формирования признака и приближает X к оптимальной величине Х0.

• Функция контура с положительной обратной связью состоит в максимально эффективном отклонении контролируемого признака X от его исходного значения Х0 Положительные обратные связи обеспечивают быстрое самовозбуждение элементов эндокринной и нервной системы (что важно, в частности, для осуществления стрессовых ответов), а также играют ключевую роль в регуляции процессов морфогенеза, роста и развития организмов, по своему смыслу представляющих быстрый уход от первоначального состояния.

Роль отрицательного регуляторного контура при разных видах отбора.

• Как возникают и усложняются регуляторные системы в эволюции? Рассмотрим простейший контур с отрицательной обратной связью (ООС), регулирующий концентрацию белка. Любое отклонение концентрации белка от нормы отслеживается регуляторным звеном ООС, компенсирующим его, путем изменения скорости биосинтеза белка (эффекторное звено ООС). Причем контуру безразлична природа факторов, приводящих к отклонениям от нормы.

• Рассмотрим простейшую систему, в которой концентрация белка X в организме определяется двумя процессами: его биосинтезом и деградацией. Возмущающими воздействиями отклоняющими концентрацию белка от оптимального уровня Х0, являлись мутации, приводящие к понижению конформационной стабильности белка и как следствие - к увеличению его деградации.

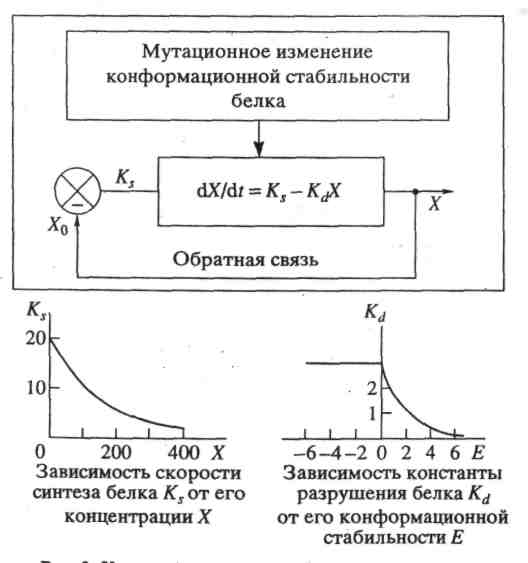
• Концентрация белка X описывается следующим уравнением:

dX/dt = К_s - K_dX,

где K_s и K_d - скорость синтеза белка и константа его деградации соответственно.

• Рассмотрены два варианта модели: с отрицательной обратной связью и без нее. В системе без обратной связи скорость синтеза белка постоянна, а в системе с обратной связью она зависела от концентрации белка. В рамках этой модели получены следующие основные качественные результаты.

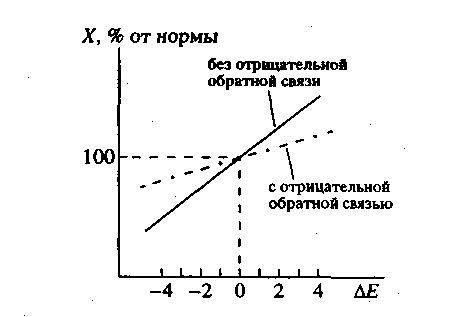
• На рисунке приведены зависимости равновесной концентрации белка от мутационного изменения стабильности, рассчитанные в варианте с отрицательной обратной связью и без нее.

• Итак, наличие в системе отрицательной обратной связи приводит к компенсации повреждающего эффекта мутаций. В данном случае это происходит за счет увеличения скорости биосинтеза белка при мутациях, увеличивающих скорость его деградации, и уменьшения скорости биосинтеза белка при мутациях, снижающих скорость его деградации.

• Суть эффекта состоит в том, что отрицательная обратная связь за счет компенсаторного изменения интенсивности регулируемых процессов минимизирует (маскирует) фенотипическое проявление мутаций. Таким образом, под влиянием отрицательных обратных связей происходит "обнейтраливание"мутационного спектра

• Мутационный спектр любого локуса (гена) характеризует распределение возникающих в нем мутаций по влиянию на приспособленность организма. Качественно можно выделить три основных класса возникающих мутаций: 1) повреждающие, 2) нейтральные, 3) адаптивные.

• Повреждающие мутации в ходе эволюции, как правило, фиксироваться не могут. Нейтральные мутации не влияют на приспособленность и могут фиксироваться в популяциях за счет генетического дрейфа. Адаптивные мутации могут фиксироваться в популяциях с весьма большой скоростью за счет положительного отбора.

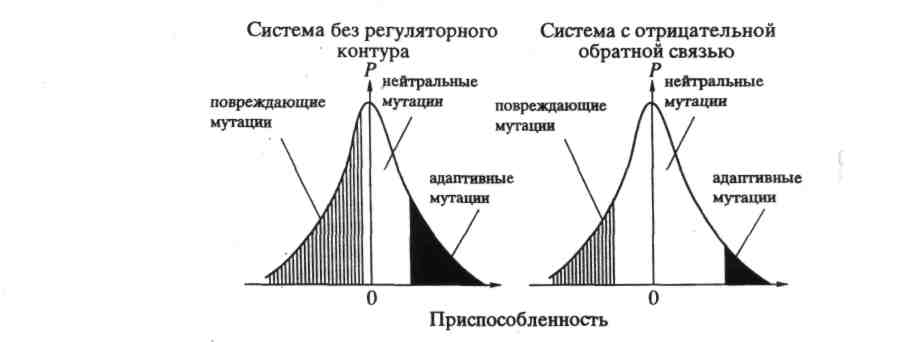
• В результате обнейтраливания в мутационном спектре уменьшается доля адаптивных и повреждающих мутаций, так как наличие отрицательной обратной связи уменьшает (маскирует) их фенотипическое проявление. Соответственно увеличивается доля нейтральных мутаций. Эффект обнейтраливания тем более выражен, чем более эффективным является контроль параметра по механизму отрицательной обратной связи.

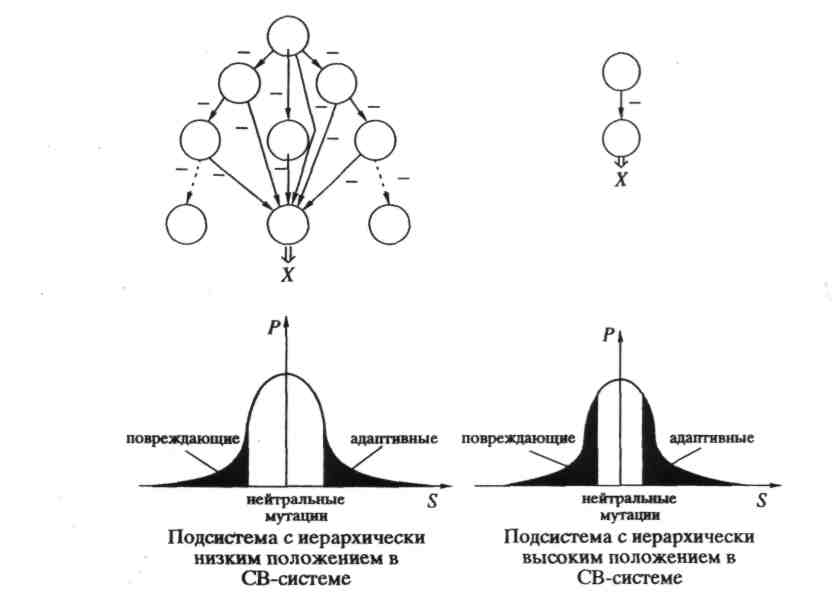
• Эффективность контроля параметра по механизму отрицательной обратной связи, в свою очередь, зависит от иерархического положения подсистемы, определяющей данный параметр, в составе СВ-системы. При низком иерархическом положении подсистемы она контролируется большим количеством отрицательных обратных связей от вышележащих подсистем, что должно приводить к более выраженному эффекту обнейтраливания. Напротив, при более высоком иерархическом положении, когда подсистема контролируется меньшим количеством отрицательных обратных связей от вышележащих подсистем, эффект обнейтраливания должен быть выражен слабее

• Таким образом, стабилизирующий и движущий/дизруптивный отборы противоположным образом влияют на регуляторные системы организмов, что приводит к так называемым эволюционным качелям. Поочередно при стабилизирующем отборе происходит возникновение и усиление ООС, а при движущем отборе - ослабление или разрушение некоторых ООС. Спектр мутаций, среди которых есть вредные, нейтральные, инадаптивные и адаптивные должен фиксироваться в геномах таксонов в период стазиса в нейтральном режиме.

• В процессе захвата новой экологической ниши (или изменения старой) происходит слом контура ООС и гиперманифестация изменчивости, после чего таксоны с вредными мутациями быстро вымирают, следом за ними в ходе отбора постепенно вымирают или вытесняются в другие экологические ниши таксоны с инадаптивными мутациями. Если это действительно так, то фиксация практически всего спектра адаптивных для новой ниши мутаций должна проходить за короткое время и именно в периоды заселения (формирования) новых экологических ниш, что подтверждают эксперименты.

Размеры геномов и плотность кодирования информации

• Различия в размерах геномов чрезвычайно велики. У мельчайших РНК-содержащих вирусов геном содержит лишь около 10³ н.п., а у водорослей и амфибий до 10¹¹ н.п.. Однако длины геномов лишь частично коррелируют с их функциональной нагрузкой и сложностью генных сетей соответствующих организмов. Под функциональной нагрузкой понимается общее количество генов, кодирующих и регуляторных РНК, белков. Размеры геномов в целом возрастают с усложнением организмов, т.е. с ростом сложности генных сетей.

• У вирусов, имеющих зависимую от хозяина и неполную генную сеть онтогенеза, минимальный размер генома равен 10³ н.п. (1 ген). Среди секвенированных на данный момент прокариот наименьший клеточный геном имеет Candidatus_Carsonella_ruddii_PV (182 гена, 159662 н.п.). Самая мелкая из микоплазм - Mycoplasma_genitalium имеет 580076 н.п., 477 генов и белков. Однако, микоплазма – паразит и ей нет нужды обеспечивать кодирование всех систем, выполняющих фундаментальные генетические процессы и контролирующих базовый метаболизм, клеточные структуры и функции.

• Среди эукариот наименьшие геномы имеют низшие грибы (~ 2•10⁷ н.п., ~ 10⁴ генов и белков). В отличие от одноклеточных у многоклеточных эукариот нет явной зависимости между сложностью организации и размером генома (так называемый C-value парадокс).

• Гаплоидные геномы четко подразделяются на классы по максимальной длине: РНК-геномы вирусов и фагов ~ 10⁴ н.п., ДНК-геномы вирусов и фагов ~ 5•10⁵ н.п., геномы бактерий ~ 2•10⁷ н.п., геномы низших грибов, имеющих длительную гаплоидную фазу ~ 2•10⁸ н.п. Скорее всего, эти ограничения на максимальную длину генома связаны с вероятностями мутирования, которые зависят от систем репарации клеток, разных в организмах разных классов.

• Плотность кодирования генетической информации весьма различна у про- и эукариот. Вирусы, фаги, бактерии, митохондрии, хлоропласты имеют высокую плотность кодирования информации. Т.е. доля некодирующих участков в геноме невелика (у фага λ ~ 17%), гены не дублированы, иногда даже перекрываются, а размеры геномов поэтому могут служить оценкой их информационной емкости. У E. coli K12 87,8% генома занимают реальные и вероятные белок-кодирующие гены; 0,8% - гены т-РНК, р-РНК и др.; 0,7% - некодирующие повторы; 11,0% генома - функциональные сайты и другие участки, выполняющие регуляторные и другие функции. Таким образом, геном E. coli K12 очень плотно нагружен генами (~ 88,5%), а межгенные участки занимают относительно малую долю (~11%).

• В геномах эукариот плотность кодирования информации гораздо более низкая. Кодирующей является <5% ДНК генома, а >95% составляют различные мобильные элементы, интроны, псевдогены и другие некодирующие участки. Как правило, некодирущие участки содержат множество повторов, мобильные генетические элементы также существуют в основном в очень многих копиях. Однако существует достаточно много данных, говорящих о том, что некодирующие участки, тем не менее, могут играть важную роль в регуляции функционирования генома.

• Кодирующая часть генома содержит мультигенные семейства и супергены, которые дублируют гены или их фрагменты. Степень дублирования может быть велика. На данный момент секвенировано несколько сотен геномов различных организмов (в основном одноклеточных). Полученная информация позволяет говорить о так называемом G-value парадоксе: геномы эукариот содержат гораздо меньше генов, чем ожидалось и количество генов плохо коррелирует со сложностью организма.

Блочно-модульная структура макромолекул

• Процесс биологической молекулярной макроэволюции не исчерпывается заменами мономеров и небольшими делециями и вставками. Эти процессы, в основном, обеспечивают синонимическую эволюцию последовательностей, т.е. сохраняют и совершенствуют функцию.

• Однако, существуют многочисленные факты, и их становится все больше, которые указывают, что основным источником новшеств на молекулярном уровне является блочно-модульная организация и комбинаторная изменчивость макромолекул. Фактически, прогрессивная эволюция – это эволюция сложности, причем сложность следует понимать как сложность и многообразие регуляций.

• Согласно принципу "тинкеринга", для создания новых функциональных блоков используются, в основном, функционирующие фрагменты уже существующих и работающих макромолекул. Этот принцип сформулирован Ф.Жакобом (Jacob, 1977) "Естественный отбор - действует как "умелец", который не знает точно, что собирается соорудить, но использует все, что попадается ему под руку".

• Из-за синонимической изменчивости каждый тип блока представлен множеством функциональных вариантов и каждый вариант продолжает нейтрально или адаптивно эволюционировать без порождения принципиально новых вариантов. В работе генных сетей эти варианты в принципе взаимозаменяемы именно благодаря изофункциональности. Скорее всего, путь "тинкеринга" - основной путь прогрессивной эволюции, особенно для сложных систем. Этот вывод основывается на необходимости выполнения общего требования непрерывности функционирования живой системы

• Тем не менее, случайные или слабо функциональные последовательности также могут эволюционировать благодаря изменчивости и селективному усилению слабых активностей, специфичностей структурных элементов и т.п., которые редко, но встречаются даже в случайных последовательностях макромолекул. Однако путь этот очень длинен, неэффективен для эволюционных приобретений широкого профиля и потому ограничен относительно небольшими последовательностями и простыми функциями.

Блочно-модульная эволюция иммунной системы

• Надсемейство иммуноглобулинов (IgSF) объединяет в своем составе белки, структурной особенностью которых является наличие одного или более Ig-подобных доменов. IgSF относится к наиболее многочисленным по составу надсемействам, а по структурному и функциональному разнообразию составляющих его членов не имеет аналогов.

• IgSF представляет собой яркий пример прогрессивной эволюции, связанной с множественными дупликациями одного предкового гена и является исключительно интересной моделью изучения основной проблемы макроэволюции – механизмов возникновения функциональных нововведений и их встраивания в предсуществующие сети белковых взаимодействий.

• Эволюция парных рецепторов иммунной системы, относящихся к FcR и KIR семействам.

Парные рецепторы разделены на два функциональных класса, ингибирующих и активирующих молекул. Считается, что они играют важную роль в регуляции иммунного ответа посредством изменения баланса разнонаправленных сигналов.

• На основании анализа геномов нескольких видов позвоночных, установлено, что парные рецепторы FcR и KIR семейств относятся к числу наиболее диверсифицированных групп белковых молекул.

• Во-первых, количество генов, кодирующих эти рецепторы у разных видов колеблется в пределах двух порядков величины, от десятка до полутора сотен.

• Во вторых, структура парных рецепторов отличается исключительным разнообразием. Хотя в составе белков разных видов позвоночных присутствуют родственные подтипы Ig-подобных доменов, доменные архитектуры рецепторов рыб, амфибий и млекопитающих совершенно различны.

Разнообразие доменной архитектуры белков FcR семейства.

• Схематичное изображена структура и композиция доменов белков FcR семейства человека, мыши, шпорцевой лягушки, пещерного сомика, корющки, данио и тетраодрона. Кружками показаны Ig-подобные домены, треугольниками – муцин-подобные домены, квадратом – SRCR-подобные. Прямоугольники со знаком + обозначают трансмембранные домены активирующих рецепторов, ассоциируемых с сигнальными трансмембранными субъединицами. Закрашенные прямоугольники – трансмембранные домены мономерных ингибирующих рецепторов. Линией условно изображены цитоплазматические участки рецепторов.

• Огромные различия обнаруживаются даже при сравнении видов, относящихся к разным отрядам одного класса. Филогенетический анализ показал, что основную роль в эволюции парных рецепторов играли видо-специфичные рекомбинационные процессы, обеспечившие постоянную перетасовку отдельных структурных модулей.

• Предполагается, что основной ролью этих белков являлось распознавание и связывание чужеродных микроорганизмов и, что физиологические роли, обнаруженные у некоторых парных рецепторов млекопитающих, являются относительно недавними функциональными нововведениями.

• Филогенетический анализ FcR-подобных генов четырех видов млекопитающих, курицы и лягушки показал, что разделение семейства на три функционально различающиеся группы - cFcR, FCRL, IFGP произошло после дивергенции млекопитающих и птиц, но до разделения плацентарных и сумчатых млекопитающих.

• В каждом из отрядов млекопитающих семейство эволюционировало видоспецифичным образом. Основными событиями были дупликации и потери генов, а также интенсивная межгенная и внутригенная перетасовка экзонов в FcR и IFGP подсемействах. В результате этих процессов каждый из изученных видов млекопитающих получил свой уникальный набор белков IFGP подсемейства.

• Особенно интересным примером является ген IFGP7, который кодирует мозаичный секретируемый белок, состоящий из четырех Ig-доменов и одного скавенжер-домена. Согласно филогенетическим реконструкциям, этот ген является продуктом рекомбинации между одним из предковых IFGP генов и геном CD5L, относящимся к надсемейству скавенжер рецепторов. Рекомбинация произошла у предка плацентарных млекопитающих после их отделения от сумчатых. Ген IFGP7, сохранился у хищных и грызунов, но был потерян приматами.