35.Матричний метод побудови множинної лін регресії
У
практиці часто виникають ситуації,
коли функція відгуку (цілі) Y
залежить не від одного, а від багатьох
факторів. Встановлення форми зв'язку
в таких випадках починають, як правило
з розгляду лінійної регресії такого
виду: У такому випадку результати
спостережень повинні бути представлені
рівняннями, отриманими в кожному з п
дослідів:
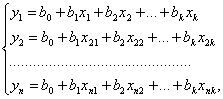(1)
або у вигляді матриці
результатів спостережень:
де
п
- кількість дослідів; k
- кількість факторів.
Для вирішення
системи рівнянь (1) необхідно, щоб
кількість дослідів було не менше
k
+ 1, тобто п
k
+ 1.
Завданням множинного регресійного
аналізу є побудова такого рівняння
прямої k-мірному
просторі, відхилення результатів
спостережень
від
якої були б мінімальними. Використовуючи
для цього метод найменших квадратів,
отримуємо систему нормальних рівнянь:
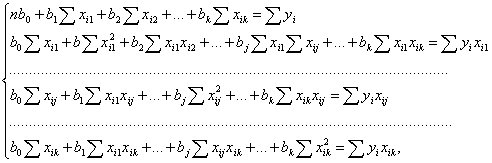яку
представимо в матричній формі
(Х
Т
Х) У
= X
T
Y,
(2)
де В
- вектор-стовпець коефіцієнтів рівняння
регресії;
X
- матриця значень факторів;
Y
- вектор-стовпець функції відкликання;
X
Т
- транспонована матриця X.
При
=
1,
,
Вони відповідно
рівні:
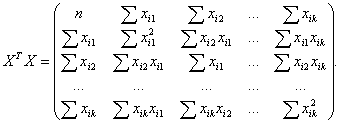Перемноживши
праву і ліву частину рівняння (2) на
зворотну матрицю (Х
Т
Х)
-1,
отримаємо при:
Кожен
коефіцієнт рівняння регресії обчислюється
за формулою:
де
-
Елементи оберненої матриці (Х
Т
Х)
-1.
Для перевірки значимості рівняння
регресії необхідно при заданих значеннях
(
)
Провести кілька експериментів, щоб
отримати деяке середнє значення функції
Y.
34.Типи кривих зростання.Методи лінеаризації
Лінеаризáція — (лат. linearis — лінійний), один з методів наближеного представлення замкнутих нелінійних систем, при якому дослідження нелінійної системи замінюється аналізом лінійної системи, в деякому розумінні еквівалентної початковій. Методи лінеаризації мають обмежений характер, тобто еквівалентність початкової нелінійної системи і її лінійного наближення зберігається лише при певному «режимі» роботи системи, а якщо система переходить з одного режиму роботи на іншій, то слід змінити і її лінеаризировану модель. Застосовуючи лінеаризацію, можна з'ясувати багато якісних і особливо кількісних властивостей нелінійної системи.
Методи:
1) Метод статистичної лінеаризації
Метод заснований на заміні нелінійного перетворення процесів статистично еквівалентними їм лінійним перетвореннями. Нелінійний елемент замінюється лінійним еквівалентом (рис.1). У результаті заміни система лінеарізуется, що дозволяє використовувати методи дослідження лінійних систем. Заміна нелінійного перетворення лінійним є наближеною і справедливою лише в деяких відносинах. Тому не існує однозначної еквівалентності при використанні різних критеріїв. Зокрема, якщо нелінійність визначається безінерційної залежністю виду v=y(x) використовується два критерії еквівалентності. Перший критерій передбачає рівність на виході нелінійного елемента і його лінійного еквівалента математичних сподівань і дисперсій процесів. Другий критерій - мінімум середнього квадрата різниці процесів на виході нелінійного елемента і його лінійного еквівалента.