
- •26 Линейные операторы. Собственные векторы и собственные значения линейных операторов.
- •2 7 Виды уравнений плоскостей и прямых в пространстве. Уравнения их параллельности и перпендикулярности.
- •28. Линии 2-го порядка
- •29. Поверхности 2-го порядка.
- •31.Многочлены над полями q,r,t. Основная tr алгебры.
- •32.Прямая на плоскости. Ур-е прямой на плскости в прямоугольной сис. Координат.
29. Поверхности 2-го порядка.
Общие
ур-я 2-го порядка имеют вид:

К числу поверхностей 2-го порядка относятся: эллипсоид, однополостный гиперболоид, двуполостный гиперболоид, эллиптический параболоид, гиперболический параболоид, конус, цилиндры.
Приведем канонические ур-я этих поверхностей:
э![]() ллипсоид:
ллипсоид:

Если
т. М(x,y,z)![]() эллипсоиду,
то ему также будут
точки: (-x,-y,-z),
(-x,y,z,),(x,-y,z),(x,y,-z),(-x,-y,z),а
это значит, что т. О(0;0;0) явл. центом
симметрии. Пл-ти ХОУ,ХОZ,YOZ
явл. пл-ми симметрии и координатные оси
явл. осями симметрии. Эллипсоид-
поверхность огранниченная.
эллипсоиду,
то ему также будут
точки: (-x,-y,-z),
(-x,y,z,),(x,-y,z),(x,y,-z),(-x,-y,z),а
это значит, что т. О(0;0;0) явл. центом
симметрии. Пл-ти ХОУ,ХОZ,YOZ
явл. пл-ми симметрии и координатные оси
явл. осями симметрии. Эллипсоид-
поверхность огранниченная.
однополостный
гиперболоид:
 .
.
 т.О(0;0;0)-
т. симметрии; координатные пл-ти
х=0,у=0,z=0
– пл-ти симметрии, оси x,y,z
– оси симметрии. Сечение гиперболоида
х=0 пл-тью есть гипербола:
т.О(0;0;0)-
т. симметрии; координатные пл-ти
х=0,у=0,z=0
– пл-ти симметрии, оси x,y,z
– оси симметрии. Сечение гиперболоида
х=0 пл-тью есть гипербола:
 ;
у=0:
;
у=0:
 .
Если рассечь гиперболоид z=h,
то получим:
.
Если рассечь гиперболоид z=h,
то получим:
 . Из сказанного выше получаем, что
однополостный гиперболоид – неограниченная
поверхность и имеет вид:
. Из сказанного выше получаем, что
однополостный гиперболоид – неограниченная
поверхность и имеет вид:
двуполостный
гиперболоид:
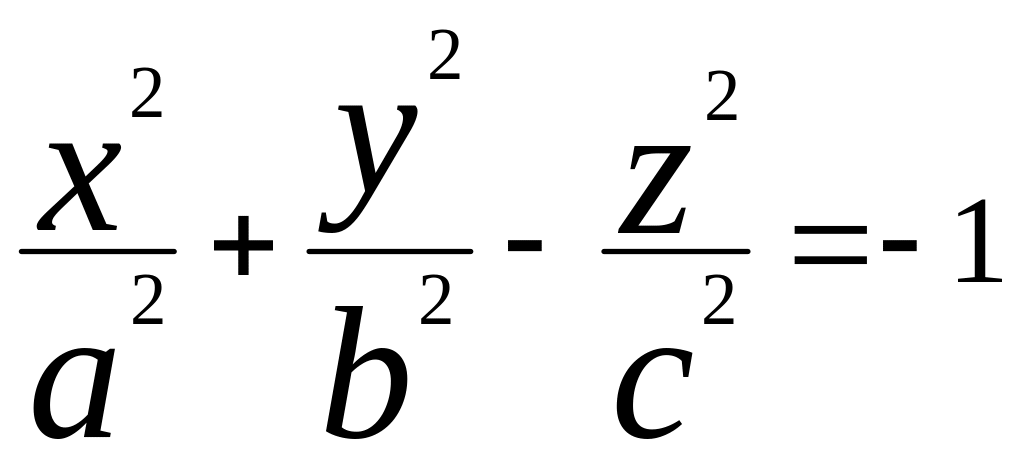 .
т. О(0;0;0)- центр симметрии; координатные
пл-ти явл. пл-ми симметрии; координатные
оси- осями симметрии. Если рассекать
эту поверхность пл-ми z=h
,
.
т. О(0;0;0)- центр симметрии; координатные
пл-ти явл. пл-ми симметрии; координатные
оси- осями симметрии. Если рассекать
эту поверхность пл-ми z=h
,![]() ,
то при
,
то при
![]() гиперболоид не будет иметь точек с
секущими пл-ми. При
гиперболоид не будет иметь точек с
секущими пл-ми. При
![]() двуполостный гиперболоид будет иметь
2 общие точки (0;0;с) и (0;0;-с). Если
двуполостный гиперболоид будет иметь
2 общие точки (0;0;с) и (0;0;-с). Если
![]() ,
то в сечении получим эллипс:
,
то в сечении получим эллипс:
 . Если мы рассечем поверхность пл-тью
х=0, то получим гиперболу:
. Если мы рассечем поверхность пл-тью
х=0, то получим гиперболу:

![]() ;
если у=0, то гиперболу:
;
если у=0, то гиперболу:
 .
Из сказанного выше двуполостный
гиперболоид неограниченная поверхность
и имеет вид:
.
Из сказанного выше двуполостный
гиперболоид неограниченная поверхность
и имеет вид:
эллиптический параболоид:
![]()

![]() х,у:
z
х,у:
z![]() 0.
Значит, что данная поверхность лежит в
полупространстве z
0.
Счение данной поверхности пл.-ми z=h>0
представляет собой эллипс:
0.
Значит, что данная поверхность лежит в
полупространстве z
0.
Счение данной поверхности пл.-ми z=h>0
представляет собой эллипс:
 .
А сечение поверхности координатными
плоскостями х=0 и у=0 будут явл. параболами.
Эти пл-ти явл. пл-ми симметрии,
.
А сечение поверхности координатными
плоскостями х=0 и у=0 будут явл. параболами.
Эти пл-ти явл. пл-ми симметрии,
а z- осью симметрии. Данная поверхность неограниченная и имеет вид:
гиперболический
параболоид:
 .
Сечение поверхности пл-тью у=0 или х=0
явл. параболой;
.
Сечение поверхности пл-тью у=0 или х=0
явл. параболой;
а![]() сечение параболоида пл-ми z=h
,
,
представляет собой гиперболы:
сечение параболоида пл-ми z=h
,
,
представляет собой гиперболы:
 . Ось z-
ось симметрии, а пл-ти х=0, у=0 – пл-ти
симметрии. Поверхность неограниченная.
. Ось z-
ось симметрии, а пл-ти х=0, у=0 – пл-ти
симметрии. Поверхность неограниченная.
к![]() онус:
.
т. О(0;0;0)- центр симметрии, оси и пл-ти –
оси и пл-ти симметрии. Сечение конуса
пл-ми х=0 (у=0) представляет собой пару
пересекающихся прямых, а сечение конуса
пл-тью z=h
представляет собой эллипс:
.
онус:
.
т. О(0;0;0)- центр симметрии, оси и пл-ти –
оси и пл-ти симметрии. Сечение конуса
пл-ми х=0 (у=0) представляет собой пару
пересекающихся прямых, а сечение конуса
пл-тью z=h
представляет собой эллипс:
.
Имеет следующий вид:
ц![]() илиндры:
а) эллиптический цилиндр
илиндры:
а) эллиптический цилиндр

![]() б)
гиперболический цилиндр
б)
гиперболический цилиндр

![]() в)
параболический цилиндр у2=2рх
в)
параболический цилиндр у2=2рх
30. Квадратичные формы: ранг, канонический и нормальный виды, сигнатура. Способы сведения к каноническому виду.
Квадратичной формой х1,х2,…,хn называют функцию f=a11x12+a12x1x2+…+a1nx1xn+a21x2x1+a22x22+…+a2nx2xn+…+annxn2, (1.1)
где коэффициенты aik, k,i=1…n –R или K числа. Далее будем считать, что aik=аki.
Если все коэффициенты квадратичной формы R числа, то форма называется действительной. Если – K, то комплексной формой.
С
квадратичной формой (1.1) можно связать
квадратичную матрицу:
Ранг r матрицы называется рангом квадратичной матрицы. Если r=n, то квадратичная форма называется невырожденной. Квадратичную форму (1.1) можно записать в матричном виде:
f=х1(a11x1+a12x2+…+a1nxn)+х2(a21x2+a22x2+…+a2nxn)+…=(
x1,
x2,..,
xn)*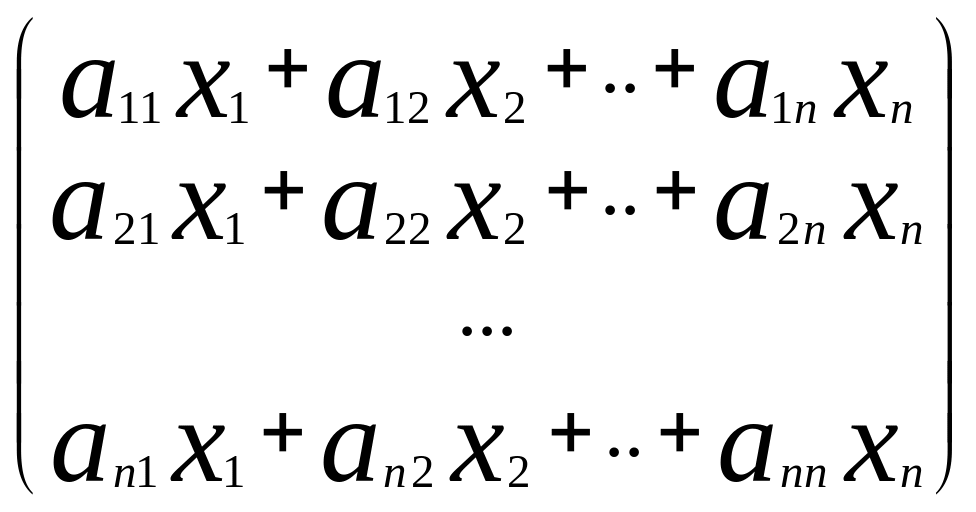 =( x1,
x2,..,
xn)*A*
=( x1,
x2,..,
xn)*A*![]()
Лемма. Если А и Q квадратичные матрицы порядка n. Причем, если Q – невырожденная матрица, то rank(Q*A)=rank(A*Q)=rankA.
![]()
 :
Известно,
что
rank(Q*A)
:
Известно,
что
rank(Q*A)![]() rankA и
что
rank(Q*A)
rankQ+
rankA-n. (т.к.
Q невырожденная
матрица,
то
rankQ=n) Следовательно
rank(Q*A)
rankA
rank(Q*A)= rankA.
rankA и
что
rank(Q*A)
rankQ+
rankA-n. (т.к.
Q невырожденная
матрица,
то
rankQ=n) Следовательно
rank(Q*A)
rankA
rank(Q*A)= rankA.
Преобразование матрицы квадратичной формы при линейной замене переменных.
Выполнив
в квадратичной форме (1.1) линейную замену
переменных:![]() (2.1)
(2.1)
через
Q-
матрицу линейного преобразования(2.1)
 выясним, какова матрица квадратичной
матрицы f
после замены. Для этого соотношение
(2.1) запишем в матричном виде X=Q*Y,
где
выясним, какова матрица квадратичной
матрицы f
после замены. Для этого соотношение
(2.1) запишем в матричном виде X=Q*Y,
где
 ,
,
 .
Сделаем замену переменных X=Q*Y;
f=Xt*A*X=(Q*Y)t*A*Q*Y=Yt*Qt*A*Q*Y=Yt*(Qt*A*Q)*Y.
Матрица В квадратичной формы f=Qt*A*Q.
Предположим, что (2.1) явл. невырожденной,
т.е. detQ
0.
Выясним, изменится ли rank
квадратичной формы при невырожденном
преобразовании переменных.
.
Сделаем замену переменных X=Q*Y;
f=Xt*A*X=(Q*Y)t*A*Q*Y=Yt*Qt*A*Q*Y=Yt*(Qt*A*Q)*Y.
Матрица В квадратичной формы f=Qt*A*Q.
Предположим, что (2.1) явл. невырожденной,
т.е. detQ
0.
Выясним, изменится ли rank
квадратичной формы при невырожденном
преобразовании переменных.
rankB=![]() Q
невырожденная матрица, то по лемме
Q
невырожденная матрица, то по лемме![]() =
rank((Qt*A)*Q)=
rank(Qt*A)=
rankA.
=
rank((Qt*A)*Q)=
rank(Qt*A)=
rankA.
Т.о. после невырожденного преобразования (2.1) rank квадратичной формы не меняется.
Каноническим
видом
квадратичной формы называется
![]() .
.
Теорема Число неравных нулю коэффициентов в каноническом виде квадратичной формы равно ее рангу.
Основная теорема о квадратичных формах.
квадратичная форма f=Xt*A*X может быть приведена к каноническому виду некоторым линейным невырожденным преобразованием переменных X=Q*Y. При этом, если квадратичная форма явл. R, то все элементы матрицы Q – R.(действительное линейное преобразование)
Алгоритм приведения квадратичной формы к каноническому виду методом Лагранжа.
пусть а11 в квадратичной форме (1.1) 0 полагаем
 ;
;
 и преобразуем квадратичную форму к
виду:
и преобразуем квадратичную форму к
виду:

если в квадратичной форме все аii=0,
 ,
то делают замену: а12
0.
,
то делают замену: а12
0.
x1=z1-z2
x2=z1+z2
xi=zi,
![]()
Закон инерции квадратичных форм.
Рассмотрим
R
квадратичные формы. Будем предполагать,
что переход от одной формы к другой
осуществляется лишь линейным
преобразованием переменных с R
коэффициентами. R
квадратичную форму f
ранга r
одним из таких преобразований переменных
можно привести к каноническому виду:
![]() .
Здесь коэффициенты b1,b2,..br
–R
0
числа, среди которых есть положит. и
отриц.
канонический вид
квадр.
формы f
действительного ранга r
можно записать:
.
Здесь коэффициенты b1,b2,..br
–R
0
числа, среди которых есть положит. и
отриц.
канонический вид
квадр.
формы f
действительного ранга r
можно записать:
![]() ,
где с1,с2,..сr>0.
Совершив невырожденное линейное
преобразование переменных, приведем
форму f
к нормальному
виду:
,
где с1,с2,..сr>0.
Совершив невырожденное линейное
преобразование переменных, приведем
форму f
к нормальному
виду:
![]() ,
,
![]() ,…,
,…,![]() .
.
![]()
Теорема (закон инерции R квадратичных форм)
Число положительных и отрицательных квадратов переменных в нормальном виде, к которому приводится квадратичная R форма c R невырожденным линейным преобразованием переменных, не зависит от выбора этого преобразования.
Обозначим
через
![]() число квадратов переменных с коэффициентом
(+1) в нормальном виде, к которому приводится
квадратичная форма f;
а через
число квадратов переменных с коэффициентом
(+1) в нормальном виде, к которому приводится
квадратичная форма f;
а через
![]() - с коэффициентом (-1).
- с коэффициентом (-1).
Величина называется положительным индексом инерции квадратичной формы, а величина - отрицательный индекс инерции. S= - -сигнатура квадратичной формы. Очевидно, что r= + , где r – rank кв.формы.
Заметим,
что если кв.форма приведена к кан.виду:
,
![]() .
Т.о. положит. индекс инерции равен числу
положительных коэффициентов при
квадратах переменных, а отриц.индекс –
число отрицательное.
.
Т.о. положит. индекс инерции равен числу
положительных коэффициентов при
квадратах переменных, а отриц.индекс –
число отрицательное.
Теорема.
Для того,
чтобы 2 R
кв.формы f
и g
от одинакового числа переменных могли
быть переведены одна в другую невырожденными
линейными преобразованиями переменных
![]() чтобы
они имели одинаковые ранги и сигнатуры.
чтобы
они имели одинаковые ранги и сигнатуры.
Кв.форма от n переменных называется положительно определенной, если она приводится к нормальному виду, состоящему из n положительных квадратов переменных. rank=n, =n, =0.
Теорема. Для того, чтобы R кв.форма f от n переменных явл. положительно определенной при R значениях переменных, среди которых хотя бы одно значение отличное от 0, кв.форма принимает положит. значение.
Лемма.
Пусть
![]() -det
матрицы R
кв.формы
-det
матрицы R
кв.формы
![]() .Пусть
X=Q*Y
-
невырожденное
R
преобразование переменных. Тогда det
матрицы кв.формы сохраняет знак при
преобразовании X=Q*Y.
.Пусть
X=Q*Y
-
невырожденное
R
преобразование переменных. Тогда det
матрицы кв.формы сохраняет знак при
преобразовании X=Q*Y.
: f=Xt*A*X; X=Q*Y; f=(Q*Y)t*A*(Q*Y)=Yt*(Qt*A*Q)*Y; B= Qt*A*Q

![]() -
знаки
совпадают.
-
знаки
совпадают.
Теорема.(критерий
Сильвестра) Для
того, чтобы кв.форма f=Xt*A*X
от n
переменных была положительно
определенной
чтобы
все главные миноры ее матрицы А были
строго положительны, т.е. а11>0;
 >0,…
>0,…
Приведение кв.формы к кан.виду ортогональными преобразованиями переменных.
(6.1)
называется ортогональным, если матрица Q этого преобразования явл. ортогональной, т.е. Q-1=Qt. Рассмотрим R кв.форму от n переменных f=Xt*A*X.
Пусть
V
-
n-мерное
евклидово пространство над полем R
чисел. Возьмем
ортонормированный базис (![]() )
V
и будем смотреть на матрицу А, как на
матрицу линейного оператора
)
V
и будем смотреть на матрицу А, как на
матрицу линейного оператора
![]() .
Т.к. матрица А симметрична и все ее эл-ты
R
числа, то рассматриваемый линейный
оператор
.
Т.к. матрица А симметрична и все ее эл-ты
R
числа, то рассматриваемый линейный
оператор
![]() явл.
самосопряженным. Известно, что
самосопряженный оператор
порождает
в V
ортонормир. базис (f1,f2,..,fn),
все векторы кот. явл. собственными
векторами оператора
.
Матрица оператора
в
базисе (f1,f2,..,fn),
явл.
самосопряженным. Известно, что
самосопряженный оператор
порождает
в V
ортонормир. базис (f1,f2,..,fn),
все векторы кот. явл. собственными
векторами оператора
.
Матрица оператора
в
базисе (f1,f2,..,fn),![]() явл. диагональной:
явл. диагональной: , где
, где
![]() -
собственные значения оператора
.
Матрица А связана с
соотношением В=Q-1*A*Q,
где Q-матрица
перехода от базиса (
)
к базису (f1,f2,..,fn).
-
собственные значения оператора
.
Матрица А связана с
соотношением В=Q-1*A*Q,
где Q-матрица
перехода от базиса (
)
к базису (f1,f2,..,fn).
![]()
Известно, что матрица перехода от одного ортонормированного базиса к другому пр-ва V явл. ортогональной. Q- ортогональная матрица.
B= Qt*A*Q (6.2)
Известно, что при замене переменных (6.1) матрица А рассматриваемой кв.формы f преобразуется в матрицу В по закону (6.2). Т.о., если в (6.1) в качестве Q взять ортогональную матрицу перехода, то В кв.формы f после замены переменных (6.1) будет диагональной, а форма примет кан. вид:
![]()
Алгоритм приведения кв.формы к кан.виду операторным преобразовнием переменных.
записать матрицу А в кв.форме
определить из ур-я
 собственные значения матрицы А
собственные значения матрицы Асобственного значения
 определить соответствующие ему линейно
независимые собственные векторы(n-мерные
матрицы столбцы); координаты этих
векторов удовлетворяют следующей
однородной системе ур-ий:
определить соответствующие ему линейно
независимые собственные векторы(n-мерные
матрицы столбцы); координаты этих
векторов удовлетворяют следующей
однородной системе ур-ий:
 .
Искомая совокупность линейно независимых
собственных векторов образует ФСР этой
системы ур-ий.
.
Искомая совокупность линейно независимых
собственных векторов образует ФСР этой
системы ур-ий.Полученным собственным векторам, отвечающим собственному значению применить процесс ортогонализации
после того, как будут найдены все n собственных векторов n, образующим базис (f1,f2,..,fn) в n-мерном Rевклидовом пр-ве матрицу столбцов нужно координаты векторов
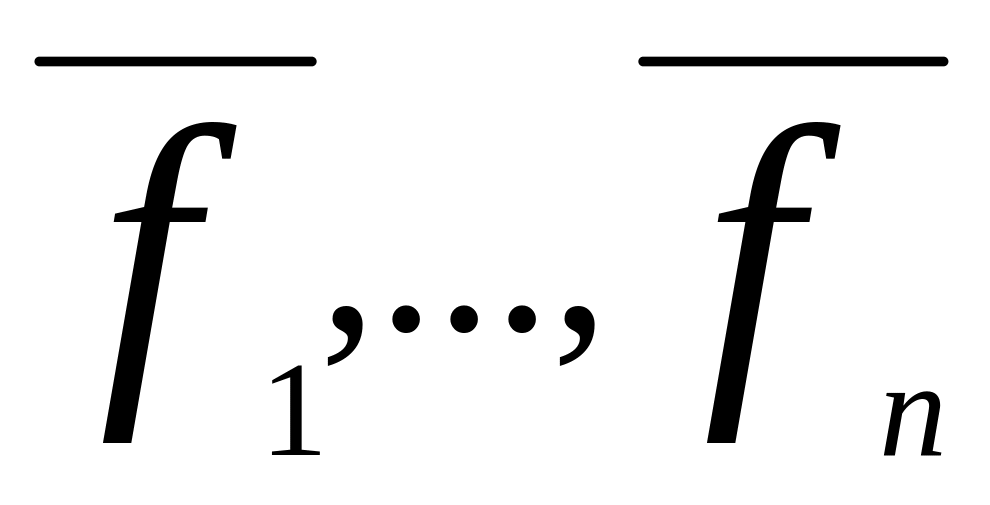 поместить в соответствующие столбцы
искомой матрицы Q.
поместить в соответствующие столбцы
искомой матрицы Q.Написать кан. вид кв.формы: ; записать вид линейного преобразования переменных
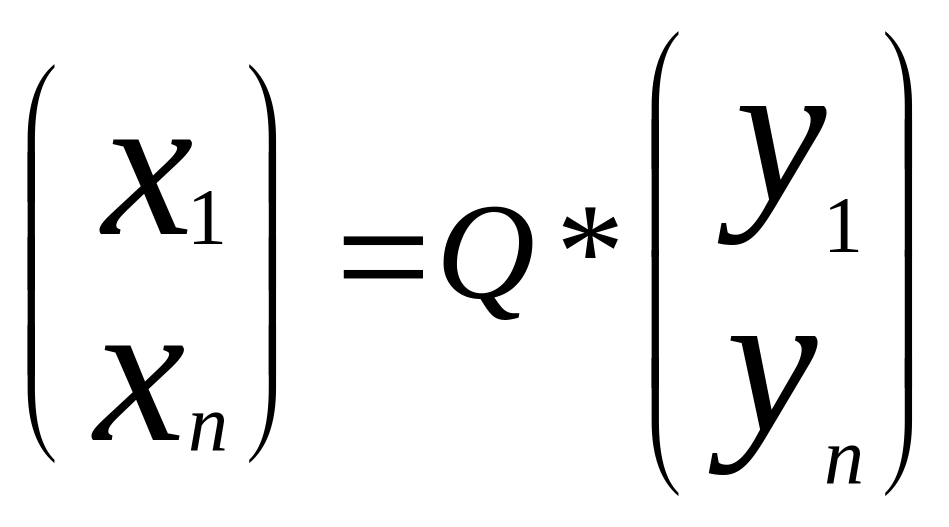
Лемма. Нормальный вид положительно-определенной кв.формы сохраняется при ортогональном преобразовании переменных
Теорема. 2 R кв.формы f и g от n переменных x1,x2,…,xn можно привести к кан.виду при помощи одного R линейного преобразования переменных, если одна из форм явл. положительно определенной.
