6). Если сравнение имеет место по модулю m, то оно имеет место и по любому

делителю числа m. 7). Общий делитель одной части сравнения и модуль является делителем другой части сравнения: , .

Малая теорема Ферма: если a и m – взаимнопростые числа, тогда . Функция Эйлера – это число положительных чисел, не превосходящие n и взаимнопростые с n. Если целое число a взаимнопростое с m, то . Теорема Эйлера: если целое число a взаимнопростое с m, то . Теорема Ферма: 1. Если целое число a не делит p, где р – простое, то . 2. Если р – простое и а –любое целое число, тогда . Отношение сравнимости – это классы эквивалентности. Классы эквивалентности также называются классами вычетов, а их эквивалентности называют вычетами.

Решение сравнений: Пусть , , mєN. Тогда называется сравнением к – степени с одним неизвестным и имеет не более, чем m классов решений. Решениями данного сравнения будут являться классы вычетов по модулю m. Сравнения первой степени с одной неизвестной можно записать в виде: если: 1). это сравнение не имеет решения (например 5x ). 2). Если решение этого сравнения. 3). . Теорема: Пусть , , то , d – класов решений mod m. Методы решения сравнений: 1). Метод испытания полной системы вычетов. 2). Метод преобразования коэффициентов. Прибавляется или вычитается из правой части любое число, кратное модулю, заменяя коэффициенты в левой части на число сравнений с модулем. Можно преобразовать сравнения так, что его можно будет сократить на а и получить решение.

Пример: 5x . 3). Решение сравнений с помощью системы Эйлера: . Тогда . . (5х

=> ).

42. Поверхности вращения 2- го порядка.

К поверхностям вращения второго порядка относятся: эллипсоид, однополосный гиперболоид, двуполостный гиперболоид, эллиптический параболоид, гиперболический параболоид и конус второго порядка.

Эллипсоид: Исследуем поверхность, заданную уравнением: . Рассмотрим сечения этой поверхности с плоскостями, параллельными плоскости xOy. Уравнения таких плоскостей: z=h, где h – любое число. Линия, получаемая в сечении, определяется двумя уравнениями: . Исследуем эти уравнения: а) Если . Точек поверхности пересечения поверхности с плоскостями z=h – не существует. б) Если . Линия пересечения вырождается в две точки: (0;0;с) и (0;0;-с). Плоскости z=c и z=-c касаются данной поверхности. в) если то уравнения можно переписать в виде: 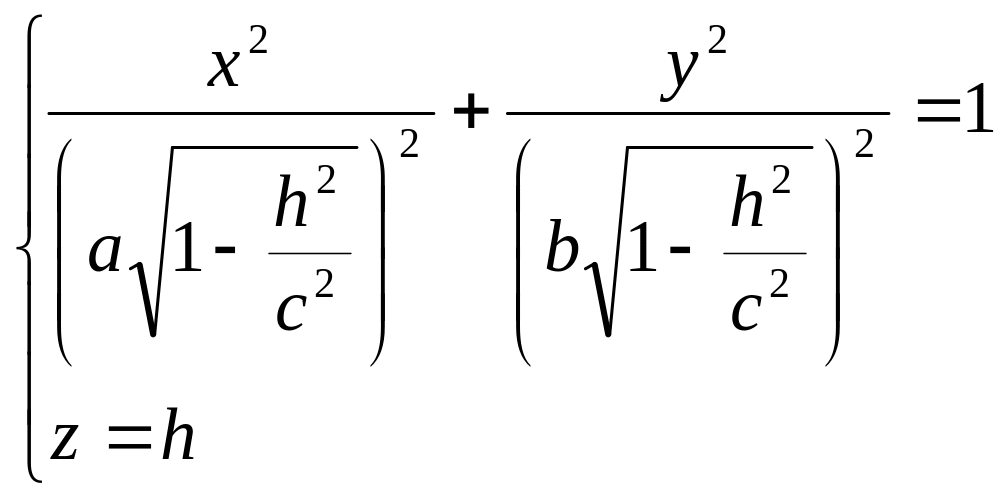. Как видно, линия пересечения есть эллипс с полуосями (рис):

и . При этом чем меньше , тем

больше полуоси а₁ и в₁. При h=0 они достигают своих

наибольших значений: а₁=а, в₁=в. Уравнения

примут вид: . Аналогичные

результаты получим, если рассмотрим сечения поверхности плоскостями x=h и y=h. Таким образом, рассмотренные сечения позволяют изобразить поверхность как замкнуто овальную поверхность. Эта поверхность называется эллипсоидом. Величины а, в и с называются полуосями эллипсоида. Если все они различны, то эллипсоид называется трехосным. Если какие-либо две полуоси равны, трехосный эллипсоид превращается в эллипсоид вращения. Если а=в=с, то он превращается в сферу: .

Однополосный гиперболоид: Исследуем поверхность, заданную уравнением: . Пересекая эту поверхность плоскостью z=h, получим линию пересечения, уравнения которой имеют вид: или 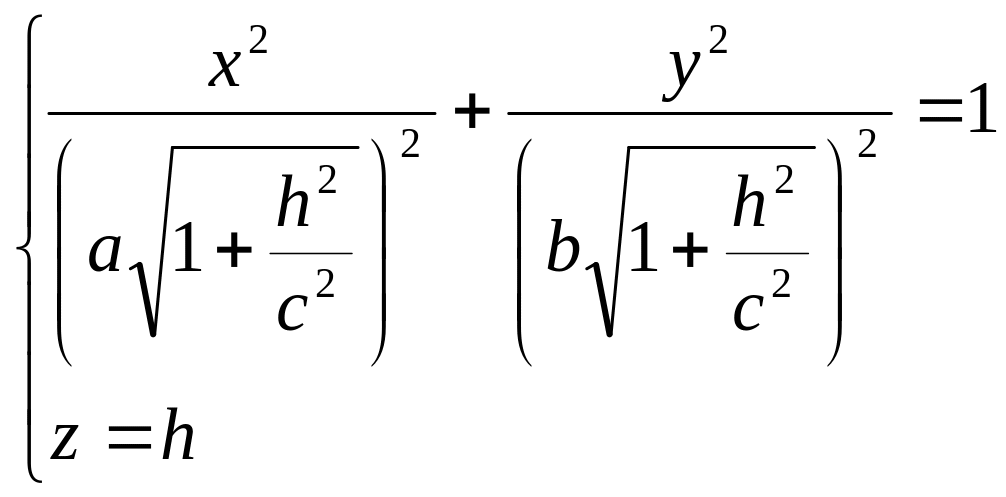. Как видно, этой линией является эллипс с полуосями: и . Полуоси а₁ и в₁ достигают своего наименьшего значения

при h=0: а₁=а, в₁=в. При возрастании полуоси эллипса

будут увеличиваться. Если пересекать поверхность

плоскостями x=h или y=h, то в сечении

получим гиперболы. Найдем, например, линию

пересечения поверхности с плоскостью Оxy,

уравнение которой x=0. Эта линия пересечения описывается

уравнениями: . Как видно, эта линия есть гипербола. Поверхность называется однополосным гиперболоидом.

Двуполостный гиперболоид: Пусть поверхность задана уравнением:

. Если эту поверхность пересечь плоскостями z=h, то линия пересечения определяется уравнениями: . Отсюда следует, что: а) если то плоскости не пересекают поверхности. б) если то плоскости касаются данной поверхности соответственно в точках (0;0;с) и (0;0;-с). в) если , то уравнения могут быть переписаны так:

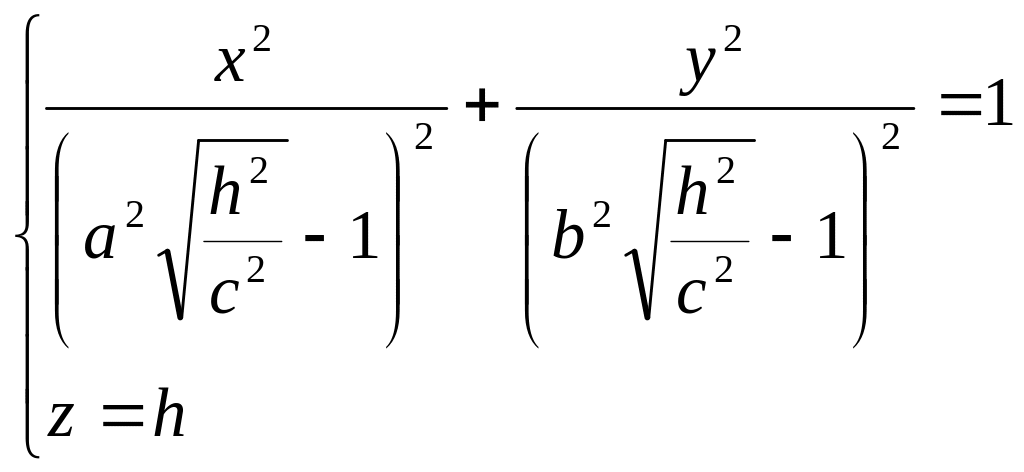. Эти уравнения

определяют эллипс. Пересекая поверхность

координатными плоскостями Oxy

(x=0), Oxy(y=0), получим в сечении гиперболы уравнения которых имеют вид: и . У обеих гипербол действительной осью является ось Oz. Поверхность называется двухполостным гиперболоидом.

Эллиптический параболоид: Исследуем поверхность, заданную уравнением:

, где р>0, q>0. Рассечем эту поверхность

плоскостями z=h. В сечении получим линию, уравнения

которой есть: . Если h<0 то плоскости z=h

поверхности не пересекают. Если h>0, то в сечении

имеем элипс, уравнение которого имеет вид: . Его полуоси возрастают с ростом h. При пересечении поверхности координатными плоскостями Oxz и Oyz получатся соответственно параболы: и . Таким образом, поверхность, определяемая уравнением , имеет вид выпуклой, бесконечно расширяющейся чаши. Эта поверхность называется эллиптическим параболоидом.

Гиперболический параболоид: Исследуем поверхность, определяемую уравнением: , где р>0, q>0. Рассечем эту поверхность плоскостями z=h. Получим кривую: , которая при всех значениях является гиперболой. При h>0 ее действительные оси паралельны оси Ох. При h<0 – паралельны оси О. При h=0 линия пересечения распадается на пару пересекающихся прямых и . При пересечении поверхности плоскостями, параллельными плоскости Oxz (y=h), будут получатся параболы: ,

ветви которых направлены вверх. При у=0 в сечении

получается парабола: с вершиной в начале

координат и осью симметрии Oz. Пересекая

поверхность плоскостями x=h, получим параболы: , ветви которых направлены вниз. Эта поверхность имеет вид седла. Поверхность называется гиперболическим параболоидом.