47. Матрицы. Операции над матрицами. Ранг матрицы.

Матрицей называется прямоугольная таблица специального вида.

Обозначается большими латинскими буквами. Если в матрице m строк и n столбцов, то говорят, что матрица имеет размеры mxn. Элементы матриц обозначают соответствующие малые буквы с двумя нижними индексами: первый – номер строки, второй – столбца: a₁₂=3, a₂₃=6.

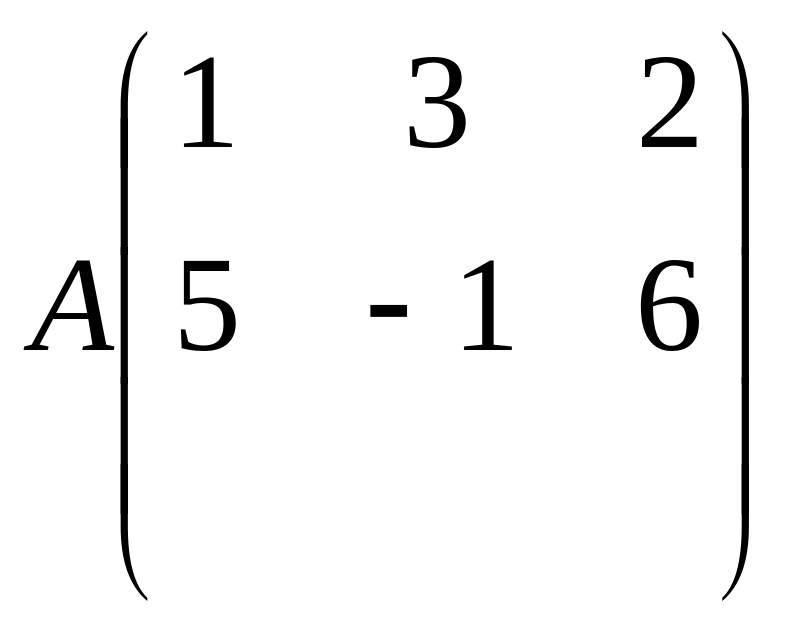
Если количество строк и количество столбцов в матрице одинаково, то такая матрица называется квадратной, а число строк – ее порядком. Например:

- квадратная матрица двойного порядка.

Матрица, состоящая из одной строки (столбца) называется вектором-строкой, (вектором-столбцом). Матрица называется нулевой, если все ее элементы равны нулю. Главной (побочной) диагональю квадратной матрицы называется диагональ, проведенная из левого верхнего угла в правый нижний (из правого верхнего угла в левый нижний). Квадратная матрица называется единичной, если по ее главной диагонали стоят единицы, а все остальные элементы =0. Квадратная матрица называется диагональной, если все элементы вне главной диагонали =0. Квадратная матрица называется скалярной, если все элементы вне главной диагонали =0, а все элементы главной диагонали = между собой. Квадратная матрица называется верхнетриугольной (нижнетриугольной), если все элементы, находящиеся ниже (выше) главной диагонали =0. Матрица, которая является и верхнетриугольной и нижнетриугольной будет диагональной.

Операции над матрицами:

Две матрицы называются равными, если они имеют одинаковые размеры и их соответствующие элементы равны.

1. Умножение матрицы на число:

Умножать на число можно матрицу любого размера. При этом получая матрицу такого же размера. Все элементы исходящей матрицы умножаем на данное число.

2. Сложение матриц:

Складывать можно матрицы одинакового размера. В результате получается матрица такого же размера. Матрицы складываются покомпонентно:

А_mxn+B_mxn=C_mxn

3. Линейные операции:

1. Асоциативность: (А+В)+С=А+(В+С)

2. Свойство существования нейтрального элемента: А+ =В+ =А

3. Существование противоположного элемента: А+(-А)= .

4. Комутативность: А+В=В+А.

5. 1*А=А. 7.

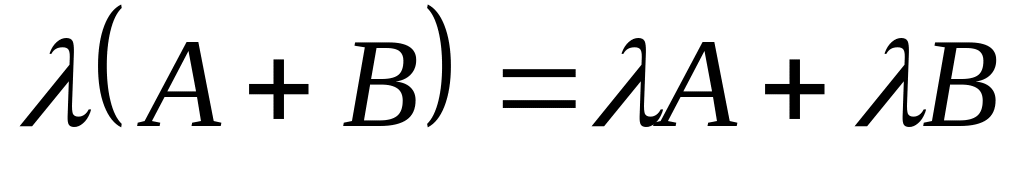
6. Дистрибутивность: 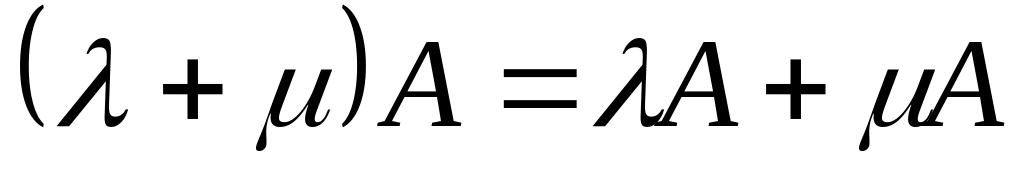. 8.

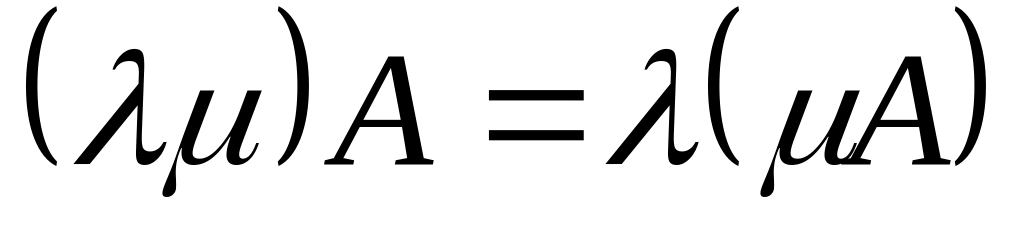
4. Умножение матриц:

Умножать матрицу А на матрицу В можно только тогда, когда количество столбцов матрицы А = количеству строк матрицы В. Произведение матрицы А и В называется матрица С, такая, что для любого i, j, элементы матрицы С_ij = произведению i-ой строки матрицы А на j-ый столбец матрицы В: А_mxnB_nxk=C_mxk.

5. Обратная матрица:

На множестве матриц нет операции деления. Частично эту операцию можно заменить на умножение на обратную матрицу. Квадратная матрица В называется обратной к квадратной матрице А, если АхВ=ВхА=Е. В=А^-1.

А= А^-1= А*А^-1=

Если к матрице существует обратная, то она единственная. Вычислить обратную матрицу можно еще и с помощью формулы: А^-1= (с помощью союзной).

Ранг матрицы:

Рангом матрицы называется ранг ее системы строк (или столбцов): А= 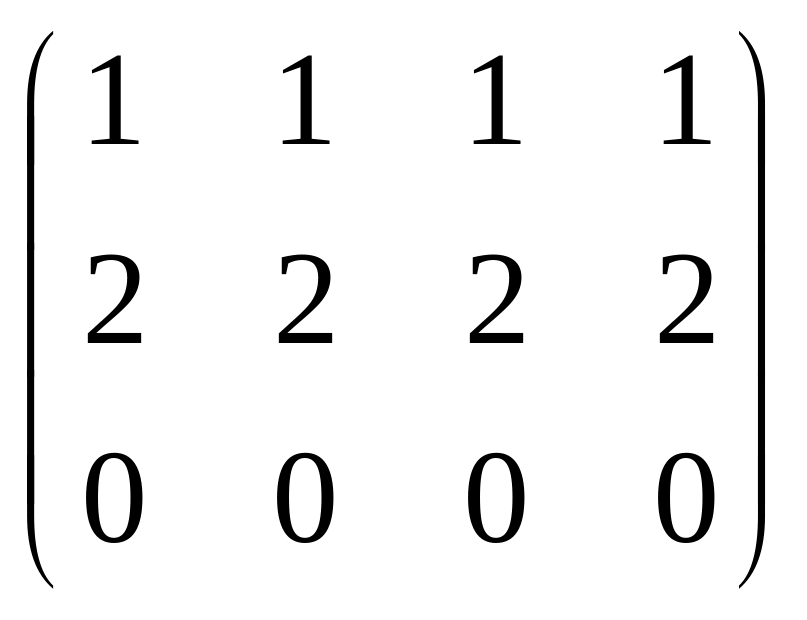rang А=1.

Теорема: Для любой матрицы строчный ранг = ее столбцовому рангу.

Две системы строк называются эквивалентными, если каждая из строк первой системы есть линейная комбинация второй системы и наоборот. Ранги эквивалентных систем строк равны. При эквивалентных преобразованиях над строками матрицы ее ранг не изменяется. Ранг матрицы равен количеству не нулевых строк после приведения ее к ступенчатому виду с помощью элементарного преобразования.

59. Гомоморфизм групп.

Множество g называется группой, если на этом множестве задана одна алгебраическая операция (сложения или умножения) и выполняются:

1. Замкнутость относительно введенной операции : для любых а и в є g: а*в є g.

2. Ассоциативность: для любых а, в, с є g: (а*в)*с=а*(в*с).

3. Существование единственного нейтрального элемента: существует e є g такое, что для любого а є g, а*е=е*а=а.

4. Существование обратного элемента: для любого а є g существует единственные элемент а^-1 , такой, что а*а^-1=а^-1*а=е.

Пусть H є G, тогда H будет называться подгруппой, если оно само образует группу относительно операций, введенных на группе G. Пусть g₁ и g₂ группы. Отображение называется гомоморфизмом, если для любого g₁ , h є g₁: , где * - операция из g₁, - операция из g₂. Гомоморфизм – это такое отображение, которое сохраняет операцию.

Свойства гомоморфизма: Пусть , тогда:

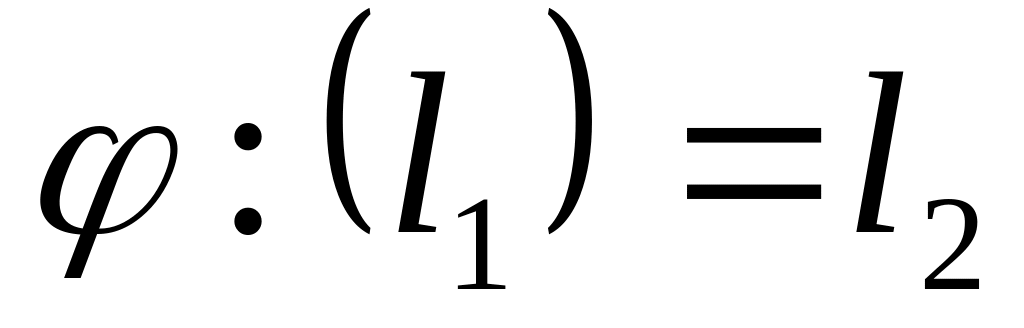1. , где l₁ – нейтральный элемент группы g₁, l₂ –группы g₂.

2. Для любого g є g_1:

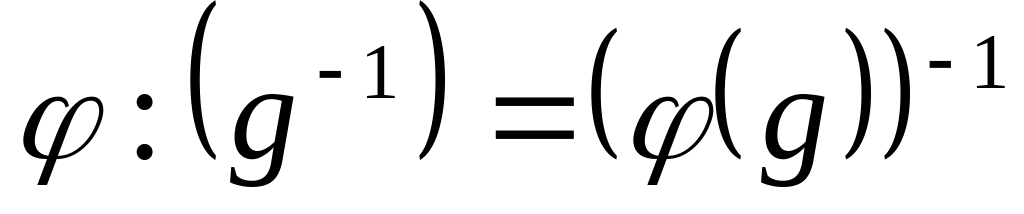
Ядром (ker ) гомоморфизма называется множество . Образом гомоморфизма называется множество: . Ядро гомоморфизма является подгруппой g₁, а образ – подгруппой группы g₂. Гомоморфизм является изоморфизмом тогда и т. т., к. его ядро тривиально, а образ совпадает с g₂: .

60. Высказывания и операции над ними. Таблицы истинности.

Высказывание –это повествовательное предложение о котором можно сказать, что оно истинно или ложно (2*3=5 –ложное). Высказывания могут являться истинными или ложными.

Логические операции над высказываниями:

1. Отрицание – высказывание А, высказывание не А которое истинно тогда

и только тогда, когда А – ложное.

2. Коньюнкция ( 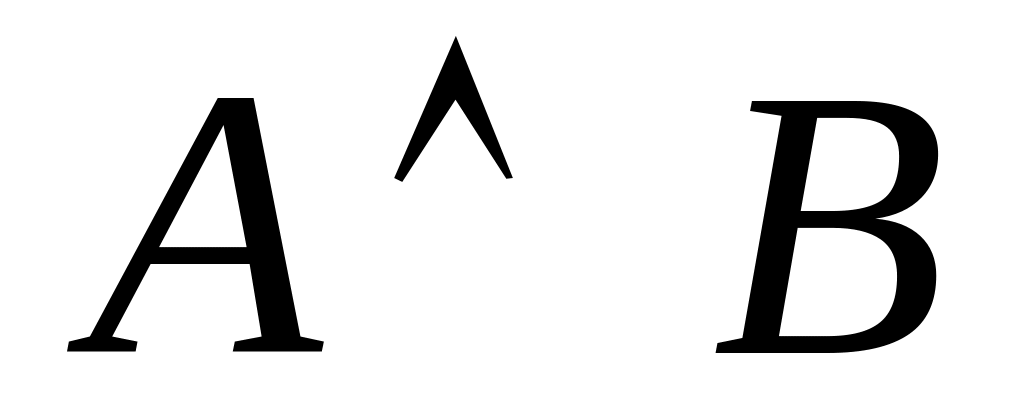)– высказывание А и В, которое истинно тогда и только

тогда, когда А – истинно и В – истинно.

3. Дезьюнкция (АvВ (А или В)) – высказывание А и В которое ложно , если А

и В – ложны.

4. Импликация (А => B) – высказывание А и В, которое будет ложно т. и т. т.,

к. А –истино и В – ложно.

5. Эквиваленция (АB)– высказывание А и В, которое истино т. и т. т., к. А=В.

Теперь построим таблицу истинности для данных высказываний:

А	В			АvВ	А => B	АB
0	0	1	0	0	1	1
0	1	1	0	1	1	0
1	0	0	0	1	0	0
1	1	0	1	1	1	1

Формула логики высказываний называется тавтологией, если она истина при

любых значениях, входящих в нее элементарных высказываний. Например:

А		Аv
0	1	1
1	0	1

Формула логики высказываний называется тождественно ложной ( ), если она ложна при любых значениях, входящих в нее элементарных высказываний. Формула В (А₁,…,А_n В) называется логически выводимой из А₁,…,А_n , если при любом выборе элементарных высказываний, входящих в состав формулы А₁,…,А_n формула В будет истина всякий раз, когда будет истина вся формула А₁,…,А_n. Формулы А и В называются равносильными или логически эквивалентными, если они принимают одинаковые значения при любом выборе элементарных высказываний (т.е. если их таблицы истинности совпадают).

Законы Де – Моргана: 1) ; 2) .

Теорема: - тавтология.

Можно привести такие наиболее встречающиеся формулы логических высказываний:

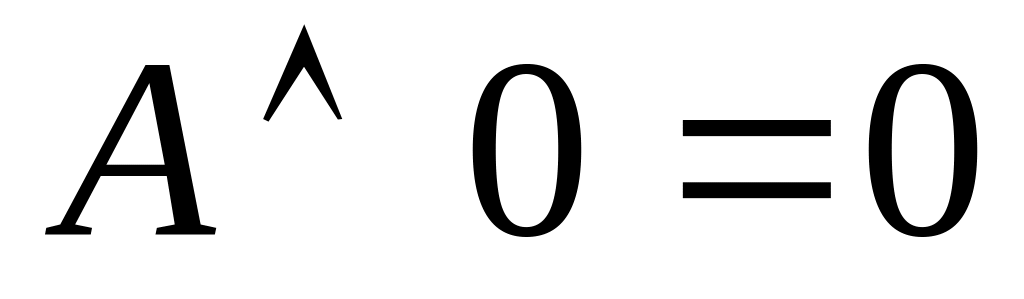
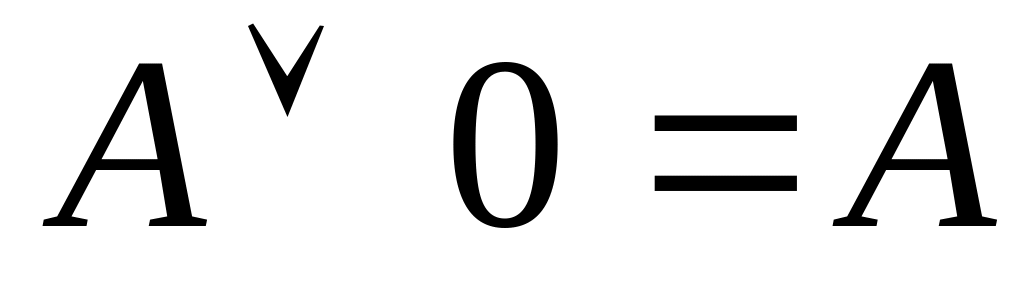1. 5) 9) (А*В)*С=А*(В*С

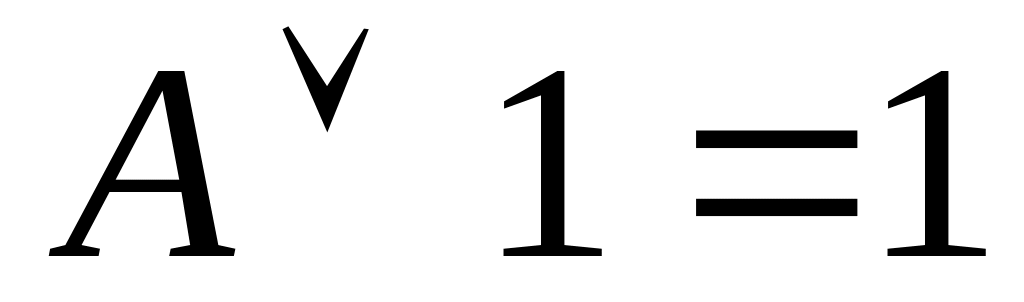2. 6) 10) (АvВ) С=АСvВС

3. 7) 11)

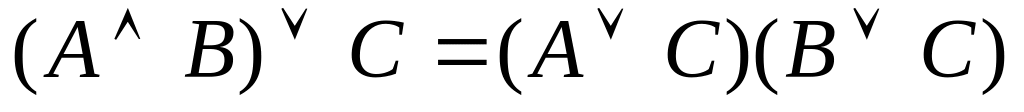
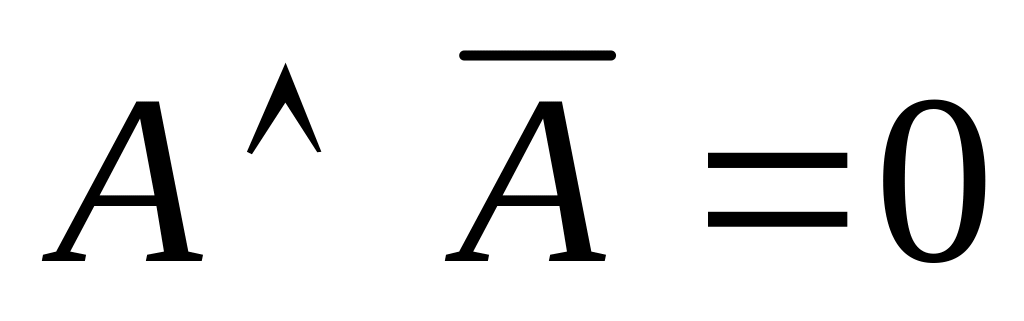
4. 8) А*В=В*А 12) АvАВ=А

13) А=>В=

14) АВ=(А=>B)(B=>A) 17) AB=

15) AB= ) 18) A

16) AB=AB 19)

43. Репер Френе кривой. Формулы Френе. Кривизна и кручение кривой.

Пусть , - кривая класса Сⁿ, n . Репером Френе этой кривой в т. М₀₌ , называется правый ортонормированный репер , - векторы базисных репера, базисные вектора, которые определяют соответственно касательную кривую, главную нормаль и бинормаль в т. М₀. Формулы по касательным: . Допустимая замена параметра: . Бинормалью кривой в т. М₀ называется прямая, перпендикулярная соприкасанию плоскости в т. М₀. Нормалью кривой в т. М₀ называется пересечение нормальной и соприкасающей плоскости в т. М₀. Соприкасающей плоскостью кривой в т. М₀ называется положение секущей плоскости при условии, что т. М₁ и т. М₂ стремится по кривой к т. М₀, т. е. , .

Формулы Френе: Пусть , s – длина дуги. Кривая класса - произвольная точка, . Тогда формулы Френе кривой имеют вид: , где ,

- скалярные функции.

Кривизна кривой: Пусть , , называется вектором кривизны кривой, а его модуль - кривизной кривой, т. к. , т. е. можно сказать, что кривизна кривой – это коэффициент к в формулах Френе. Теорема: Кривизна кривой в т. М₀ равна угловой скорости вращения касательной кривой в этой точке: , где - приращение угла между касательными на дуге кривой. Если в т. М₀ кривой , то число называется радиусом кривизны кривой. Для того, чтобы кривая была прямой или ее частью нужно, чтобы в каждой точке этой кривой кривизна =0. Точка кривой, в которой к=0 называется точкой распределения. Кривизна вычисляется по формуле:

или .

Кручение: Кручением кривой в данной точке М=r называется коэфициент . В формулах Френе этой кривой, записанных для значения параметра s₀. Теорема (критерий плоской кривой):кривая является плоской т. и т. т., к. в каждой точке кручение =0. Точка кривой, в которой кручение =0 называется точкой уплощения. Абсолютным кручением кривой называется модуль вектора : . . Кручение показывает на отличие пространственной кривой от плоской кривой. Кручение можно вычислить по формулам: или .