
44. Первая квадратическая форма поверхности. Понятие внутренней геометрии поверхности.
Первой квадратической формой поверхности s называется квадратическая форма:
![]() ,
где
,
где
![]() - коэффициенты первой квадр. формы. Для
поверхности, заданной явным уравнением
- коэффициенты первой квадр. формы. Для
поверхности, заданной явным уравнением
![]() коэфоциенты I квадратической формы
имеют вид:
коэфоциенты I квадратической формы
имеют вид:
![]() .
I
квадратическая форма есть позитивно
определенной. Для коэффициентов I кв.
формы используются такие обозначения:
.
I
квадратическая форма есть позитивно
определенной. Для коэффициентов I кв.
формы используются такие обозначения:
![]()
![]() .
Матрица
.
Матрица
![]() называется матрицей I кв. формы.
Определитель этой матрицы будем
обозначать символом g. Матрица, обратная
к данной записывается в виде:
называется матрицей I кв. формы.
Определитель этой матрицы будем
обозначать символом g. Матрица, обратная
к данной записывается в виде:
![]() и ее элементы выражаются через элементы
матриц I кв. формы по таким формулам:
и ее элементы выражаются через элементы
матриц I кв. формы по таким формулам:
![]() ,
,
![]() .
.
Геометрический
смысл: На поверхности зададим кривую:
![]() .
Найдем длину дуги S:
.
Найдем длину дуги S:
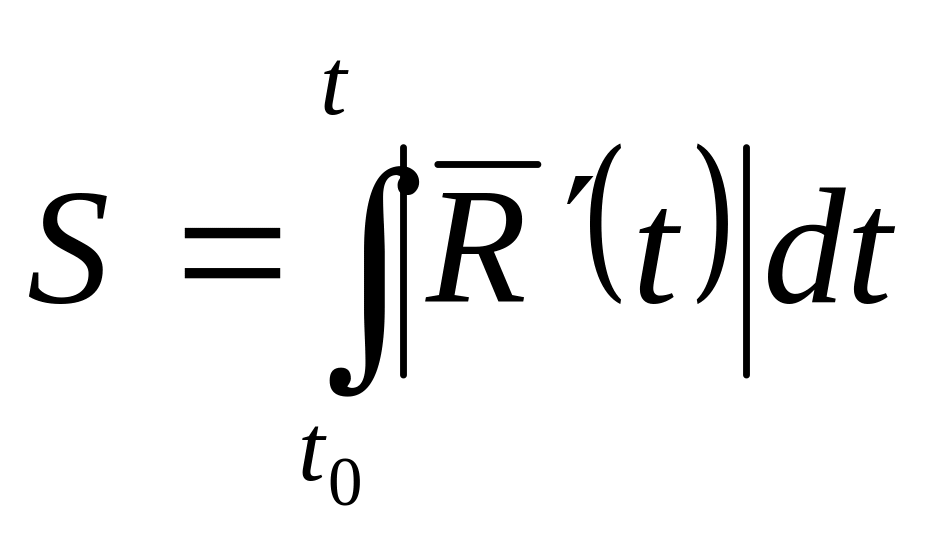 -
длина дуги.
-
длина дуги.
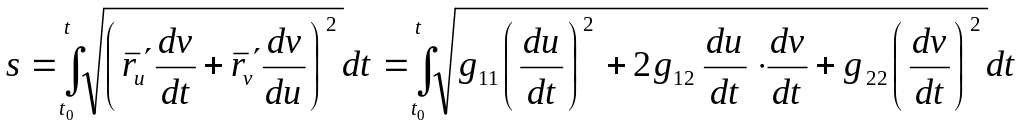 - длина этой кривой. перейдем к
дифференциалу:
- длина этой кривой. перейдем к
дифференциалу:
![]() - дифференциал длины дуги.
- дифференциал длины дуги.
![]() или
или
![]() .
Первая квадратическая форма поверхности
= квадрату дифференциала длины дуги =
метрической форме.
.
Первая квадратическая форма поверхности
= квадрату дифференциала длины дуги =
метрической форме.
Длина
дуги кривой на поверхности: Пусть
![]() - поверхность,
- поверхность,
![]() - кривая, лежащая на ней, Р0
– точка, общая для Ф и
,
r=r(u,v)
– какая-нибудь параметрическая
поверхность, в окрестности т. Р0.
Каждой
т. Р(t) соответствует значение: u(t),
v(t)
такие, что
- кривая, лежащая на ней, Р0
– точка, общая для Ф и
,
r=r(u,v)
– какая-нибудь параметрическая
поверхность, в окрестности т. Р0.
Каждой
т. Р(t) соответствует значение: u(t),
v(t)
такие, что
![]() .
Равенства u=u(t), v=v(t) мы будем называть
уравнением кривой на поверхности. Пусть
Ф –регулярная поверхность,
-
регулярная кривая на ней. Пусть r=r(u,v)
и
r=r(t)
их
регулярные параметры в окрестности т.
Р0,
удовлетворяющие обычным условиям:
vu
.
Равенства u=u(t), v=v(t) мы будем называть
уравнением кривой на поверхности. Пусть
Ф –регулярная поверхность,
-
регулярная кривая на ней. Пусть r=r(u,v)
и
r=r(t)
их
регулярные параметры в окрестности т.
Р0,
удовлетворяющие обычным условиям:
vu![]() rv
rv![]() ,
,
![]() ,
тогда в уравнениях кривой на поверхности
u=u(t), v=v(t) функции u(t) и v(t) регулярные
функции, причем
,
тогда в уравнениях кривой на поверхности
u=u(t), v=v(t) функции u(t) и v(t) регулярные
функции, причем
![]() .
Кривую поверхности всегда можно задать
в окрестности каждой точки равенствами
u=u(t), v=v(t), причем если поверхность и
кривая - регулярны, то и u(t) и v(t) –
регулярные функции. Рассмотрим длину
дуги на поверхности. Пусть Ф –регулярная
поверхность, и r=r(u,v)
–
ее регулярные параметры. Пусть
- регулярная кривая на поверхности,
заданная уравнениями: u=u(t), v=v(t). Найдем
выражение длины дуги отрезка кривой с
концами в т. Р0(t0)
и Р(t).
Имеем:
.
Кривую поверхности всегда можно задать
в окрестности каждой точки равенствами
u=u(t), v=v(t), причем если поверхность и
кривая - регулярны, то и u(t) и v(t) –
регулярные функции. Рассмотрим длину
дуги на поверхности. Пусть Ф –регулярная
поверхность, и r=r(u,v)
–
ее регулярные параметры. Пусть
- регулярная кривая на поверхности,
заданная уравнениями: u=u(t), v=v(t). Найдем
выражение длины дуги отрезка кривой с
концами в т. Р0(t0)
и Р(t).
Имеем:
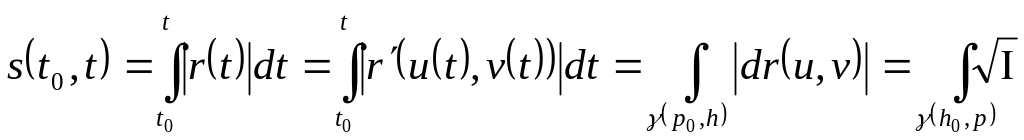 -квадратическая форма поверхности. Для
измерения дуги кривой на поверхности
достаточно знать I кв. форму поверхности.
I
кв. Форма задает матрицу поверхности,
и часто называет ее линейным элементом
поверхности. I
кв. форма
не
определяет поверхность однозначно.
-квадратическая форма поверхности. Для
измерения дуги кривой на поверхности
достаточно знать I кв. форму поверхности.
I
кв. Форма задает матрицу поверхности,
и часто называет ее линейным элементом
поверхности. I
кв. форма
не
определяет поверхность однозначно.
45. Вторая квадратическая форма поверхности. Ее геометрический смысл и применение.
II
квадратической формой поверхности
называется квадратическая форма,
определенная в т. М и ассоциированная
с оператором Вейерштрасса в этой точке.
II
квадратическую форму можно подать в
виде формулы:
![]() ,
где
,
где
![]() ,
,
![]() ,
,
![]() - коэффициенты II квадратической формы.
Если поверхность задана уравнением
- коэффициенты II квадратической формы.
Если поверхность задана уравнением
![]() ,
то
,
то
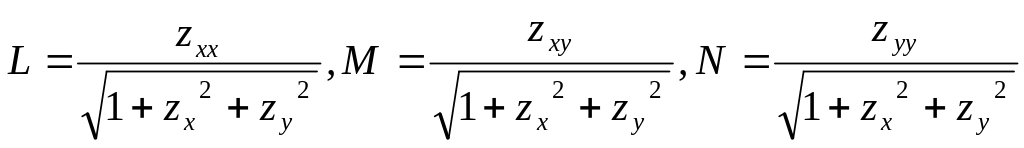 .
Для коэффициентов II кв. формы используются
также обозначения:
.
Для коэффициентов II кв. формы используются
также обозначения:
![]() .
Матрицу
.
Матрицу
![]() называют матрицей II квадратической
формы. Квадр. форму можно подать в виде:
II=
называют матрицей II квадратической
формы. Квадр. форму можно подать в виде:
II=![]() ,
где
,
где
![]() ,
,
![]() ,
,
![]() .
Нормальным сечением
.
Нормальным сечением![]() поверхности S в т. Р называется пересечение
поверхности с плоскостью, проходящей
через нормаль поверхности в этой точке.
поверхности S в т. Р называется пересечение
поверхности с плоскостью, проходящей
через нормаль поверхности в этой точке.
![]() .
Из этого следует, что
.
Из этого следует, что
![]() .
.
График:
Нормальной
кривизной КH
кривой, лежащей на поворот, в ее точке
М называется скалярная проэкция вектора
кривизны кривой в этой точке на нормаль
поверхности. Нормальная кривизна кривой
на S совпадает с точностью до знака с
кривизной нормального сечения
поверхности, имеющего с кривой
![]() общую касательную и вычисляется по
формуле:
общую касательную и вычисляется по
формуле:
![]() .
Формула Менье:
.
Формула Менье:
![]() .
Нормальная кривизна кривой зависит от
вектора скорости кривой:
.
Нормальная кривизна кривой зависит от
вектора скорости кривой:
![]() .
.
61. Сравнения по простому и составному модулю. Решение сравнений.
Два
целых числа а и в сравнимы по модулю
натурального числа m
є
N, если при делении на m они дают одинаковый
остаток.
![]() .
.
Теорема
(критерий сравнимости):
![]() .
Следствие 1: каждое число сравнимо по
модулю m со своим остатком от деления
на m:
.
Следствие 1: каждое число сравнимо по
модулю m со своим остатком от деления
на m:
![]() .
Следствие 2: число сравнимо по модулю
m, т. и т. т., к. оно делится на этот mod.
.
Следствие 2: число сравнимо по модулю
m, т. и т. т., к. оно делится на этот mod.
Основные
свойства сравнения: 1). Относительные
сравнения являются относительно
эквивалентными. 2). Сравнения по одному
и тому же модулю можно почленно вычитать:
![]() .
Слагаемое можно переносить из одной
части в другую, при этом знак меняем на
противоположный. 3). В каждой части
сравнения можно прибавлять любое число,
кратное модулю:
.
Слагаемое можно переносить из одной
части в другую, при этом знак меняем на
противоположный. 3). В каждой части
сравнения можно прибавлять любое число,
кратное модулю:
![]() сравнения по одному и тому же модулю
можно почленно умножать. Следствия: 1.
Обе части сравнения можно возводить в
любую натуральную степень. 2. Обе части
сравнения можно умножать на любое
натуральное число. 4). Обе части сравнения
и модуль можно умножить на одно и то же
число или сократить на любой их общий
делитель. 5). Если сравнение имеет место
по нескольким модулям то оно имеет место
и по модулю, который равен их наибольшему
кратному или наибольшему общему делителю
сравнения по одному и тому же модулю
можно почленно умножать. Следствия: 1.
Обе части сравнения можно возводить в
любую натуральную степень. 2. Обе части
сравнения можно умножать на любое
натуральное число. 4). Обе части сравнения
и модуль можно умножить на одно и то же
число или сократить на любой их общий
делитель. 5). Если сравнение имеет место
по нескольким модулям то оно имеет место
и по модулю, который равен их наибольшему
кратному или наибольшему общему делителю![]()
