2.3. Параболічні рівняння.

Прикладом задачі, що зводиться до параболічного рівняння в частинних похідних, може бути задача про теплопередачу у довгому стрижні. Вона описується рівнянням теплопередачі (або дифузії).

Задача полягає в знаходженні f (x, t), яка задовольняє скрізь у області Ω={(x, t) | 0 ≤ x ≤ a, 0 ≤ t ≤ T } рівняння

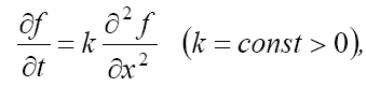
початкові

f (x, 0)=f0 (x)

і граничні умови першого роду

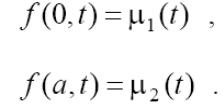
Бачимо, що заміна змінної t = k t приводить рівняння до вигляду

тому надалі будемо вважати k=1.

Можливі два варіанти отримання різницевого рівняння на сітці з кроком h по x та τ по t (рисунок 5).

Рис. 5. Обчислювальні шаблони для параболічних рівнянь.

Варіант з апроксимацією на чотириточковому шаблоні (рисунок 5а) приводить до неявної двошарової різницевої схеми

2 fi+1, j − (1 + 2r)fi, j + 2 fi−1, j = − fi, j−1 ,

де .

Ця схема доповнена рівняннями, отриманими з крайових умов

f0, j = μ1 (t j ); fn, j = μ2 (t j ),

зводить задачу до розв’язання системи рівнянь, які мають стійкий розв’язок при будь-яких значеннях r.

Варіант із апроксимацією на чотириточковому шаблоні (рисунок 5б) призводить до явної двошарової системи

fi, j+1 = rfi+1, j + (1 − 2r) fi, j + 2 fi−1, j.

Ця схема стійка тільки при r ≤ 0,5, що змушує проводити обчислення з дуже малим кроком по t, а це обмежує швидкодію і вимагає більших затрат часу ПЕОМ. Тому для параболічних рівнянь набагато ширше розповсюдження отримала неявна схема.

3. Загальні рекомендації до розв’язування

диференційних рівнянь у частинних похідних.

На початковому етапі вибирається метод розв’язання задачі. Зазвичай простіше використовувати різницевий метод, який вимагає простішої підготовки задачі до розв’язання, але в ряді випадків для задач із добре розробленою теорією (наприклад, задач механіки) доцільно звертатися до методу скінченних елементів.

При визначенні кроку розв’язання задачі основним фактором є точність (якщо висока, то необхідна або дуже дрібна сітка, або розбиття на дуже малі елементи). При цьому необхідно враховувати, що похибка різницевих методів має другий порядок. Її оцінку можна проводити аналогічно звичайним диференційним рівнянням за методом Рунге.

У випадку симетрії число вузлів можна зменшити в два або навіть у чотири рази (при симетрії по обох осях координат). Велику роль для ефективного розв’язання задачі грає вибір початкових наближень. При використанні ітераційних методів від цього значною мірою залежить швидкість збігання. Часто має сенс розв’язувати задачу в декілька етапів: на першому за допомогою «грубої» сітки (або розбиття на крупні елементи) отримують добре початкове наближення, на наступних – шукають більш точний розв’язок на дрібній сітці.

Індивідуальні завдання

Використовуючи метод сіток, побудувати різницеву схему для заданої крайової задачі. Одержану СЛАР розв’язати методом прогонки.

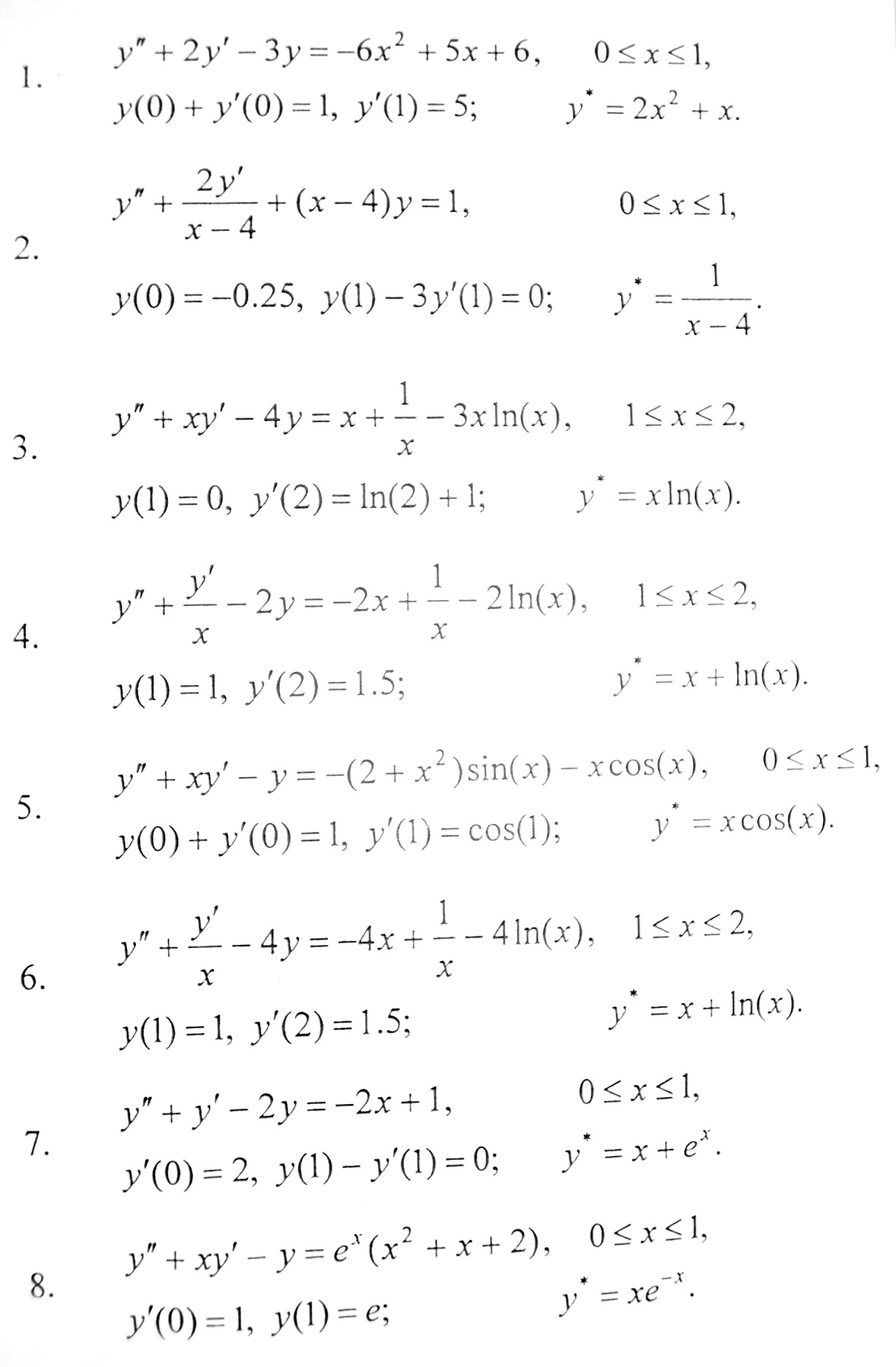
Контрольні запитання

1. Наведіть приклади інженерних або управлінських задач, які описуються диференційними рівняннями в частинних похідних.

2. На які типи можна поділити диференційні рівняння другого порядку в частинних похідних в залежності від коефіцієнтів, які входять до них?

3. Які методи розв’язування диференційних рівнянь в частинних похідних Ви знаєте?

4. Як конструюються обчислювальні шаблони для частинних похідних? Отримайте обчислювальні шаблони для оператора Лапласа та бігармонійного оператора.

5. Як використовується різницевий метод у випадку, коли границя області, де шукають розв’язок, не проходить через вузли сітки? Наведіть приклад обчислювального шаблону?

6. Якими різницевими методами розв’язується класична задача Діріхле для рівнянь Лапласа в прямокутній області?

7. В яких випадках розв’язок стійкий для тришарової схеми розв’язання гіперболічних рівнянь. ?

8. Порівняйте ефективність використання явної і неявної схем розв’язування параболічних рівнянь у частинних похідних.

9. Як вибирається крок при розв’язуванні диференційних рівнянь у частинних похідних?