2 Случай. Аналогично случаю 1 имеем:

, , ,

откуда

.

Ответ: или .

Ваша оценка (баллов):

Содержание критериев оценивания задачи С5	Баллы
Обоснованно получен верный ответ.	4
Рассмотрены все возможные случаи. Получен верный ответ, но решение либо содержит пробелы, либо вычислительную ошибку или описку.	3
Рассмотрены все возможные случаи. Получен ответ, но решение содержит ошибки.	2
Рассмотрены некоторые случаи. Для рассмотренных случаев получен ответ, возможно неверный из-за ошибок.	1
Все прочие случаи.	0

Найдите все значения а, при каждом из которых множеством решений неравенства является отрезок.

Решение:

Перепишем неравенство в виде

,

и нарисуем эскизы графиков левой и правой частей неравенства.

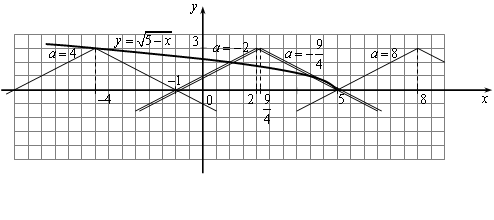
Рассматривая взаимное расположение графиков при разных а, получаем:

или .

Ответ: .

Ваша оценка (баллов):

Содержание критериев оценивания задачи С6	Баллы
Обоснованно получен верный ответ.	4
Решение не содержит логических пробелов, получен ответ, неверный только из-за вычислительной ошибки или описки.	3
Решение доведено до ответа, но содержит логические пробелы, вычислительные ошибки или описки.	2
Расмсотрены и проверены отдельные части ответа.	1
Все прочие случаи.	0

Каждое из чисел 2, 3, ... , 7 умножают на каждое из чисел 13, 14, ... , 21 и перед каждым из полученных произведении произвольным образом ставят знак плюс или минус, после чего все 54 полученных результата складывают. Какую наименьшую по модулю и какую наибольшую сумму можно получить в итоге?

Решение:

1. Если все произведения взяты со знаком плюс, то их сумма максимальна и равна

.

2. Так как сумма оказалась нечетной, то чисто нечетных слагаемых в ней нечетно, причем это свойство всей суммы не меняется при смене знака любого ее слагаемого. Поэтому любая из получающихся сумм будет нечетной, а значит, не будет равна 0. 3. Значение 1 сумма принимает, например, при такой расстановке знаков у произведений, которая получится при раскрытии следующих скобок:

.

Ответ: 1 и 4131.

Ваша оценка (баллов):