
- •Детали машин и основы конструирования
- •Механические передачи
- •Основные характеристики передач
- •Фрикционные передачи и вариаторы
- •Основы прочностного расчета фрикционных пар
- •Зубчатые передачи
- •Коэффициент торцового перекрытия έα
- •Расчетная нагрузка
- •Коэффициент концентрации нагрузки kβ
- •Коэффициент динамической нагрузки kν
- •Расчет прочности зубьев по контактным напряжениям
- •Силы, действующие на зуб колеса
- •Удельная нагрузка
- •Расчет прочности зубьев косозубой передачи по контактным напряжениям
- •Расчет прочности зубьев косозубых передач по напряжениям изгиба
- •Материалы и термообработка
- •Допускаемые напряжения материалов зубчатых колес
- •Допускаемые контактные напряжения [σH] при расчете зубчатых колес на усталость
- •Допускаемое напряжение изгиба при расчете на усталость
- •Последовательность расчета косозубой цилиндрической передачи по контактным напряжениям
- •Конические зубчатые передачи
- •Силы в зацеплении прямозубой конической передаче
- •Приведение прямозубого конического колеса к эквивалентному прямозубому цилиндрическому
- •Р асчет зубьев прямозубой конической передачи по напряжениям изгиба
- •Расчет зубьев прямозубой конической передачи по контактным напряжениям
- •Конические передачи с непрямыми зубьями
- •Червячные передачи
- •Основные геометрические параметры
- •Силы в зацеплении
- •Расчет на прочность червячных передач
- •Расчет на прочность по контактным напряжениям
- •Р еменные передачи
- •Критерии работоспособности
- •Силовые зависимости
- •Допускаемые полезные напряжения в ремне
- •К линоременная передача
- •Межосевое расстояние и длина цепи
- •Практический расчет цепной передачи
- •Передача винт-гайка
- •Передача винт-гайка качения
- •Подшипники
- •Расчет на долговечность
- •Условия подбора
- •Эквивалентная динамическая нагрузка
- •Проверка и подбор подшипников по статической грузоподъемности (с0)
- •Подшипники скольжения
- •Классификация муфт
- •Муфты глухие
- •Муфты компенсирующие
- •Муфты компенсирующие упругие
- •Муфты управляемые или сцепные
- •Муфты фрикционные
- •Муфты автоматические, или самоуправляемые
- •Соединения
- •С оединение сегментной шпонкой
- •Общие замечания по расчету призматических шпоночных соединений
- •Резьбовые соединения
- •Расчет на прочность стержня винта (болта) при различных случаях нагружения
- •З аклепочные соединения
- •Сварные соединения
Основы прочностного расчета фрикционных пар
Критерии работоспособности:
Усталостное выкрашивание
Износ
Задир поверхности
Усталостное выкрашивание происходит в ходе нормальной длительной эксплуатации передачи работающей с обильной смазкой. Износ является следствием скудной смазки, а задир поверхности происходит как результат буксования или перегрева.
Все перечисленные виды разрушения поверхности катков зависят от напряжений в месте контакта. Поэтому прочность и долговечность оценивают по контактным напряжениям.
Контактные
напряжения образуются в месте
соприкосновения двух тел в тех случаях,
когда размеры площадки касания малы по
сравнению с размерами тел. Основоположником
теории контактных напряжений является
немецкий механик H.
Herz.
Контактные
напряжения записываются σ![]() ,
где индекс обозначен в честь ученого.
Рассмотрим пример сжатия 2-х цилиндров
(см. рис.)
,
где индекс обозначен в честь ученого.
Рассмотрим пример сжатия 2-х цилиндров
(см. рис.)
Формула Герца для расчета контактных напряжений при сжатии двух цилиндров:
![]() .
.
Здесь
![]() ;
;
![]() ;
;
![]() .
.
+ – для выпуклых поверхностей;
- – для вогнутых поверхностей.
При контакте
цилиндра с плоскостью r2
=
![]()
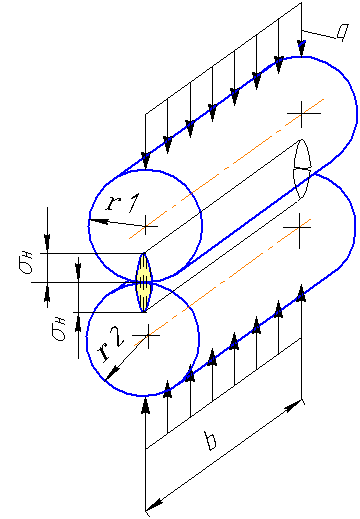
Где q – нагрузка на единицу длины контактной линии;
r1 u r2 – радиусы цилиндров;
b –длина контактной линии (длина цилиндров).
При вращении цилиндров (например, катков фрикционных пар) отдельные точки их поверхностей периодически нагружаются и разгружаются. Контактные напряжения в этих точках изменяются по прерывистому отнулевому циклу (см. рис.).
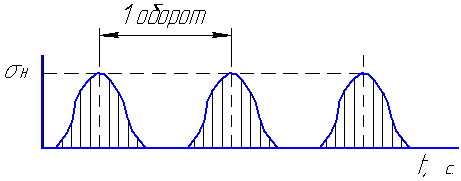
Это вызывает усталость поверхностных слоев деталей. Образуются микротрещины, и происходит выкрашивание мелких частиц металла. Чтобы не было усталостного малоциклового разрушения нужно ограничить величину контактных напряжений, т.е. выполнить условие:
![]() ,
,
где
![]() - допускаемое контактное напряжение.
- допускаемое контактное напряжение.
Условие прочности для контакта цилиндров по линии запишется:
![]() .
.
Это выражение используется для проверочного расчета, когда известна геометрия передачи, т.е. ее размеры, материалы и нагрузки.
Допускаемые напряжения.
Для закаленной
стали при твердости поверхности H1,2![]()
![]() = 1000…1200 МПа.
= 1000…1200 МПа.
Для текстолита
= 80 …100 МПа.
При проектном расчете фрикционной передачи определяются ее размеры. Межосевое расстояние «а» между катками находят из выражения:
![]() ,
,
где i – передаточное отношение без учета знака;
![]() коэффициент
ширины катка, выбираемый по рекомендациям.
коэффициент
ширины катка, выбираемый по рекомендациям.
При известном «a» находят другие размеры передачи по формулам:
![]() ;
;
![]() ;
;
![]()
ЛЕКЦИЯ № 4
Зубчатые передачи
Зубчатая передача представляет собой механизм, который с помощью зацепления передает (а иногда преобразует) движение с изменением угловых скоростей и моментов.
По расположению валов и зубьев на колесах зубчатые передачи бывают с параллельными, пересекающимися и перекрещивающимися валами; прямозубые, косозубые и с круговым зубом (по плакату).
По форме профиля зуба: эвольвентные, круговые (системы Новикова) и циклоидные. Эвольвентные профили зуба предложены Эйлером в 1760 году.
По условиям работы зубчатой передачи они могут быть открытыми (незащищенными от внешней среды) и закрытыми. К последним относятся редукторы, коробки скоростей и др. передачи, работающие в масляной ванне.
Достоинства зубчатых передач:
Высокая нагрузочная способность, т.е. малые габариты;
Большая долговечность и надежность работы при высоком КПД: 0,97-0,98 в одной ступени;
Постоянство передаточного отношения и др.
Недостатки:
Повышенные требования к точности изготовления;
Шум при больших частотах вращения.
Наибольшее распространение имеют передачи с цилиндрическими колесам, как наиболее простые и надежные.
Стандарты устанавливают термины, определения и обозначения, а также методы расчета геометрических параметров.
Шестерня – это меньшее из пары зубчатых колес.
Колесо – большее из пары зубчатых колес.
Параметрам шестерни приписывают индекс 1, а параметрам колеса индекс 2 (рисунок с картиной зацепления). Кроме того, индексы:
w – к начальной поверхности или окружности;
b – к основной поверхности или окружности;
a – к поверхности или окружности вершин и головок зубьев;
f – к поверхности или окружности впадин и ножек зубьев.
Параметрам, относящимся к делительной поверхности или окружности, дополнительного индекса не приписывают.
z1 и z2 – число зубьев шестерни и колеса;
P – делительный окружной шаг зубьев;
Pb=P cosα – основной окружной шаг;
α – угол профиля делительный (угол профиля исходного контура), α=20º;
αw – угол зацепления или угол профиля начальный
aw cosαw= a cosα,
m = P/π – окружной модуль зубьев. Значения модулей стандартизованы, π =3,14.
Картина зацепления:
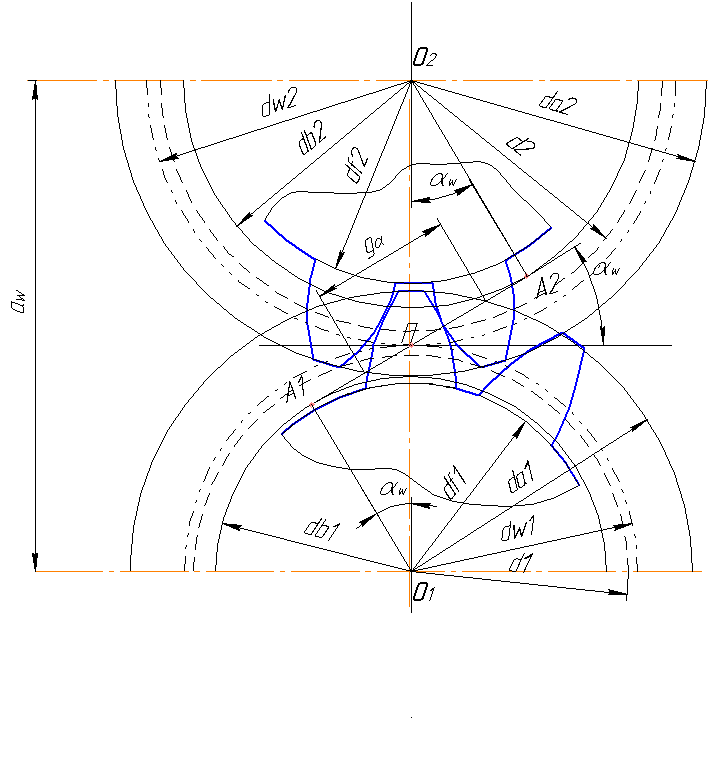
![]() –
делительный диаметр
– диаметр окружности, по которой
обкатывает инструмент при нарезании
зубьев;
–
делительный диаметр
– диаметр окружности, по которой
обкатывает инструмент при нарезании
зубьев;
![]() – основной диаметр
– диаметр окружности, разверткой которой
являются эвольвенты зубьев;
– основной диаметр
– диаметр окружности, разверткой которой
являются эвольвенты зубьев;
![]() и
и
![]() – начальные диаметры – диаметры, по
которым пара зубчатых колес обкатывается
в процессе вращения;
– начальные диаметры – диаметры, по
которым пара зубчатых колес обкатывается
в процессе вращения;
![]()
![]() .
.
У передач без
смещения и при нулевом суммарном смещении
(x![]() =
0) начальные и делительные окружности
совпадают, т.е.
=
0) начальные и делительные окружности
совпадают, т.е.
![]() ;
;
![]() .
.
При
резании
колес со смещением делительная плоскость
рейки (инструмента) смещается к центру
или от центра заготовки на
![]() ;
;
![]() –
коэффициент смещения исходного контура.
Смещение от центра считается положительным
(
>0),
а к центру – отрицательным (
<0).
–
коэффициент смещения исходного контура.
Смещение от центра считается положительным
(
>0),
а к центру – отрицательным (
<0).
![]() – межосевое
расстояние
– межосевое
расстояние
![]() ,
,
где
![]() ;
;
![]() –
коэффициент
уравнительного смещения при
–
коэффициент
уравнительного смещения при
![]() .
.
Для колес без смещения:
h = 2,25m;
da = d + 2m;
d f= d – 2,5m;
hГ =1m;
hH =1,25m,
г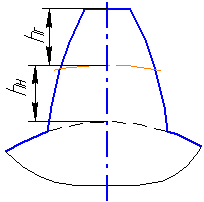 де
h
,hГ
, hН
– высота
зуба, высота головки и высота ножки зуба
соответственно.
де
h
,hГ
, hН
– высота
зуба, высота головки и высота ножки зуба
соответственно.
Линия зацепления A1-A2 – это общая касательная к основным окружностям пары зубчатых колес.
gα – длина активной части линии зацепления;
П – полюс зацепления.
z2/z1 = u (по ГОСТ 16532-70) – передаточное число. Отношение большего числа зубьев к меньшему числу независимо от того, как передается движение. u = z2/z1 = dw2/dw1 > 1.
