
- •Детали машин и основы конструирования
- •Механические передачи
- •Основные характеристики передач
- •Фрикционные передачи и вариаторы
- •Основы прочностного расчета фрикционных пар
- •Зубчатые передачи
- •Коэффициент торцового перекрытия έα
- •Расчетная нагрузка
- •Коэффициент концентрации нагрузки kβ
- •Коэффициент динамической нагрузки kν
- •Расчет прочности зубьев по контактным напряжениям
- •Силы, действующие на зуб колеса
- •Удельная нагрузка
- •Расчет прочности зубьев косозубой передачи по контактным напряжениям
- •Расчет прочности зубьев косозубых передач по напряжениям изгиба
- •Материалы и термообработка
- •Допускаемые напряжения материалов зубчатых колес
- •Допускаемые контактные напряжения [σH] при расчете зубчатых колес на усталость
- •Допускаемое напряжение изгиба при расчете на усталость
- •Последовательность расчета косозубой цилиндрической передачи по контактным напряжениям
- •Конические зубчатые передачи
- •Силы в зацеплении прямозубой конической передаче
- •Приведение прямозубого конического колеса к эквивалентному прямозубому цилиндрическому
- •Р асчет зубьев прямозубой конической передачи по напряжениям изгиба
- •Расчет зубьев прямозубой конической передачи по контактным напряжениям
- •Конические передачи с непрямыми зубьями
- •Червячные передачи
- •Основные геометрические параметры
- •Силы в зацеплении
- •Расчет на прочность червячных передач
- •Расчет на прочность по контактным напряжениям
- •Р еменные передачи
- •Критерии работоспособности
- •Силовые зависимости
- •Допускаемые полезные напряжения в ремне
- •К линоременная передача
- •Межосевое расстояние и длина цепи
- •Практический расчет цепной передачи
- •Передача винт-гайка
- •Передача винт-гайка качения
- •Подшипники
- •Расчет на долговечность
- •Условия подбора
- •Эквивалентная динамическая нагрузка
- •Проверка и подбор подшипников по статической грузоподъемности (с0)
- •Подшипники скольжения
- •Классификация муфт
- •Муфты глухие
- •Муфты компенсирующие
- •Муфты компенсирующие упругие
- •Муфты управляемые или сцепные
- •Муфты фрикционные
- •Муфты автоматические, или самоуправляемые
- •Соединения
- •С оединение сегментной шпонкой
- •Общие замечания по расчету призматических шпоночных соединений
- •Резьбовые соединения
- •Расчет на прочность стержня винта (болта) при различных случаях нагружения
- •З аклепочные соединения
- •Сварные соединения
Допускаемое напряжение изгиба при расчете на усталость
Расчет допускаемого напряжения изгиба ведется по формуле:
![]() ,
,
где σF0 – предел выносливости зубьев по напряжениям изгиба. Определяется экспериментально по кривой усталости для зубчатых колес
SF = 1,55…1,75 – коэффициент безопасности.
KFC – коэффициент влияния двухстороннего приложения нагрузки (реверсивная передача и т.п.).
KFC = 1 – для односторонней нагрузки;
KFC = 0,7…0,8 – для реверсивной нагрузки.
KFL – коэффициент долговечности.
![]() ,
,
где базовое число
циклов для всех сталей
![]() .
.
![]() – для зубчатых
колес с твердостью поверхности
– для зубчатых
колес с твердостью поверхности
зубьев
![]() ;
;
– для зубчатых колес со шлифованной переходной поверхностью независимо от твердости и термообработки;
![]() – для зубчатых
колес Н >
350 НВ с нешлифованной
– для зубчатых
колес Н >
350 НВ с нешлифованной
переходной поверхностью.
![]()
![]()
 ,
,
или NFE = KFE NΣ .
Как уже отмечалось ранее, расчет на прочность ведется по материалу, для которого меньшим является отношение допускаемого напряжения изгиба к величине коэффициента формы зуба, т.е.
или .
Последовательность расчета косозубой цилиндрической передачи по контактным напряжениям
Выбор материалов и термообработки. Определение допускаемого напряжения
 .
.Задание и расчет коэффициентов ψва и КНβ.
Расчет межосевого расстояния «а» и округление до стандартного значения аw из ряда Ra 20 или Ra 40.
Определение ширины зубчатого венца колеса
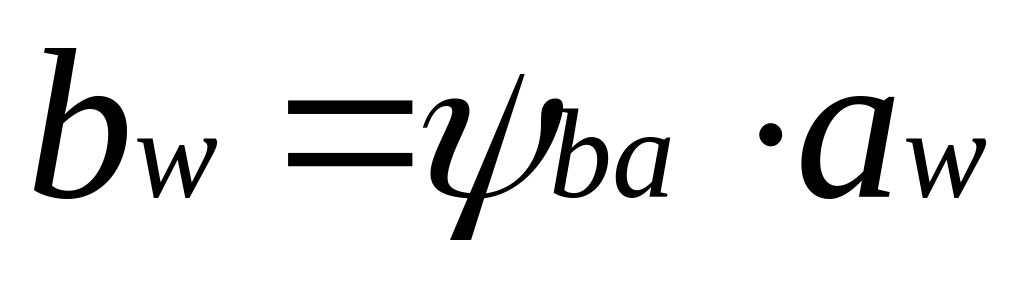 .
.Выбор или расчет коэффициента ψm.
Расчет модуля mn=bw/ψm. Выбор стандартного значения.
Задаемся εβ = 1,1…1,2 и вычисляем:
 .
.Вычисляем β': β'=arcsin(
 ).
Находим cos
β'
(до 4-го знака).
).
Находим cos
β'
(до 4-го знака).Суммарное число зубьев:
 (округлить до целого числа).
(округлить до целого числа).
Коррекция угла наклона зуба:
 ( находим до 4-го знака). Вычисляем
уточненное значение угла β.
( находим до 4-го знака). Вычисляем
уточненное значение угла β.Число зубьев шестерни:
 (округляем до целого числа).
(округляем до целого числа).Число зубьев колеса: z2=z
 –
z1
.
–
z1
.Расчет делительных диаметров:
![]()
14. Передаточное число: u = z2/z1 . Проверить отклонение от заданного значения.
Пример расчета пределов выносливости σн0 и σF0 по твердости материалов зубчатых колес
Сталь |
Термообработка |
Твердость зуба |
σн0 |
σF0 |
45, 40Х и др. |
Нормализация, Улучшение |
180…350НВ |
|
|
Объемная заклка |
45…55HRC |
|
550 |
ЛЕКЦИЯ №11
Конические зубчатые передачи
Применяются в случаях, когда оси валов пересекаются под некоторым углом Σ (чаще всего это 90º).
К онические
передачи сложнее в изготовлении и
монтаже. Требуются специальные станки
и специальный инструмент. Кроме допусков
на размеры нужны допуски на углы (Σ,
δ1 и δ2),
а при монтаже обеспечить совпадение
вершин конусов. По опытным данным
нагрузочная способность конической
прямозубой передачи составляет 0,85 от
цилиндрической передачи.
онические
передачи сложнее в изготовлении и
монтаже. Требуются специальные станки
и специальный инструмент. Кроме допусков
на размеры нужны допуски на углы (Σ,
δ1 и δ2),
а при монтаже обеспечить совпадение
вершин конусов. По опытным данным
нагрузочная способность конической
прямозубой передачи составляет 0,85 от
цилиндрической передачи.
Аналогами начальных и делительных цилиндров цилиндрических передач в конических передачах являются начальные и делительные конусы с углами δ1 и δ2. При коэффициентах смещения инструмента x1 + x2 = 0 начальные и делительные конусы совпадают.
Конусы, образующие которых перпендикулярны образующим делительных конусов, называют дополнительными конусами. Сечение зубьев дополнительным конусом называют торцовым сечением. Размеры, относящиеся к внешнему торцовому сечению, имеют индекс “е”, например, de. Размеры в среднем сечении сопровождают индексом “m”.
Re и Rm – внешнее и среднее конусные расстояния;
b – ширина зубчатого венца.
Р![]() азмеры
по внешнему торцу удобнее для измерения,
их указывают на чертежах. Размеры в
среднем сечении используют при силовых
расчетах. Соотношения размеров в среднем
и торцовом сечениях:
азмеры
по внешнему торцу удобнее для измерения,
их указывают на чертежах. Размеры в
среднем сечении используют при силовых
расчетах. Соотношения размеров в среднем
и торцовом сечениях:
Для прямозубых
передач торцовое «t»
и нормальное «n»
сечения совпадают. При этом
![]() округляют до стандартного значения.
округляют до стандартного значения.
Передаточное число. Как и у цилиндрических передач
![]()
Так как
![]() и
и
![]() ,
то можно записать:
,
то можно записать:
![]() а при Σ = δ1 + δ2 =
90º имеем:
а при Σ = δ1 + δ2 =
90º имеем:
![]()
