Р а з д е л 2. Теплопроводность

2.1. Общие положения теории теплопроводности

Теплопроводность веществ

Как указывалось ранее, основной закон теплопроводности формулируется так: плотность теплового потока пропорциональна градиенту температуры, то есть

(2.1)

В этом уравнении множитель - это коэффициент теплопроводности, характеризующий способность вещества передавать энергию и определяющий её количество, которое проходит в единицу времени через единицу поверхности при падении температуры на один градус на единице длины нормали.

Для различных материалов неодинаковые: каждая из них зависит от структуры, плотности, влажности, давления и температуры. В большинстве случаев эти величины устанавливаются экспериментальным путем. Чтобы оценить, насколько различна способность проводить теплоту, укажем значения для некоторых веществ (табл.2.1). Так для слоя неподвижного воздуха при комнатной температуре =0,02 Вт/(м град), алюминия – 200, золота -300, меди – 386 и для серебра – 410 Вт/(м град). Одним из наименее теплопроводных чистых металлов является титан (15Вт/(м град)). Железо обладает средней теплопроводностью 95 Вт/(м град).

Таблица 2.1. Значения коэффициента теплопроводности материалов

Наименование материала	Значение показателя (Вт/(м град))
Медь	386
Алюминий	200
Углеродистая сталь	50
Огнеупорный кирпич	1-5
Стекло	0,75
Пластмассы	0,2-0,45
Вода	0,6
Моторное масло	0,15
Мазут	0,12
Огнеупорный изоляционный материал	0,2-0,03
Воздух	0,02

С увеличением температуры значение для чистых металлов падает, а при наличии примесей в сталях влияние её будет различно.

Плохими проводниками являются строительные и теплоизоляционные материалы ( =5-0,03 Вт/(м град)), что объясняется их высокой пористостью.

У твердых неметаллических материалов, а также теплоизоляционных материалов при высоких температурах, значение  увеличивается с увеличением температуры.

У жидкостей коэффициент теплопроводности уменьшается с увеличением температуры (кроме воды и глицерина).

Теплопроводность газов значительно увеличивается с ростом температуры. Значения теплопроводности для газов колеблются примерно в диапазоне от 0,006 до 0,1 Вт/(м град). Исключение составляют водород и гелий, теплопроводность которых в 5-10 раз выше, чем у остальных газов.

Анализ зависимости коэффициента теплопроводности от температуры показывает, что для большинства твердых тел, жидкостей и газов при умеренных температурах эта зависимость приближенно может быть оценена линейной формулой

(2.2)

где - коэффициент теплопроводности материала при t = 0 C⁰ , - экспериментальная константа.

Дифференциальное уравнение теплопроводности Фурье

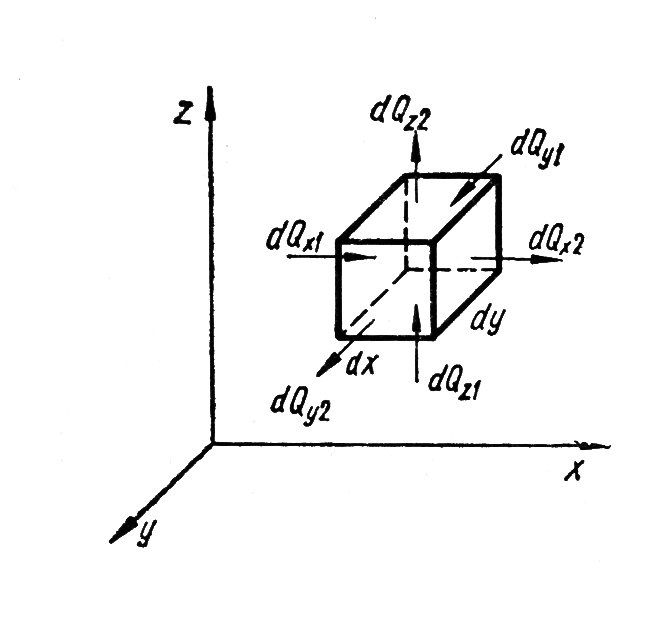
Рис. 2. К выводу дифференциального уравнения теплопроводности

Дифференциальное уравнение теплопроводности Фурье является математическим выражением закона сохранения энергии. Оно выводится из рассмотрения баланса энергии для элементарного объема материала, в котором происходит перенос теплоты теплопроводностью. При составлении баланса энергии учитывается возможное генерирование энергии внутри материала (тепловыделение при физико-химических превращениях, нагрев при пропускании через тело электротока)

Физической основой вывода уравнения теплопроводности служит следующая формулировка баланса энергии: Сумма энергии подводимой к элементарному объему вследствие теплопроводности и генерируемой внутри его равна сумме энергий отводимой из элементарного объема вследствие теплопроводности и аккумулированной внутри ее.

Решаем задачу в прямоугольной системе координат. Предположим, что рассматриваемое тело - изотропное, температурные деформации элементарного объема пренебрежимо мало и температурное поле стационарно. Материал тела характеризуется коэффициентом теплопроводности , теплоемкостью c и плотностью .

Обозначим составляющие теплового потока за время ,

а составляющие покидающие объем - . Согласно определению плотности теплового потока: количество теплоты, подводимое к элементному объему вследствие теплопроводности:

Соответственно количество теплоты, отводимое из элементарного объема:

Тогда изменение теплосодержания объема dV за время d вызванное теплопроводностью составит:

(2.3)

Плотности потоков и , и , и незначительно отличается. Поэтому каждую из них можно вблизи с точкой с координатами x,y,z разложить в ряд Тейлора по степеням dx,dy,dz.

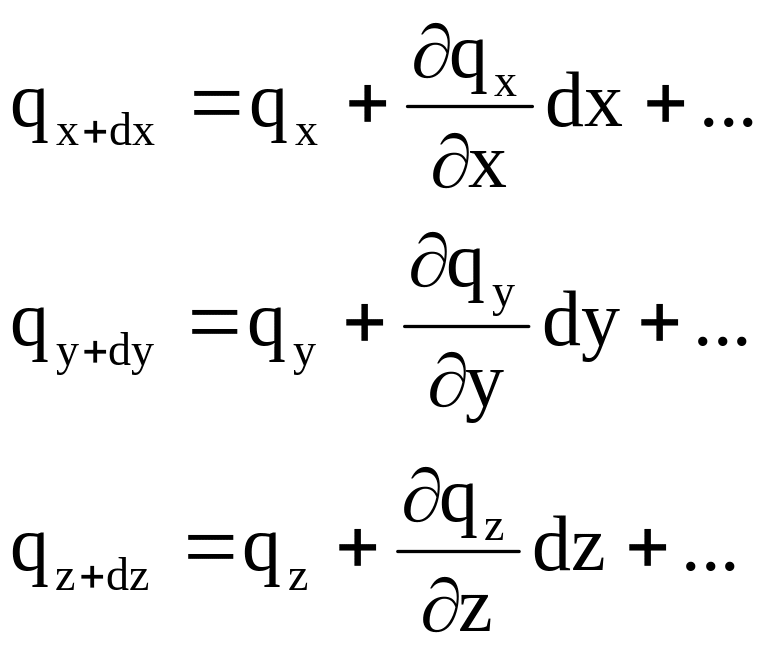(2.4)

После подстановки (2) в (1) получим:

(2.5)

Генерация энергии в элементарном объеме может быть охарактеризована объемной плотностью теплового потока, которая определяется как количество теплоты, выделяемое (поглощаемое) внутренними источниками в единице объема в единицу времени q_v (Вт/м³). Тогда количество теплоты, генерируемое в элементарном объеме за время , составит:

(2.6)

Количество энергии, аккумулированное в элементарном объеме равно:

(2.7)

В зависимости от характера движения среды, в которой протекает процесс, содержание полного дифференциала температуры разное. Для твердого тела

, (2.8)

а для жидкости:

, (2.9)

где - проекция вектора скорости среды на оси прямоугольной системы координат.

Согласно физической постановке уравнение баланса энергии принимает вид:

(2.10)

После подстановки составляющих уравнения баланса, имеем

.

Учитывая принятые в математическом анализе понятия градиента, дивергенции и оператора Лапласа

; ,

получим классическое уравнение Фурье-Кирхгофа в виде:

. (2.11)

Такая форма записи справедлива для любой среды (движущейся и неподвижной) и любой системы координат. Если необходим учет зависимости теплофизических свойств от температуры, то уравнение переноса следует представлять в виде

.

Если значения неизменны, то дифференциальное уравнение теплопроводности имеет вид

;

, (2.12)

где а - коэффициент температуропроводности характеризует скорость изменения температуры тела и является мерой теплоинерционных свойств.

Из анализа уравнения следует, что скорость изменения температуры будет тем больше, чем больше коэффициент температуропроводности.. При прочих равных условиях скорость выравнивания температур будет больше в тех телах, где значение этой величины выше.

Для твердых тел с учетом (2.8) дифференциальное уравнение теплопроводности принимает вид:

;

; (2.13)

Для движущейся среды, после раскрытия содержания полного дифференциала согласно соотношению (2.9), уравнение переноса принимает вид:

, (2.14)

где - составляющие скорости движения точки.

Если генерация энергии в твердом теле отсутствует ( ), то уравнение (2.13) называется дифференциальным уравнением теплопроводности Фурье и выглядит так

; . (2.15)

В случае одномерных задач дифференциальное уравнение теплопроводности Фурье записывается в виде:

- для пластины ; (2.16)

- для цилиндра ; (2.17)

- для сферы . (2.18)

В общем случае дифференциальное уравнение имеет бесчисленное множество решений, и чтобы выделить из него то, которое описывает интересующий нас процесс, в уравнении необходимо добавить условия однозначности, которые включают геометрические характеристики объекта (форма и линейные размеры), теплофизические характеристики , а также краевые условия.

Краевыми условиями называют совокупность начального и граничного условия, а отыскание решений с учетом этих условий – краевой задачей математической физики.

Начальные условия задаются только для нестационарных процессов и содержат распределение температуры внутри тела в начальный момент времени. Математически начальные условия записываются в таком виде:

(2.19)

Наиболее простой случай, имеющий практическое значение, соответствует одинаковым значения температур по всему объему тела:

.

Граничные условия отображают условия теплового взаимодействия между окружающей средой и поверхностью тела. Известны четыре рода указанных условий.

Граничные условия I-го рода состоят в задании температуры на поверхности тела как функции координат и времени.

, ,

где - поверхность тела. Примером граничных условий I-го рода является постоянство температуры поверхности

С некоторым приближением граничные условия I-го рода можно отнести к задачам нагрева и охлаждения тел при заданном изменении температуры поверхности, когда эти процессы протекают достаточно медленно, или при весьма интенсивном теплообмене на поверхности, когда температура поверхности близка к температуре среды.

Граничные условия II-го рода состоят в задании плотности теплового потока на поверхность тела как функции координат и времени

, (2.20)

Примером граничных условий II рода является постоянство указанной плотности:

.

С достаточной точностью подобные условия теплообмена реализуются при нагревании тел в высокотемпературных печах, когда теплообмен происходит излучением. Граничные условия II-го рода находят частое применение при выравнивании температур в теплоизолированных системах, а также при решении задач симметричного нагрева и охлаждения.

Граничные условия III-го рода состоят в задании зависимости плотности теплового потока вследствие теплопроводности со стороны тела от температуры поверхности, температуры среды и закона теплообмена. Плотность теплового потока отводимого за счет теплопроводности от поверхности тела определяется законом Фурье. Для описания теплообмена между поверхностью тела и средой используется гипотеза Ньютона – Рихмана. Приход теплоты равен её расходу вследствие закона сохранения энергий. С учетом этого граничное условие III рода запишется в виде:

. (2.21)

Граничные условия IV-го рода (условие сопряжения) соответствует теплообмену соприкасающихся твердых тел. Задаются как равновесие температур (условие неразрывности температурного поля) и тепловых потоков (сохранения энергии на поверхности соприкосновения) в месте контакта:

;

. (2.22)