1.4.56. В механизме (рис. 112)

шкив 1 радиуса r = 0,1 м шарнирно

Р ис. 111 соединен со стержнем 2 длиной 0,25 м с помощью штанги АВ. Для данного положения механизма определить угловую скорость штанги, если частота вращения шки­ва 1 равна 120 об/мин, а

расстояние 0₁0₂ = 0,45м. (2,28).

Рис. 112

Рис. 113 Рис. 114

1.4.57. На ось А независимо друг от друга насаже­ны шестерня 1 и кривошип АВ длиной 30 см (рис. 113). На оси В кривошипа установлена шестерня 2 радиуса r₁ = 15 см, к которой прикреплен шатун 3. Определить угловую скорость шес­терни 1, когда угол φ = 90° и скорость v_С точки С ползуна равна 0,3 м/с. (2)

1.4.58. Ползуны 1 и 2, соединенные шарнирами А и В с шатуном 3 (114), движутся по неподвижным направляющим. Определить угловую скорость шатуна в момент, когда скорость точки А рав­на 0,2 м/с, если длины АС = ДС= 0,2 м. (1,0)

1.4.6. Ускорения точек плоской фигуры

Ускорения двух любых точек плоской фигуры А и В связаны между собой соотношением

, (48)

где - нормальное (центростремительное) ускорение

точки В - направ­лено от В к А по линии ВА и

; (49)

ω - мгновенная угловая скорость плоской фигуры;

- касательное (вращательное) ускорение точки В по отношению к точке А, оно перпендикулярно ВА и направлено в сторону вра­щения фигуры, если это вращение ускоренное, и в обрат­ную сторону, если оно замедленное.

Модуль этого ускорения определяют по формуле

,

где ε - мгновенное угловое ускорение плоской фигуры. Если известен мгновенный центр ускорений, т. е. точ­ка Q, ускорение которой в данный момент равно нуль-вектору, то ускорение любой точки А находят по формуле

, (50)

причем

. (51)

Если в некоторый момент известно ускорение точки А, а также величины ω и β, то для нахождения Q следует повернуть вектор в направлении вращения фигуры, если оно ускоренное (и в обратном - если замедленное), на острый угол α, определяемый формулой

. (52)

На полученной полупрямой следует отложить отрезок

. (53)

Конец Q этого отрезка и будет мгновенным центром уско­рений в данный момент.

Пример 2. Центр колеса, которое катится по наклонной плоскости без скольжения (рис. 115), движется по закону s = 4t² + 16 (t - в секундах, s - в сантиметрах). Определить ускорение точки касания колеса с плоско­стью в момент t = 2с, если радиус колеса R = 16 см.

Решение. Так как центр колеса О движется прямоли-нейно, то его модули скорости и ускорения находят по формулам

.

При t = 2с v₀ = 16 см/с; a₀ = 8 см/с².

Рис. 115

Ввиду отсутствия скольжения мгновенный центр скоростей нахо­дится в точке касания колеса с плоскостью. Следовательно, мгновен­ную угловую скорость ω получим по формуле

ω = v₀ /OP = t /2,

т. е. она представляет собой известную функцию времени. Дифферен­цируя по времени ω, найдем

.

И так, в рассматриваемый момент ω = 1 рад/с, ε = ½ рад/с².

Определим ускорение точки Р. По формуле (48);

,

где

= ω²OP = 16 см/с²,

причем направлено от Р к О, a = ε · OP = 8 см/с².

Так как колесо вращается ускоренно (ε и ω одного знака), то вращательное ускорение направлено перпендикулярно РО в сто­рону вращения фигуры вокруг полюса О.

В данном случае =0, следовательно, , а_р = 16 см/с². Вектор направлен к центру колеса О.

Задачи

1.4.59.* - 1.4.66.* С шатуном АВ кривошипно-ползунного механизма жестко связан треугольник ABD (рис. 116).. Определить модули ускорений точек В и D, если криво­шип ОА вращается с постоянной угловой скоростью ω. Данные взять из таблицы; принять ОА=АВ = а.

Рис. 116

№ задачи	ABD, град	BAD, град	φ, град
1.4.59	45	45	0
1.4.60	30	90	30
1.4.61	45	45	45
1.4.62	60	90	60
1.4.63	30	90	0
1.4.64	60	60	30
1.4.65	90	45	45
1.4.66	60	60	60

Ответы:

№ задачи
1.4.59
1.4.60
1.4.61
1.4.62
1.4.63
1.4.64
1.4.65
1.4.66

1.4.67.* Диск движется в своей плоскости так, что его центр О описывает окружность радиусом R с по­стоянной по модулю скоростью и вращается вокруг своего центра с постоянной угловой скоростью ω₀. Найти положение мгновенного центра ускорений диска.

Ответ: Мгновенный центр ускорений Q находится на прямой, соединяющей центры окружности и диска, при­чем

1.4.68.* В условиях предыдущей задачи центр диска имеет в данный момент то же значение скорости и об­ладает касательным ускорением . Какое угловое уско­рение ε надо сообщить диску (при прежней угловой ско­рости ω₀), чтобы мгновенный центр ускорений Q находился на прямой, соединяющей центры окружности и диска? На каком расстоянии от центра диска О будет при этом находиться мгновенный центр ускорений?

Ответ: . При ускоренном движении центра диск должен вращаться ускоренно в ту же сторону, в ко­торую движется центр, или замедленно в обратную сторону. При замедленном движении центра - все наоборот. Расстояние (сравните с ответом предыдущей задачи).

1.4.69.* Колесо радиусом R катится без скольже­ния по прямолинейному рельсу, имея в данный момент скорость центра (и произвольную величину ускорения центра). Определить модуль нормального ускорения точки на ободе колеса в зависимости от центрального угла ψ между радиусами, проведенными в данную точку и точку касания.

Ответ: .

1.4.70.* Колесо радиусом R катится без сколь­жения по неподвижному рельсу. Зная, что ускорение точки касания в данный момент равно , определить в этот момент модуль скорости диаметрально противоположной точки.

Ответ: v = 2 .

1.4.71.* Сум­мирующий механизм (рис. 117) состоит из зубчатого колеса радиу­сом r и двух параллельных зубчатых реек, движущихся в одном направлении с п остоянными скоростями и . Определить модули уско­рений точек A₁ и A₂ зубчатого колеса, находящихся в местах зацепления с рейкой.

Ответ: .

Рис. 117

1.4.72.* Решить задачу 1.4.71, считая, что рейки движутся в противоположных направлениях.

Ответ: .

1.4.73.* Решить задачу 1.4.71, считая, что рейки движутся в одну сторону, имея в данный момент скорости и и ускорения и соответственно.

Ответ: .

1.4.74.* Доказать, что центры кривизны траекто­рий различных точек обода колеса, катящегося без сколь­жения по прямолинейному рельсу, расположены симметрично этим точкам относительно точки касания колеса с рельсом.

1.4.75. Центр катящегося по плоскости колеса радиуса 0,5 м движется согласно уравнению s = 2t. Определить ускорение точки соприкос­новения колеса с плоскостью. (8)

1.4.76. Стержень АВ длиной 2 м находится в плос­копараллельном движении (рис. 118). Найти ускорение точки В, если ускорение точки А равно 1 м/с², угловая скорость стержня ω =1 рад/с, угло­вое ускорение ε = 0. (3)

1.4.77. Стержень АВ движется в плоскости (рис. 119). Уско­рение точки А в данный момент времени а_А = 1 м/с², угловая скорость ω = 2 рад/с, угло­вое ускорение ε = 2 рад/с². Определить уско­рение точки В стержня, если длина АВ = 1 м. (5)

1 .4.78. Тело находится в плоскопараллельном движении (рис. 120). Найти ускорение точки В, если ус­корение точки А равно 3 м/с², угловая ско­рость ω = 1 рад/с, угловое ускорение ε = О, расстояние АВ = 0,5 м. (2,5)

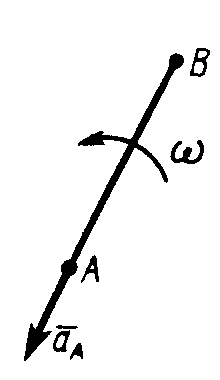
Рис. 118 Рис. 119 Рис. 120 Рис. 121

1.4.79. Колесо катится без скольжения (рис. 121). Опреде­лить ускорение точки В колеса в тот момент, когда скорость точки А равна нулю, а ускоре­ние а_А =2 м/с². (2,83)

1 .4.80. Колесо радиуса r = 0,1 м катится без скольжения (рис. 122). Определить ускорение точки В, если центр колеса А перемещается с по­стоянной скоростью v_A =2 м/с. (40)

Рис. 122 Рис. 123 Рис. 124

1.4.81. Скорость центра С колеса (рис. 123), катящего- ся бед скольжения, постоянна. Какой угол в градусах с осью Ох составляет вектор ускорения точки являющейся мгновенным центром скоростей колеса? (90)

1.4.82. Барабан 1 (рис. 124) вращается по закону φ = 0,1 t² . Определить ускорение груза 2, если радиус r = 0,2 м. (0,02)

Рис. 125 Рис. 126 Рис. 127

1.4.83. Кривошип ОА (рис. 125) вращается согласно закону ω = 0,5t. Определить ускорение точки М под­вижного колеса, если радиус R = 2 r = 0,2 м. (0,05)

1.4.84. Кривошип планетарного механизма (рис.126) вра­щается с постоянной угловой скоростью ω= 1 рад/с. Определить ускорение точки, явля­ющейся мгновенным центром скоростей под­вижного колеса, если радиус R = 0,1 м. (0,2)

1.4.85. Стержень длиной АВ = 40 см движется в плоскости чертежа (рис. 127). В некоторый момент времени точки А и В стержня имеют ускорения а_А = 2 м/с² и а_В = 6 м/с². Определить угловое ускорение стержня. (10)

1.4.86. Тело находится в плоскопараллельном движении (рис. 128). Найти его угловую скорость, если ускорение точки А равно 1 м/с², ускорение точки В равно 6 м/с², расстояние АВ = 1 м, угол α = 60°. (2)

1.4.87. Квадратная пластина ABDE движется в плоскости Оху (рис. 129). Определить угловое ускорение пластины в указанном положении, если длина АВ = 0,5 м, а проекции ускорений точек А и В на ось Оу с оответственно равны а_Ау = 3 м/с², а_Ву=6 м/с². (4)

Рис. 128 Рис. 129 Рис. 130

1.4.88. Стержень АВ длиной 50 см движется в плоскости чертежа (рис. 130). В некоторый момент вре­мени точки А и В стержня имеют ускорения а_А= 2 м/с², а_В = 3 м/с². Определить угловое ускорение стержня. (10)

1.4.89. Кривошип ОА (рис. 131) равномерно вращается с угловой скоростью

ω = 10 рад/с. Определить угловое ускорение шатуна АВ, если в данный момент времени механизм занимает положе­ние, показанное на рисунке. (0)

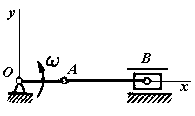
Рис. 131 Рис. 132

1.4.90. Определить ускорение ползуна В кривошипно-ползунного механизма (рис.132) в данном поло­жении, если угловая скорость кривошипа ω = 1 рад/с = const; длины звеньев ОА = 0,3 м; АВ = 0,5 м. (0,225)

1.4.91. В указанном на рисунке 133 положении шарнирного четырехзвенника скорость и ускорение точки А кривошипа ОА равны: v_А = 2 м/с, а_А = 20 м/с². Определить ускорение точки В шатуна АВ, если длины А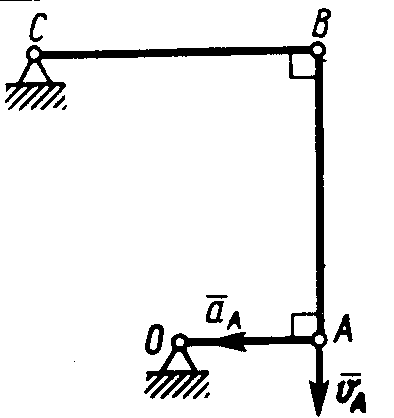 В = ВС = 0,8 м. (25)

Рис .133 Рис. 134

1 .4.92. В указанном на рисунке 134 положении шарнирного четырехзвенника скорость и ускорение точки А кривошипа ОА равны: v_A = 2 м/с, а_B = 40 м/с². Определить угловое ускорение звена ВС, если длины звеньев АВ = ВС = 0 5 м. (0)

Рис. 135 Рис. 136

1.4.93. Определить угловое ускорение шатуна АВ кривошипно-ползунного механизма в данном положении (рис. 135), если кривошип ОА вращается с постоянной угловой скоростью ω = 10 рад/с, а длины звеньев ОА = 0,3 м, АВ = 0,45 м. (94,3)

1.4.94. Кривошип ОА шарнирного параллелограм­ма ОАВО₁ (рис. 136) равномерно вращается с угловой скоростью ω= 4 рад/с. Определить угловое ускорение ш атуна, CD в данном положении механизма, если длины звеньев ОА = 20 см, СО =30 см. (12,3)

1.4.95. Для данного положения механизма (рис.137) опре­делить ускорение ползуна В, если колесо радиуса R = 50 см катится с постоянной ско­ростью его центра v₀ = 5 м/с;

Рис. 137 угол α = 30°. (28,9)