Применение средств Поиск решения ms Excel для решения задач линейного программирования.
Пример 1.
Компания может выпускать два вида изделий Р1 и Р2. Для их изготовления используются три вида ресурсов R1, R2, R3. Известны нормы расхода ресурсов на единицу продукции каждого вида:
-
Ресурсы
Продукты
Р1
Р2.
R1
1
2
R2
1
1
R3
3
1
Известны также цены ресурсов (за единицу) и возможные объемы поставок ресурсов в течение месяца:
-
Ресурсы
цена
допустимый объем.
R1
$10
200
R2
$10
150
R3
$40
390
На рынке сложились цены, по которым может быть продано любое количество изделий каждого вида. Цена изделия первого вида составляет $170, второго – $120. Рассмотрим задачу нахождения плана, который обеспечит получение максимального объема реализованной продукции.
Для построения формальной модели введем переменные:
Х1 – объем выпуска (количество) изделий первого вида
Х2 - объем выпуска (количество) изделий второго вида
Поскольку введенные переменные обозначают объемы выпуска продукции, они должны подчиняться условию неотрицательности: X1,X2 ³0.
С помощью введенных переменных мы можем записать ограничения по объемам доступных ресурсов:
1* Х1 + 2* Х2 £ 200
1* Х1 + 1* Х2 £ 150
3* Х1 + 1* Х2 £ 390
Целевая функция (общий объем продаж) может быть представлена с помощью введенных переменных следующим образом:
Z = 170* Х1 + 120* Х2
Решение задачи линейного программирования с помощью средств Поиск решения ms Excel.
Рассмотрим основные этапы процесса решения задачи линейного программирования с помощью Excel на примере задачи об оптимальном плане выпуска продукции (условие задачи представлено в примере 1).
Этап 1. Организуйте данные на листе MS Excel так, как это показано на рисунке 1.
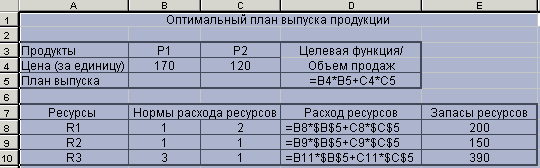
Рисунок 1. Постановка задачи нахождения оптимального плана выпуска продукции.
В ячейках В5 и С5 будут расположены искомые значения переменных Х1 и Х2.
В ячейку D5 введена формула, которая позволяет вычислять значение целевой функции Z=170*X1+120*X2 (представляющей общий объем реализованной продукции) при продаже X1 изделий первого вида и X2 изделий второго вида.
В ячейки D8, D9, D10 - введены формулы, отражающие общий расход ресурсов R1, R2, R3 при выпуске X1 изделий первого вида и X2 - изделий второго вида.
R1 1* Х1 + 2* Х2
R2 1* Х1 + 1* Х2
R3 3* Х1 + 1* Х2
Этап 2. Выберите пункт меню Сервис – Поиск Решения. Появится окно Поиск решения (Рисунок 2).
В поле окна “Установить целевую ячейку” отметьте ячейку D5 (щелкните сначала по полю окна, а затем по ячейке D5)
Установите флажок на отметке “Равной максимальному значению”
В поле окна “Изменяя ячейки” отметьте ячейки В5 и С5
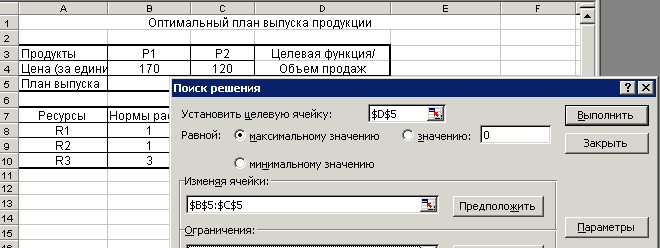
Рисунок 2. Задание целевой ячейки и изменяемых ячеек.
Этап 3. Введите последовательно все ограничения, щелкая по кнопке “Добавить” (как показано на рисунках 3 и 4)
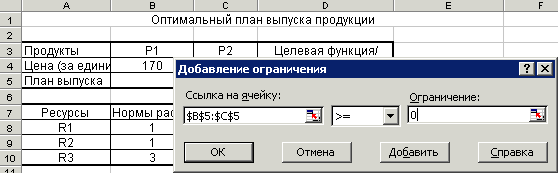
Рисунок 3. Введение условий неотрицательности переменных.
В появившемся окне щелкните в поле “Ссылка на ячейку”, а затем отметьте ячейки B5:C5, выберите знак ограничения ³, щелкните на правое поле “Ограничение” и введите в него значение 0. Таким образом Вы ввели ограничения: X1,X2 ³0.
Рисунок 4. Введение ограничений по объемам ресурсов.
Вновь щелкните на кнопке “Добавить”. В появившемся окне щелкните в поле “Ссылка на ячейку”, а затем отметьте ячейку D8, выберите знак ограничения £, щелкните на правое поле “Ограничение” и отметьте в нем ячейку E8, содержащую ограничение на доступный объем ресурса R 1. Таким образом, Вы ввели ограничение 1*X1+2*X2 £ 200.
Продолжайте процесс и введите ограничения по объемам ресурсов R2, R3.
Этап 4. Нахождение оптимального решения.
После того, как введены все ограничения, следует щелкнуть на кнопке «Параметры» и в открывшемся окне установить флажок «Линейная модель», для получения решения достаточно щелкнуть на кнопке “Выполнить” Полученное решение представлено на рисунке 5.
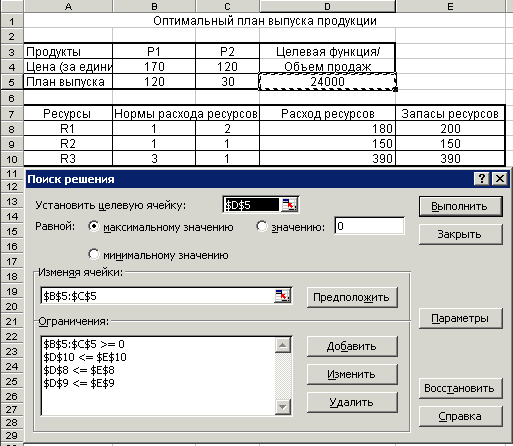
Рисунок 5. Оптимальный план выпуска.
В ячейке D5 приведено оптимальное значение целевой функции. При соблюдении всех ограничений максимальный объем продаж может составить 24000. Оптимальные объемы выпуска изделий первого и второго вида указаны в ячейках B5:C5 :X1 =120, X2 = 30.
В ячейках D8, D9, D10 содержатся объемы ресурсов, которые будут необходимы для реализации найденного оптимального плана. При этом можно заметить, что ресурсы второго и третьего вида будут израсходованы полностью, а для ресурса первого вида останется неиспользованный запас (избыток) в 20 единиц.