Транспортная задача линейного программирования
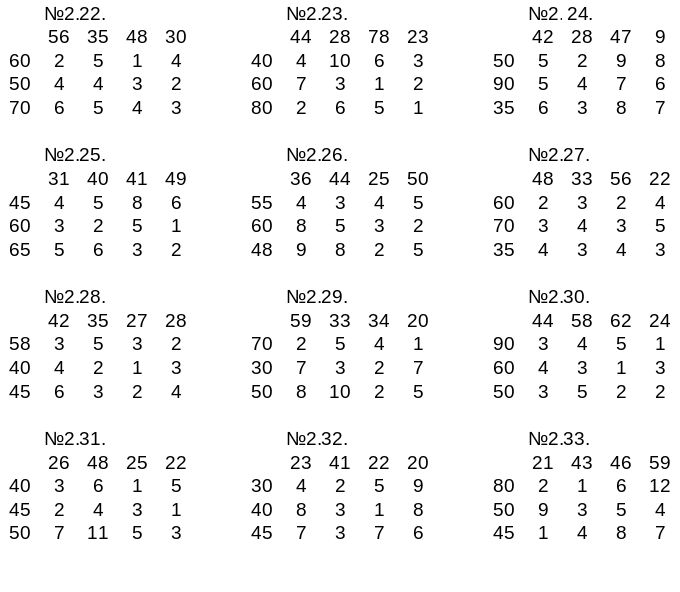
Приложение 3
Нелинейная задача распределения ресурсов. Динамическое программирование
№3.1.
хj |
0 100 200 300 400 500 600 700 |
f1 (xj) |
0 20 44 55 63 67 70 70 |
f2 (xj) |
0 18 29 49 72 87 100 108 |
f3 (xj) |
0 25 41 52 74 82 88 90 |
f4 (xj) |
0 30 52 76 90 104 116 125 |
Приложение 4
Динамическая задача управления производством и запасами
-
d1
d2
d3
a
b
c
h1
h2
h3
y1
№ 4.1
5
6
7
2
3
4
4
3
2
2
№ 4.2
3
2
3
1
2
2
4
3
2
3
№ 4.3
5
2
3
2
2
2
4
5
6
4
-
№ 4.4
2
3
3
2
3
4
3
2
2
2
№ 4.5
3
2
3
1
3
2
4
3
2
1
№ 4.6
3
2
4
5
1
0
3
3
3
2
-
№ 4.7
3
2
4
8
1
1
1
0
1
0
№ 4.8
6
2
4
3
4
3
2
1
3
1
№ 4.9
5
4
3
4
4
4
5
0
4
2
-
№ 4.10
7
3
4
2
1
3
2
5
7
4
№ 4.11
3
3
4
2
3
4
2
3
1
3
№ 4.12
3
2
3
2
2
1
2
3
4
3
-
№ 4.13
1
2
3
2
3
1
1
2
3
1
№ 4.14
2
3
2
5
1
1
3
2
1
2
№ 4.15
4
2
2
1
1
2
6
4
1
0
-
№ 4.16
7
0
4
3
4
0
3
3
3
2
№ 4.17
2
2
2
1
1
5
1
2
4
2
№ 4.18
5
1
2
2
0
6
2
1
1
4
-
№ 4.19
3
1
2
4
1
2
6
3
5
0
№ 4.20
6
0
3
1
3
3
5
3
1
4
№ 4.21
4
5
2
3
3
3
4
0
5
2
-
№ 4.22
4
5
1
5
0
2
4
7
0
4
№ 4.23
5
3
1
2
4
3
5
4
3
1
№ 4.24
6
2
1
4
0
5
3
4
1
5
-
№ 4.25
3
2
1
4
5
0
5
4
0
2
№ 4.26
7
6
0
1
0
5
4
5
3
4
№ 4.27
5
5
2
1
0
1
3
4
4
4
-
№ 4.28
4
5
2
5
0
4
4
4
4
4
№ 4.29
6
5
1
4
1
1
3
7
0
3
№ 4.30
4
3
3
4
3
2
1
3
2
3
-
№ 4.31
6
5
1
2
4
1
4
4
4
4
№ 4.32
3
0
4
4
4
4
1
3
4
3
№ 4.33
5
0
4
7
0
4
1
1
1
2
Приложение 5