Функция Грина для круга

Функция Грина (источника) для круга может быть получена таким же способом, как и функция для сферы. В этом случае функцию следует искать в виде

.

Повторяя рассуждения предыдущего пункта, мы найдем функцию G в виде:

,

где , , , 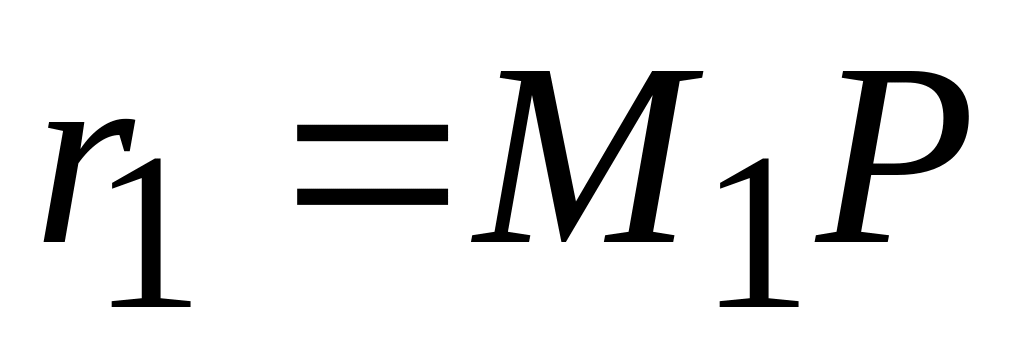- радиус круга (рис. 11). Нетрудно убедиться в том, что определенная таким образом гармоническая функция обращается в нуль на границе .

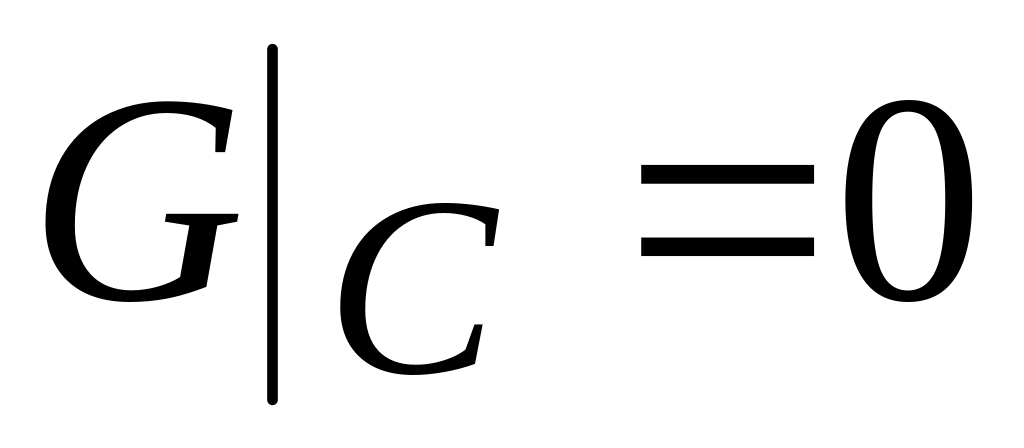P r₁ M₁

r

R ₁

M₀



O

Рис. 11

Для решения первой краевой задачи надо вычислить значения 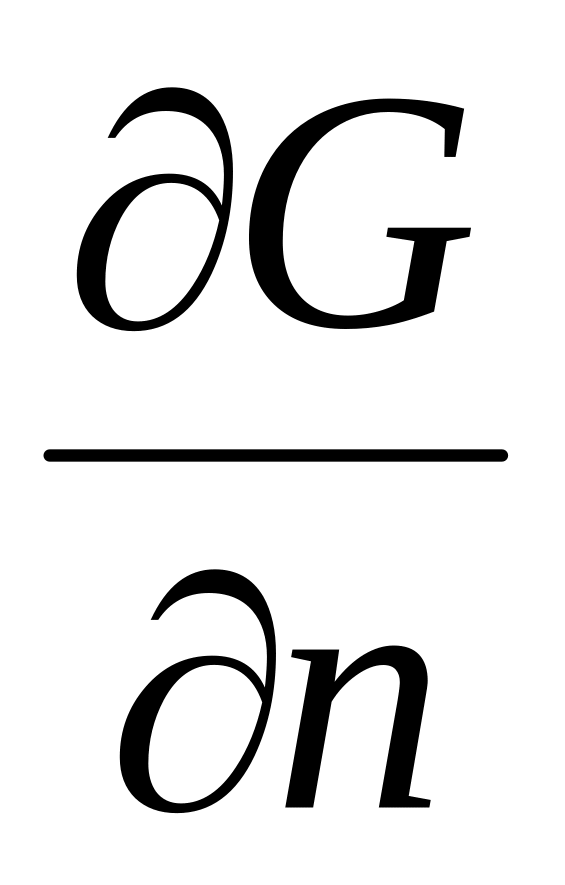на окружности C. Вычисления проходят аналогично случаю сферы и дают:

.

Пусть - полярные координаты точки P, лежащей на окружности, а ( - координаты точки , тогда

.

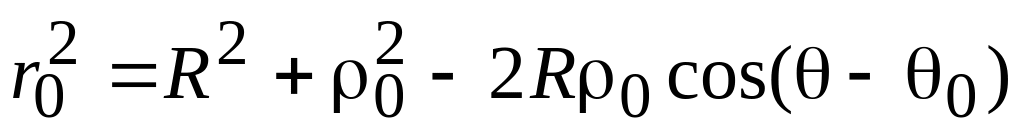Подставляя в формулу

это выражение для 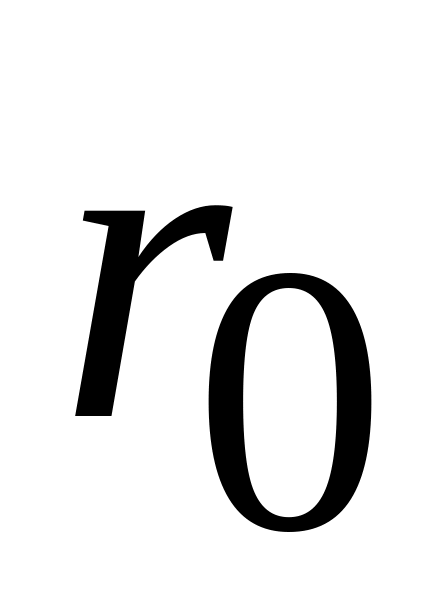и принимая во внимание, что

и ,

приходим для функции к выражению

,

называемому интегралом Пуассона для круга.