2.3.2. Метод Блейка

Напомним операцию обобщенного склеивания:

 =   .

Конъюнкцию будем называть результатом обобщенного склеивания. Именно среди результатов обобщенного склеивания, многократно примененного к конъюнкциям произвольной ДНФ булевой функции f( ,…, ), оказываются простые импликанты булевой функции.

Теорема 2.5 (теорема Блейка). Сокращенная ДНФ функции f( ,…, ) получается из произвольной ДНФ этой функции путем выполнения всевозможных операций обобщенного склеивания и поглощения конъюнкций.

Доказательство приведено в работе [Диск.мат. 74].

Изложим на основе теоремы алгоритм Блейка. Пусть предварительно в заданной ДНФ выполнены всевозможные поглощения конъюнкций.

Алгоритм.

1. Начиная со второй конъюнкции в ДНФ D, выбираем очередную конъюнкцию и пытаемся выполнить для нее операцию простого склеивания с предшествующими конъюнкциями D, с первой, второй и т.д. по порядку. Пусть операция склеивания с конъюнкцией , j < i, выполнима и k – результат обобщенного склеивания. Тогда возможны следующие ситуации:

• k поглощается одной из конъюнкций D, переходим к п. 2 алгоритма,

• иначе приписываем конъюнкцию k справа к D, исключив из D все конъюнкции, поглощаемые k.

Обозначаем полученную ДНФ также через D и переходим к п. 2 алгоритма.

2. Продолжаем просмотр предшествующих для конъюнкций из D. Если все предшествующие конъюнкции просмотрены, увеличиваем i на единицу, если это возможно, и переходим к п. 1 алгоритма. Если все конъюнкции просмотрены, переходим к п. 3.

3. Очередная ДНФ D представляет сокращенную ДНФ булевой функции f( ,…, ).

Проиллюстрируем применение алгоритма Блейка на примере. Имеем ДНФ:   .

Выполнив операцию обобщенного склеивания второй и первой конъюнкций с последующим поглощением конъюнкцией xy первой конъюнкции, получим:   .

Выполнив операцию обобщенного склеивания второй и первой конъюнкций, полученной на предыдущем шаге ДНФ, имеем:    .

Выполнив операцию обобщенного склеивания третьей и второй конъюнкций с последующим поглощением конъюнкцией y второй, третьей, четвертой конъюнкций, получим сокращенную ДНФ: xz  y.

Будем иметь в виду, что если мы хотим получить из построенной методом Блейка сокращенной ДНФ все минимальные или все кратчайшие ДНФ, нам придется извлекать совершенную ДНФ, чтобы воспользоваться таблицей Квайна.

Если ДНФ представляет константу 1, то в процессе реализации всевозможных простых склеиваний эта константа будет получена. Заметим, что применение алгоритма Блейка для проверки ДНФ на представление ею константы 1, как правило, неэффективно в смысле требуемых вычислительных затрат.

КАДР

2.4. Получение безызбыточных (тупиковых) днф

Имея сокращенную ДНФ, можно пытаться выбрасывать из нее некоторые конъюнкции, чтобы получать безызбыточные (тупиковые) ДНФ, состоящие, например, из конъюнкций по возможности меньших рангов. Такие безызбыточные ДНФ могут оказаться достаточно близкими к кратчайшим ДНФ, и для их получения не требуется иметь все безызбыточные ДНФ. При этом подходе к получению безызбыточных ДНФ необходимо уметь находить конъюнкции, которые можно исключить из заданной ДНФ, не важно, какой именно: сокращенной или произвольной.

Удаляемая конъюнкция должна удовлетворять условию: представляющий ее интервал содержится в объединении интервалов оставшихся конъюнкций заданной ДНФ:

.

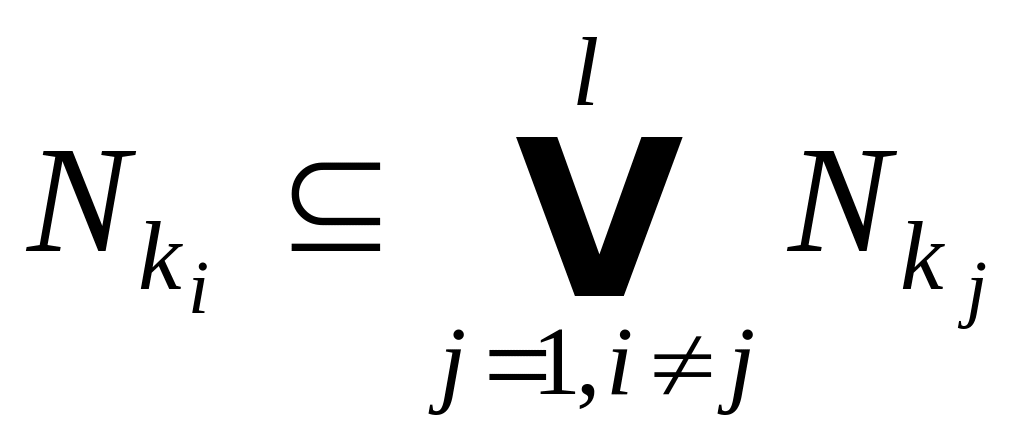Иными словами, конъюнкция поглощается оставшимися конъюнкциями рассматриваемой ДНФ. Речь идет о совместном поглощении конъюнкции .

Можно перейти к следующей постановке задачи. Имеем произвольную конъюнкцию k, не принадлежащую рассматриваемой ДНФ D, необходимо выяснить, не поглощается ли она этой ДНФ. Нас интересует ситуация, когда отдельная конъюнкция ДНФ не поглощает конъюнкцию k.

Определение. Конъюнкции , будем называть ортогональными, если сопоставляемые им интервалы имеют пустое пересечение: .

В ортогональных конъюнкциях найдется хотя бы одна переменная, такая, что в одной из конъюнкций эта переменная присутствует с инверсией, а в другой – без инверсии.

Например, конъюнкции , ортогональны по переменной .

Очевидно, что конъюнкции ДНФ D, ортогональные конъюнкции k, не могут участвовать в совместном поглощении конъюнкции k, поэтому исключим их все из ДНФ D. Полученную ДНФ обозначим . Задачу сведем к проверке поглощения конъюнкции k ДНФ .

Выполним разложение ДНФ по конъюнкции k следующим образом. Каждую конъюнкцию из представим в виде произведения , включая в первый сомножитель буквы, присутствующие в k и одновременно. Если таких букв нет, сомножитель равен 1. В включаются остальные буквы конъюнкции .

Итак, = .

КАДР

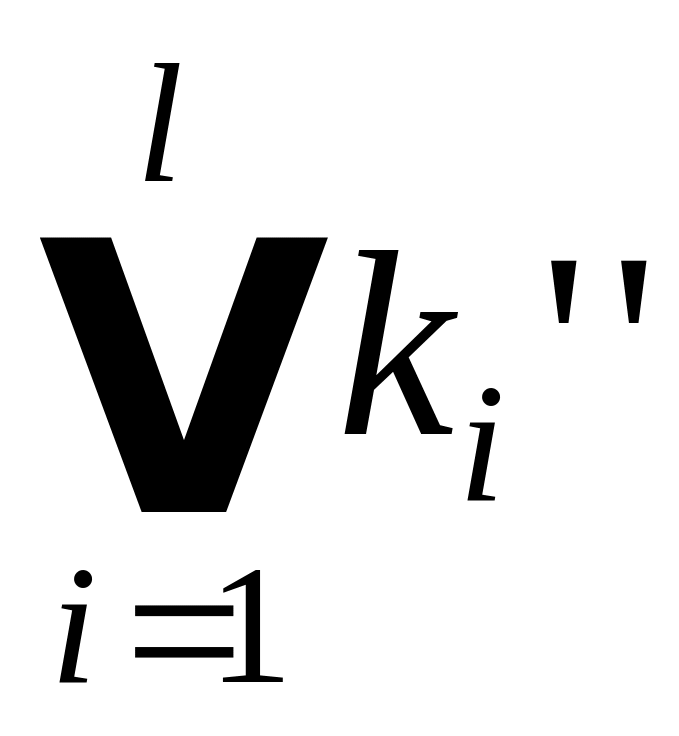
Теорема 2.6. k , если и только если  1.

Доказательство. Достаточность. Пусть условие теоремы выполняется. Покажем, что k . Для этого рассмотрим произвольный набор α значений переменных ДНФ. Если k(α) = 0, то значение (α) нас не интересует. Пусть k(α) = 1,тогда по построению = 1 для любого i. Имеем

(α) = = 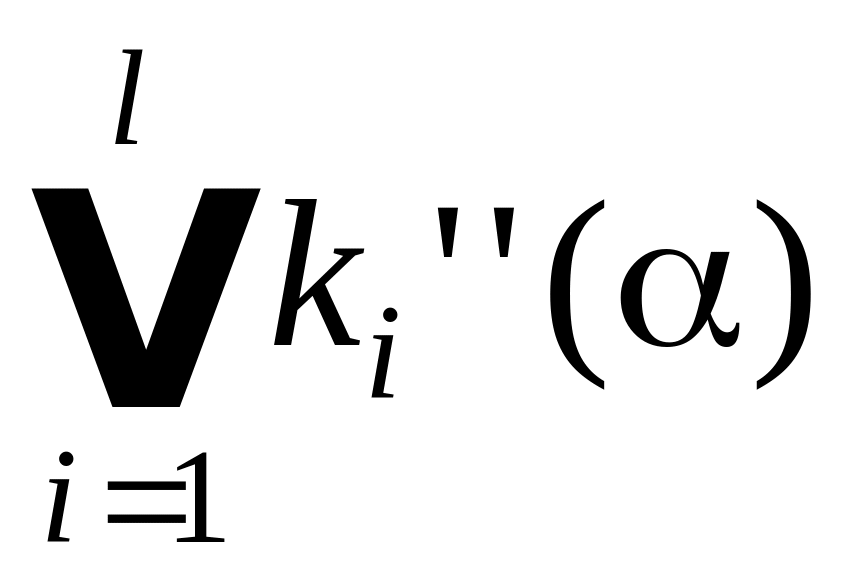, но  1 из условия теоремы. Следовательно, (α) = 1. Поскольку α – произвольный набор, на котором k(α) = 1, k .

Необходимость. Пусть k . Рассмотрим произвольный набор α. Возможны две ситуации:

1. Пусть k(α) = 1, тогда (α) = 1 и (α) = 1. При любом i имеем

1 = (α) = =  1.

2. Пусть k(α) = 0. Изменим набор α на набор β, так что k(β) = 1, и β отличается от α только по переменным, присутствующим в конъюнкции k, тогда имеем

= 1.

По построению не содержит переменных, общих с конъюнкцией k. Следовательно,  1. Ч.Т.Д.

Проиллюстрируем применение теоремы примером. Имеем сокращенную ДНФ:

  xz  xy   .

Выделим конъюнкцию и построим для нее ДНФ =  xz. Воспользуемся теоремой 2.6, получим из выражение  x = 1. Следовательно, выделенная конъюнкция поглощается оставшимися конъюнкциями исходной ДНФ и может быть из исходной ДНФ удалена. После удаления конъюнкции имеем ДНФ :

=  xz  xy   .

Рассуждая аналогичным образом, получим, что конъюнкция может быть удалена из . В результате имеем безызбыточную (тупиковую) ДНФ :

=  xz  xy  ,

из которой ни одна из конъюнкций не может быть удалена.

Возьмем, например, конъюнкцию xz. Для нее = xy. Исключив из переменные конъюнкции xz, получим y. Эта функция не равна константе 1, поскольку обращается в единицу на одном из двух наборов представляющей ее таблицы истинности, и т.д.

ДНФ можно рассматривать не только как формулу, но и как множество составляющих ее конъюнкций. Тогда можно говорить о пересечении и объединении ДНФ. Операции объединения и пересечения ДНФ обычно выполняют либо над множествами конъюнкций, представляющих безызбыточные (тупиковые) ДНФ, либо над множествами конъюнкций, представляющих минимальные ДНФ.

Рассмотрим сокращенную ДНФ:

D =      .

Пронумеруем конъюнкции этой ДНФ слева направо. Из нее можно получить две тупиковые ДНФ:

=    ,

=    .

Образуем пересечение тупиковых ДНФ:

=   ,

а затем их объединение:

=     .

КАДР