1.3. Действия над событиями

Введем основные операции над событиями, по аналогии операциями над множествами.

ОПР. Суммой событий А и В называемся событие С= А+В, состоящие в наступлении хотя бы одного из этих событий (т.е. или А , или В, или А и В вместе)

ОПР. Произведением событий А и В называемся событие С =А*В, состоящее в совместном наступлении всех этих событий (т.е. А и В одновременно).

ОПР. Разностью событий А и В называется событие С = А-В, наступающее тогда и только, когда наступит событие А. но не наступает событие В.

ОПР. Противоположным событию А называется событие Ā, которое происходит тогда и только тогда, когда не происходит событие А (т.е. событие А не наступило).

ОПР. Два несовместных события, образующие полную группу, называются и противоположными. (Ā - противоположное событию А)

ОПР. Событие А влечет событие В (т.е. А является частным случаем В), если из того, что происходит событие А, следует, что происходит событие В.( )

ОПР. Если и , то События А и В называют равными.

События и действия над ними наглядно иллюстрируют диаграммы Эйлера – Венна :достоверное событие изображают прямоугольником; элементарные события – точками прямоугольника; случайные события – областью внутри него.(рис.)

A+B, А*В А-В

Операции над событиями обладают следующими свойствами:

• А+В=В+А, А∙В = В∙А (переместительный)

• А(В+С)=А∙В+А∙С; А∙В +С= (А+С)∙(В+С) (распределительный)

• А+(В+С)=(А+В)+С; (АВ)С=А(ВС) (сочетательный)

• А+А=А; А*А=А;

• А+ = ; А* = А;

• А+Ā= ; А*Ā= ;

• = ; ;

• ; - законы де Моргана.

1.4. Случайные события. Алгебра событий.

Определим основные понятия ТВ по теоретико – множественному подходу Колмогорова А.Н. в 1933г.

Пусть производятся некоторые опыты со случайным исходом.

ОПР. Множество всех взаимоисключающих исходов опыта называется пространством элементарных событий.(ПЭС), а сами исходы - элементарными событиями.

ОРП. Случайным событием А(или просто событием) называют любое подмножества множества , если оно конечно или счетно (т.е. элементы множества можно пронумеровать с помощью множества натуральных чисел) .Элементарные события, входящие в подмножество А пространства , называются благоприятствующими событию А.

ОРП. Множество называется достоверным событием. Ему благоприятствует любое элементарное событие, которое обязательно произойдет в данном опыте. Пустое множество  называется невозможным событием.

Пр.4. Опыт - 1раз бросаем игральную костью.

В этом случае ПЭС таково: или , где - элементарное событие, состоящее в выпадении i-ой грани с i очками. В данном случае - конечное множество.

Примером события А является, например, выпадение числа очков кратных 3,т.е. , т.е. событию А благоприятствуют элементарные события .

ПР.5. Опыт – стрельба по цели до первого попадания.

, где П – попадание в цель, Н - промах. Исходов теоретически в этом опыте бесконечно.

ПР.6. Опыт – наблюдение за временем безотказной работы некоторого агрегата.

В данном опыте можем получить любое ; время которое меняется непрерывно. ПЭС- , несчетно.

Над событиями проводят все операции множеств.

ОПР.1. Суммой или объединением двух событий и (обозначается А+В или )- это множество, которое содержит элементы, принадлежащие хотя бы одному из событий А и В.

2.Произведением двух событий двух событий и (обозначается АВ или )- это множество, которое содержит элементы, общие для событий А и В.

3.Разностью двух событий и (обозначается А-В или )- это множество, которое содержит элементы события А, не принадлежащие событию В.

4.Противоположное событию событие ( или дополнение множества А).

5.Событие А влечет событие В , если каждый элемент А содержится в В ( ).

ОПР. События А и В называются несовместными, если их произведение есть невозможное событие , в противном случае они совместны.

ОПР. Несколько событий образуют полную группу несовместных событий, если их сумма представляет всё ПЭС, а сами события несовместны, т.е. .

В случае несчетного пространства в качестве событий рассматриваются не все подмножества , а лишь некоторые классы этих подмножеств, называемые алгебрами и - алгебрами множеств.

ОПР. Класс S подмножеств пространства называется алгеброй событий (множеств), если:

1. ;

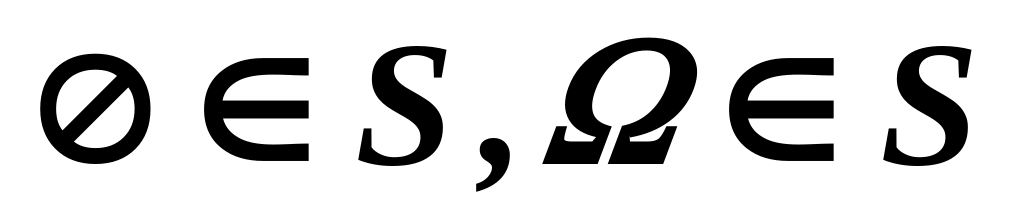2. из 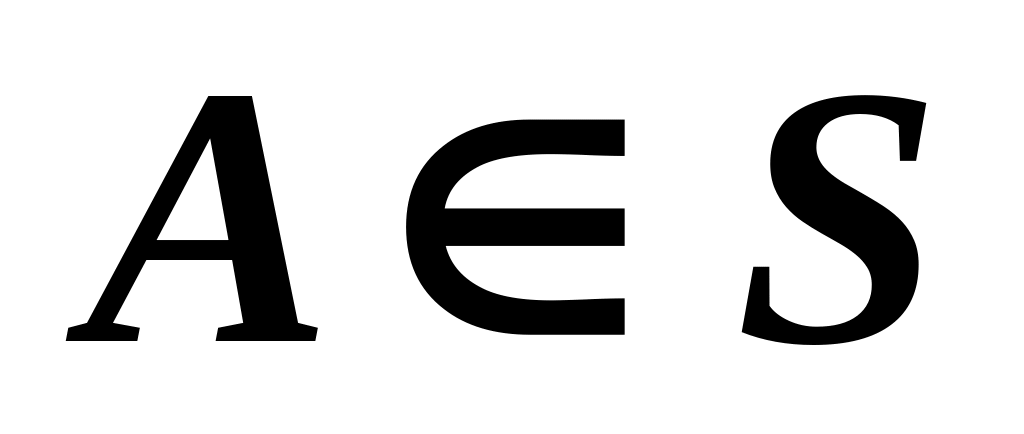вытекает, что ;

3. из вытекает, что

Заметим, что в условии 3 достаточно, требовать либо , либо , так как .

Алгебру событий образует, например, система подмножеств . Действительно, в результате применения любой из вышеприведенных операций к любым двум элементам класса S снова получается элемент данного класса: .

При расширении операций сложения и умножения на случай счетного множества S называется - алгеброй, если из следует .

Множество всех подмножеств множества , если оно конечно или счетно, образует алгебру.