Якобиан.

Пусть – -мерная вектор-функция переменных, дифференцируемая в точке . В данном случае производная матрица является квадратной, размера . Для такой матрицы может быть вычислен определитель. Этот определитель называется якобианом и обозначается .

Примеры. 1. Сосчитаем якобиан перехода от полярных координат к декартовым координатам. Напомним формулы: . Имеем .

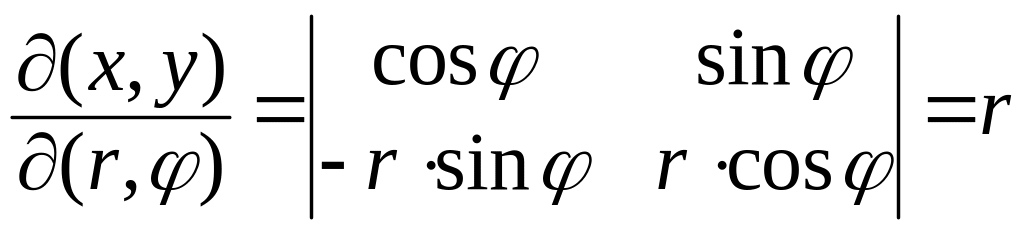2. Сосчитаем якобиан перехода от сферических координат к декартовым координатам. Напомним формулы:

. Имеем .

Касательная плоскость к поверхности, заданной параметрически.

Мы уже знаем, что касательная плоскость к поверхности, заданной явно в виде , в точке имеет уравнение .

Пусть теперь та же поверхность задана параметрически:

где – параметры, причем и .

В соответствии с явным и параметрическим заданиями одной и той же поверхности имеем . Это значит, что мы имеем суперпозицию функции двух переменных и вектор-функции . Поэтому производная матрица-строка равна произведению матрицы-строки на квадратную матрицу 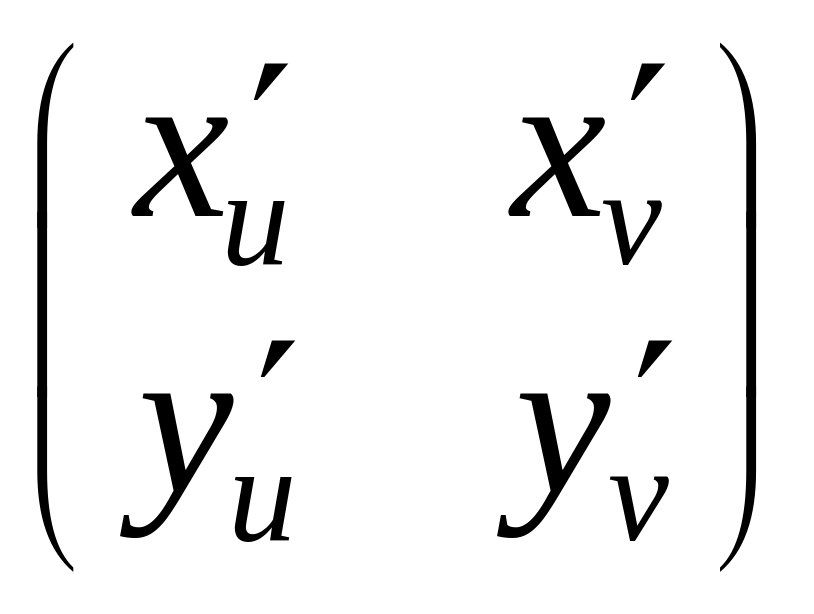. Сравнивая элементы одинаковых матриц, получим

Последние соотношения можно рассматривать как систему относительно и . Система с ненулевым главным определителем имеет единственное решение, которое можно найти с помощью правила Крамера: .

Подставляя полученные частные производные в уравнение касательной плоскости к поверхности, заданной в явном виде, получим уравнение касательной плоскости к поверхности, заданной параметрически:

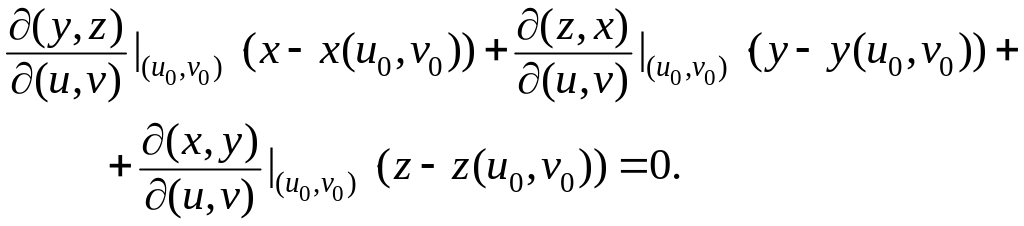
Производная по направлению.

1. Случай функции двух переменных . Направление задается вектором. Выберем единичный вектор, задающий направление на плоскости: . Этот вектор образует угол с положительным направлением оси OX. Производной функции двух переменных по направлению называется выражение .

2. Случай функции трех переменных . Пусть задан единичный вектор , образующий углы с осями OX, OY и OZ, соответственно. Если обозначить координаты вектора через , то по формуле косинуса угла между двумя векторами и получим . Аналогично, . Таким образом, единичный вектор, образующий углы с осями OX, OY и OZ, имеет координаты . Производной функции трех переменных по направлению называется выражение

.

Частные производные высших порядков.

Любая частная производная функции переменных сама также является функцией переменных. Частная производная от частной производной функции многих переменных называется частной производной второго порядка функции . При этом, если переменные, по которым берутся производные сначала от функции , а затем от функции , не совпадают, такая частная производная называется смешанной. Обозначения частной производной второго порядка: . В том случае, когда и – непрерывные функции в окрестности некоторой точки, в этой точке.

Аналогично вводятся частные производные любого порядка.

Дифференциалы высших порядков.

По аналогии с производными вводятся дифференциалы высших порядков, то есть дифференциалы от дифференциалов. Рассмотрим функцию трех переменных . Дифференциалом этой функции является выражение . Заметим, что входящие в последнее выражение производные – функции от , а дифференциалы переменных не зависят от . Поэтому при условии непрерывности смешанных производных дифференциал второго порядка имеет вид

.

В последней формуле мы воспользовались свойством равенства смешенных производных. Нетрудно видеть, что формула дифференциала второго порядка аналогична формуле второй степени суммы трех слагаемых. Нетрудно сосчитать дифференциалы второго и третьего порядков функции двух переменных : ,

.

Формула Тейлора для функции многих переменных.

Как и в случае функций одной переменной, для функций многих переменных формула Тейлора дает связь между приращением функции в точке и ее дифференциалами в этой же точке:

где .

В частности, для функции двух переменных имеем:

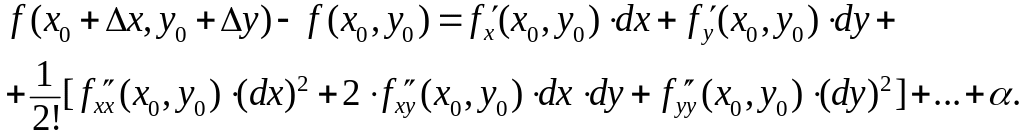
Здесь .

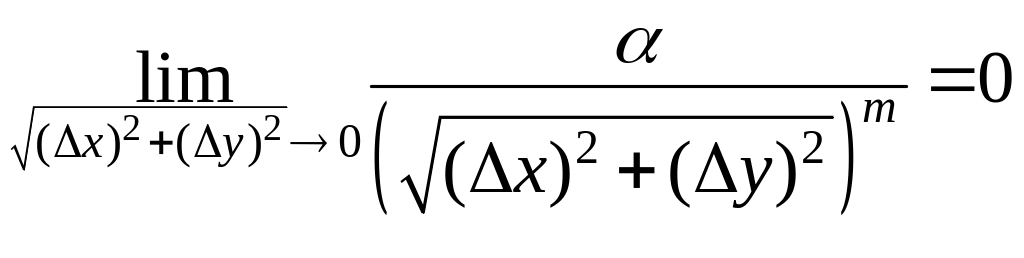Локальный экстремум функции многих переменных.

Точкой локального экстремума функции называется такая точка , для которой в области существует окрестность, в которой разность не меняет знак. В частности, точка является точкой минимума, если , и точка является точкой максимума, если .

Необходимое условие локального экстремума.

Пусть – точка экстремума, и функция дифференцируема в точке . Рассмотрим функцию одной переменной , где – любое натуральное число между 1 и . Эта функция имеет точкой экстремума точку , и значит, . Следовательно, необходимым условием экстремума функции многих переменных в точке , где она дифференцируема, является следующее условие: . Точка, в которой все частные производные первого порядка данной функции равны нулю, называется критической точкой этой функции.

Достаточное условие локального экстремума.

Выполнение необходимого условия экстремума не обязательно обеспечивает действительное наличие экстремума в точке, то есть, критическая точка функции может не быть точкой локального экстремума. В качестве примера рассмотрим функцию двух переменных . Критической точкой для этой функции является точка (0,0). Однако эта точка является не экстремальной, а седловой.

hypar.wxm

Для того чтобы выяснить, достигается ли в критической точке экстремум и какой, следует обратиться к дифференциалу второго порядка в этой точке. Итак, пусть – критическая точка для функции многих переменных . В этом случае . В соответствии с формулой Тейлора

где .

Поэтому знак разности в окрестности точки определяется знаком дифференциала второго порядка в точке при всевозможных малых приращениях .

Рассмотрим случай . Пусть критическая точка имеет координаты . Рассмотрим приращение функции в окрестности этой точки:

Если при любом сочетании бесконечно малых приращений выражение в квадратных скобках не меняет знак, то данная критическая точка является точкой локального экстремума. Вынесем за квадратную скобку множитель . Знак приращения функции совпадает со знаком квадратного трехчлена относительно . Как известно, квадратный трехчлен не меняет знак в том случае, если не имеет корней, то есть если его дискриминант отрицателен. В случае отрицательного дискриминанта знак квадратного трехчлена определяется знаком коэффициента при наибольшей степени (или знаком свободного члена). Таким образом, критическая точка с координатами является точкой локального экстремума, если . При этом мы имеем точку минимума, если , и точку максимума, если .