
- •Казанский государственный энергетический университет Кафедра «Высшей математики»
- •Тема : Функции комплексной переменной.
- •Вид уравнения Тип числа ____ Множество:
- •При перемножении и делении двух кч в тригонометрической форме
- •Используют тригонометрические формулы для суммы и разности двух углов и получают
- •Устные экзаменационные вопросы
При перемножении и делении двух кч в тригонометрической форме
z1
= r1
(
cos
![]() 1
+ i sin
1
+ i sin
![]() 1
) , z2
=
r2
(
cos
1
) , z2
=
r2
(
cos
![]() 2
+ i sin
2
+ i sin
![]() 2
)
2
)
Используют тригонометрические формулы для суммы и разности двух углов и получают
z1
z2
= r1
r2
( cos (![]() 1
+
1
+
![]() 2
)
+ i sin (
2
)
+ i sin (![]() 1
+
1
+
![]() 2
)
)
2
)
)
z1
/ z2
=
r1/
r2
(
cos (![]() 1
-
1
-
![]() 2
)
+ i sin (
2
)
+ i sin (![]() 1
-
1
-
![]() 2
)
)
2
)
)
z
n
=
[r
(
cos
![]() + i sin
+ i sin![]() )]n
= r n
(
cos n
)]n
= r n
(
cos n
![]() + i sin n
+ i sin n![]() )
)
![]() =
=
![]() [
cos (
[
cos (![]() +
2
+
2![]() k)/
n + i sin (
k)/
n + i sin (![]() +
2
+
2![]() k)/
n ) ] ,где
k
= 0,1,2, . . ., n – 1 .
k)/
n ) ] ,где
k
= 0,1,2, . . ., n – 1 .
Умножение
КЧ теперь сводится к умножению их модулей
и сложению аргументов, а деление КЧ к
делению модулей и вычитанию аргументов.
Появление n
решений при извлечении корня связано
с тем, что все значения Arg
z
= (![]() +
2 k
+
2 k
![]() )
уменьшаются
в n
раз и самые первые n
значений аргумента становятся меньше
3600
, т.е. становятся главными
значениями аргумента - arg
z
. Они различны,
но при возведении корней в степень n
получаем
одинаковый
результат.
)
уменьшаются
в n
раз и самые первые n
значений аргумента становятся меньше
3600
, т.е. становятся главными
значениями аргумента - arg
z
. Они различны,
но при возведении корней в степень n
получаем
одинаковый
результат.
Показательная форма КЧ.
Существует
формула Эйлера exp
(i
![]() )
= cos
)
= cos
![]() + i
sin
+ i
sin
![]() , которая
приводит к показательной
форме КЧ
, которая
приводит к показательной
форме КЧ
z
= a + i b = r (cos
![]() + i sin
+ i sin![]() )
= r exp (i
)
= r exp (i![]() )
)
( I ) ( II ) ( III )
В алгебраической форме ( I ) КЧ удобно складывать и вычитать, а в тригонометрической форме ( II ) и в показательной ( Ш ) умножать, делить.
r1
exp
(i
![]() 1)
r2
exp
(i
1)
r2
exp
(i
![]() 2)
= r1
r2
exp i (
2)
= r1
r2
exp i (![]() 1
+
1
+
![]() 2
2![]()
r1
exp
(i
![]() 1)
/ r2
exp
(i
1)
/ r2
exp
(i
![]() 2)
= r1/
r2
exp i (
2)
= r1/
r2
exp i (![]() 1
-
1
-
![]() 2
2![]()
(
r exp i
![]() )n
= rn
exp i n
)n
= rn
exp i n
![]()
(
r exp i
![]() )1/n
= r1/n
exp i (
)1/n
= r1/n
exp i (![]() +2
k
+2
k![]() )/
n , k = 0,1,2,3, . . . , n - 1 .
)/
n , k = 0,1,2,3, . . . , n - 1 .
Если
z
= a
> 0 , то z
= a(cos
0 + i
sin
0) ,![]() = 0 и формула
a1/n
= r1/n
exp
i
(2 k
= 0 и формула
a1/n
= r1/n
exp
i
(2 k
![]() )/
n
определяет
n
корней
действительного числа. Здесь модуль
r1/n
любой
из корней
числа.
)/
n
определяет
n
корней
действительного числа. Здесь модуль
r1/n
любой
из корней
числа.
Н апример,
апример,
![]() =
(cos
0 + i sin 0)1/4
= cos
2
=
(cos
0 + i sin 0)1/4
= cos
2![]() k/
4 + i sin 2
k/
4 + i sin 2![]() k/
4 ,
k/
4 ,
где k = 0,1,2, 3. Получаем корни z0 = 1, z1 = i , z2 = - 1 , z3 = -i .
Проверка ( 1 )4 = ( i )4 = ( -1 )4 = ( -i )4 = 1 .
Если
z
=
- a
< 0,
то
z = a(cos
![]() + i sin
+ i sin
![]() )
,
)
,
![]() =
=![]() и
и
(-a)1/n
= r1/n
exp i (![]() +2
k
+2
k![]() )/
n ,где
k
= 0,1,2, . ., n – 1
)/
n ,где
k
= 0,1,2, . ., n – 1
Пр.
Вычислить (
- 81 )1/.4
. Решение
(- 81 )1/
4 = ( -
1 81 )1/4
=
![]() (
cos
(
cos
![]() + i
sin
+ i
sin
![]() )1/
4
)1/
4
=
3 ( cos (![]() +
2 k
+
2 k![]() )/
4 + i sin (
)/
4 + i sin (![]() +
2 k
+
2 k![]() )/
4 ) , k = 0, 1, 2, 3 .
)/
4 ) , k = 0, 1, 2, 3 .
z 0
= 3(
cos
0
= 3(
cos
![]() /
4 + i sin
/
4 + i sin![]() /4
) = 3
/4
) = 3![]() /2(
1 + i )
/2(
1 + i )
z1
= 3 ( cos (![]() /4
+
/4
+![]() /2
) + i sin(
/2
) + i sin(![]() /4
+
/4
+![]() /2))
= 3
/2))
= 3![]() /2(
1 - i )
/2(
1 - i )
z2
= 3 ( cos (![]() /4
+
/4
+![]() ) + i sin(
) + i sin(![]() /4
+
/4
+![]() )
) = 3
)
) = 3![]() /2(
-1 - i )
/2(
-1 - i )
z3
= 3 ( cos
(![]() /4
+ 3
/4
+ 3![]() /2)
+ i
sin(
/2)
+ i
sin(![]() /4
+ 3
/4
+ 3![]() /2)
) = 3
/2)
) = 3![]() /2(
1 - i
)
/2(
1 - i
)
Решения
изображают 4 вектора с r
= 3![]() /2
и
/2
и
![]() 0=
0=
![]() /4,
/4,
![]() 1
=3
1
=3![]() /4,
/4,
![]() 2
=5
2
=5![]() /4
/4
![]() 3
=7
3
=7![]() /4
/4
Таблица 1 . 00 300 450 600 900
sin
0 1/2
![]() /2
/2![]() /2
1
/2
1
cos
1
![]() /2
/2![]() /2
½ 0
/2
½ 0
Таблица 2
![]() 900-
900-
![]() 900+
900+
![]() 1800-
1800-
![]() 1800+
1800+
![]() 2700
-
2700
-
![]() 2700
+
2700
+
![]() 3600
-
3600
-
![]() .
.
sin
sin![]() cos
cos![]() cos
cos![]() sin
sin![]() - sin
- sin![]() - cos
- cos![]() - cos
- cos![]() - sin
- sin![]()
cos
cos![]() sin
sin![]() - sin
- sin![]() - cos
- cos![]() - cos
- cos![]() - sin
- sin![]() sin
sin![]() cos
cos![]()
Пр. Даны z1 = 12 ( cos 2250 + i sin 2250) , z2 = 3/2 ( cos 750 + i sin 750). Найти z1 z2 , z1 /z2
z1 z2 = 18 ( cos (2250+ 750) + i sin (2250 + 750)) = 18 (cos(3600 – 600) + i sin(3600 – 600)) =
=
18 ( cos 600
- i sin 600
) = 18 ( ½ - i
![]() /2
) = 9 - 9 i
/2
) = 9 - 9 i![]()
z1/ z2 = 8 (cos (2250– 750) + i sin(2250 – 750)) = 18 (cos (1800 – 300) + i sin (1800– 300)) =
=
8 (- cos 300
+ i sin 300
) = 8 ( -
![]() /2
+ i ½ ) = - 4
/2
+ i ½ ) = - 4![]() + 4 i
+ 4 i
Ряды с КЧ.
Рассмотрим
ряд
![]() (a)
с общим членом zn
= xn
+ i
yn
. Он разделяется
на два ряда с действительными числами
(a)
с общим членом zn
= xn
+ i
yn
. Он разделяется
на два ряда с действительными числами
![]() и
и![]() . Из сходимости этих рядов следует
сходимость исходного ряда. Составим
ряд
. Из сходимости этих рядов следует
сходимость исходного ряда. Составим
ряд![]() (b)
из модулей |zn|
=
(b)
из модулей |zn|
=
![]() .
Т.к. |xn|
< rn
, |yn|
< rn
, то из
сходимости ряда (b)
по признаку сравнения следует
сходи-мость рядов
.
Т.к. |xn|
< rn
, |yn|
< rn
, то из
сходимости ряда (b)
по признаку сравнения следует
сходи-мость рядов
![]() и
и![]() ,
что обеспечиваетабсолютную
сходимость
ряда
(a).
Т.о., ряд с КЧ абсолютно сходится, если
сходится ряд из модулей этих КЧ.
,
что обеспечиваетабсолютную
сходимость
ряда
(a).
Т.о., ряд с КЧ абсолютно сходится, если
сходится ряд из модулей этих КЧ.
Рассмотрим
степенной ряд
![]() (с),
где an
, z
- КЧ. Составим
ряд из модулей
(с),
где an
, z
- КЧ. Составим
ряд из модулей
![]() ,
гдеAn
= |an|
, r
= |z|.
По теореме
Абеля такой ряд сходится в интервале
,
гдеAn
= |an|
, r
= |z|.
По теореме
Абеля такой ряд сходится в интервале
-R < r < R . Следовательно, степной ряд (с) сходится для z из круга радиуса R : |z| < R.
Области и линии на комплексной плоскости.
От КЧ z = a + ib перейдем к комплексной переменной величине (КП) z = x + iy , где x, y могут изменяться в определенных пределах. Если эти изменения зависят от одного параметра : x = x(t), y = y(t), t1 < t < t2 , то КП z = z(t) определяет непрерывную кривую на комплексной плоскости.
Пр.

От
системы параметрических уравнений
эллипса x
= a
cos
t
, y
= b
sin
t
, 0 < t
< 2![]()
переходим
к комплексному представлению кривой
z
= a
cos
t
+ ib
sin
t.
При a
= b
= r
получаем
представление окружности z
= r
eit
или |z|
= r
. Если центр
окружности смещен в точку z1
=
![]() ,
то z
= z1
+ r
eit
.
,
то z
= z1
+ r
eit
.
Опр.
![]() -окрестностью
точки а
наз.множество
всех точек z
, для
которых
-окрестностью
точки а
наз.множество
всех точек z
, для
которых
|z
– a|
<![]() ,
,![]() >0
.Областью
G
комплексной
плоскости наз. множество точек плоскости
каждая из которых имеет свою
>0
.Областью
G
комплексной
плоскости наз. множество точек плоскости
каждая из которых имеет свою
![]() -окрестность
и может быть соединена с другими точками
непрерывной кривой. Границей
области G
наз. множество
точек, которые не принадлежат G
, но в ближайшей
окрестности имеют точки из G.
-окрестность
и может быть соединена с другими точками
непрерывной кривой. Границей
области G
наз. множество
точек, которые не принадлежат G
, но в ближайшей
окрестности имеют точки из G.
Область комплексной плоскости, в пределах которой изменяется КП, наз. односвязной, если ее ограничивает непрерывная, замкнутая и не самопересекающаяся линия (кривая Жордана). Если область ограничена несколькими замкнутыми линиями, то она наз. многосвязной. В качестве дополнительного контура может быть отдельная точка или линия.

Круг
|z
– z| < R Кольцо
r
< |z – z0|
< R Сектор
![]() <
arg (z – z0)
<
<
arg (z – z0)
<
![]()

Определение функции комплексного переменного.
Опр. Если каждому значению переменной z = x + iy из множества D по правилу f сопоставляется одно или несколько значений w = u + i v из множества W , то f наз. комплексной функцией комплексного переменного (ФКП). D – область определения, W – область значений функции w = f(z).
Функция наз. однозначной, если каждому значению z ставится в соответствие одно значение w и многозначной в ином случае.
Е слиw
= u
+ i
v
есть функция
от z
= x
+ iy
, то u
и
v
являются
действительными функциями от х,
у, и наоборот,
всякое выражение w
=u(x,y)+i
v(x,y)
есть ФКП от
z
=x
+ iy.
ФКП w
= u(x,y)
+ i
v(x,y)
имеет
условную запись w
= f(z)
, которая не
означает, что функция зависит от х
и у
только в комбинации x
+ i
y.
Пр. Выражение
x
+ 2i
y
является
функцией переменной z
= x
+ i
y.
слиw
= u
+ i
v
есть функция
от z
= x
+ iy
, то u
и
v
являются
действительными функциями от х,
у, и наоборот,
всякое выражение w
=u(x,y)+i
v(x,y)
есть ФКП от
z
=x
+ iy.
ФКП w
= u(x,y)
+ i
v(x,y)
имеет
условную запись w
= f(z)
, которая не
означает, что функция зависит от х
и у
только в комбинации x
+ i
y.
Пр. Выражение
x
+ 2i
y
является
функцией переменной z
= x
+ i
y.
Пр. Дана функция w = z2 + z .
Найти её значение при z = 1 + i .
Решение. w = (1 + i)2 + (1 + i) = 1 + 3i .
f
(1
+ i)
![]() (1 + 3i)
(1 + 3i)
Функция
наз. ограниченной,
если ее модуль |w|
=![]() не
превосходит некоторого конечного числа.
Предел функции lim
f(z)
= a
при z
не
превосходит некоторого конечного числа.
Предел функции lim
f(z)
= a
при z
![]() z0
складывается
из пределов функций u(x,y),
v(x,y)
при (x,y)
z0
складывается
из пределов функций u(x,y),
v(x,y)
при (x,y)
![]() (x0,y0).
Функция
f(z)
непрерывна
в точке z
, если функции
u(x,y),
v(x,y)
непрерывны
в этой точке.
(x0,y0).
Функция
f(z)
непрерывна
в точке z
, если функции
u(x,y),
v(x,y)
непрерывны
в этой точке.
Принципиально новый момент – геометрический смысл ФКП. Т.к. функция f(z) сопоставляет каждой точке z одной плоскости точку w другой плоскости, то её геометрический смысл - отображать плоскость z в плоскость w .При этом линии и фигуры, описанные изменяющейся z , переходят в линии и фигуры совершенно другой конфигурации.
Имеем некоторую кривую F(x,y) = 0 и ФКП w = u(x,y) + i v(x,y). Надо найти отображение этой кривой на плоскость uOv. Переход к новой системе координат определяют уравнения u = u(x,y), v = v(x,y) . Совершим обратное преобразование
x = x(u,v), y = y(u,v) и перейдем в уравнении кривой к новым переменным
F(x(u,v), y(u,v)) = 0 . Это уравнение определяет отображение исходной кривой.
Пр.
В какую кривую отображается окружность
|z|
=
![]() с помощью
функции w
= z2?
с помощью
функции w
= z2?
Решение.
Имеем
окружность x2
+ y2
= 2 и w
= (x
+ i
y)2
= ( x2
– y2)
+ 2xy
i
. Получаем
систему уравнений перехода к новым
координатам u
= x2
– y2
, v
= 2xy.
Оба уравнения
возведем в квадрат и сложим u2
+ v2
= (x2
+ y2)2
![]() x2
+ y2
=
x2
+ y2
=
![]() .
Заменим переменные в уравнении окружности
и получим u2
+ v2
= 4 , т.е.
окружность |w|
= 2 , причем,
при прохождении исходной окружности
вторая проходится дважды.
.
Заменим переменные в уравнении окружности
и получим u2
+ v2
= 4 , т.е.
окружность |w|
= 2 , причем,
при прохождении исходной окружности
вторая проходится дважды.

|z|
=
![]()
![]()
![]() eit
, (0 < t < 2
eit
, (0 < t < 2![]() ),
),
w = z2 = 2 ei 2t
Элементарные функции комплексной переменной.
Основные элементарные функции для КП подлежат переопределению. Наиболее просто вводится степенная функция по формуле Муавра
zn
= (x + i y)n
= rn(
cos n![]() + i sin n
+ i sin n![]() )
)
т.е.
Re
zn
= rn
cos n![]() , Im zn
= rn
sin
n
, Im zn
= rn
sin
n![]() , r =
, r =![]() ,
arg zn
= n
,
arg zn
= n![]() .
.
Действительные функции ex, sin x, cos x, sh x, ch x представим в виде степенных рядов и заменим в них x на z .
ez
=
1 + z +
![]()
![]() (
1 )
(
1 )
sin
z = z -
![]() (
2 )
(
2 )
cos
z = 1 -
![]() ( 3 )
( 3 )
sh
z
=
![]() = z
+
= z
+
![]() (
4 )
(
4 )
ch
z
=
![]() = 1 +
= 1 +![]() (
5 )
(
5 )
Эти ряды абсолютно сходятся на всей комплексной плоскости, т.к. сходятся ряды из |z| . Cравнение рядов дает простые соотношения для функций. Заменим в ( 1 ), ( 2 ), ( 3 ) z на iz . Тогда из ( 1 ) получаем формулу Эйлера (1743 г.)
ei
z =
1 + i z -
![]() = cos z + i sin z(
6 )
= cos z + i sin z(
6 )
а в ( 2 ) и ( 3 ) все слагаемые примут положительный знак и получим
cos iz = ch z , sin iz = i sh z ( 7 )
Соотношения ( 7 ) после замены z на iz принимают вид
ch iz = cos z , sh iz = i sin z ( 8 )
Для КП справедливы формулы
![]() ,
,
![]()
sin(z1 + z2) = sin z1 cos z2 + cos z1 sin z2 ( 9 )
cos(z1 + z2) = cos z1 cos z2 - sin z1 sin z2
Для гиперболических функций имеются соотношения аналогичные ( 9 ) и основное тождество ch2z - sh2z = 1 ( 10 )
Определим свойства функций ( 1 ) - ( 5 ) .
Функция ez ez = ex + i y = ex ei y = ex ( cos y + i sin y ) ( 11 )
т.е.
Re
ez
= ex
cos y , Im ez
= ex
sin y , | ez
|
= ex
, y – аргумент,
его
главное
значение
arg
ez
= y + 2k![]() ,где
целое
число
k
определяется
условием
-
,где
целое
число
k
определяется
условием
-
![]() <
y + 2k
<
y + 2k![]() <
<![]() .
.
При
перемещении вдоль мнимой оси функция
ez
периодическая,
период 2![]() i
,
i
,
Функция sin z Используем формулы ( 9 ), ( 7 ), ( 10 )
sin z = sin(x + i y) = sin x cos iy + cos x sin iy = sin x ch y + i cos x sh y ( 12 )
т.е. Re sin z = sin x ch y , Im sin z = cos x sh y , arg sin z = arctg [ ctg x th y ],
|sin
z| = [sin2x
ch2y
+ cos2x
sh2y
]1/2
= [sin2x(1+
sh2y)
+ cos2x
sh2y
]1/2
=
![]()
При
перемещении вдоль действительной оси
функция sin
z
периодическая,
период 2![]() .
.

Функция cos z Используем формулы ( 9 ), ( 7 ), ( 10 )
cos z = cos(x + i y) = cos x cos iy - sin x sin iy = cos x ch y - i sin x sh y ( 13 )
т.е. Re cos z = cos x ch y , Im cos z = - sin x sh y , arg cos z = arctg [ - tg x th y ],
|cos
z| = [cos2x
ch2y
+ sin2x
sh2y
]1/2
=
![]()
При
перемещении вдоль действительной оси
функция cos
z
периодическая,
период 2![]() .
.
Функция sh z Используем формулы ( 9* ), ( 8 ), ( 10 )
sh z = sh(x + i y) = sh x ch iy + ch x sh iy = sh x cos y + i ch x sin y ( 14 )
т.е. Re sh z = sh x cos y , Im sh z = ch x sin y , arg sh z = arctg [ ctg x th y ],
|sh
z| = [sh2x
cos2y
+ ch2x
sin2y
]1/2
=
![]()
При
перемещении вдоль мнимой оси функция
sh
z
периодическая,
период 2![]() i
,
i
,
Функция ch z Используем формулы ( 9* ), ( 8 ), ( 10 )
ch z = ch(x + i y) = ch x ch iy + sh x sh iy = ch x cos y + i sh x sin y ( 15 )
т.е. Re ch z = ch x cos y , Im ch z = sh x sin y , arg ch z = arctg [ th x tg y ],
|ch
z| = [ch2x
cos2y
+ sh2x
sin2y
]1/2
=
![]()
При
перемещении вдоль мнимой оси функция
ch
z
периодическая,
период 2![]() i
,
i
,
Функции tg z, ctg z, sh z, ch z определяют формулы
![]()
Функция
ln
z
Натуральный логарифм числа z
= r(
cos
![]() + i
sin
+ i
sin
![]() ) есть КЧ
(x
+ i
y),
удовлетворяющее
равенству
) есть КЧ
(x
+ i
y),
удовлетворяющее
равенству
ex
+ i y
= r ( cos
![]() + i sin
+ i sin![]() )или
ex
(
cos y + i sin y ) = r ( cos
)или
ex
(
cos y + i sin y ) = r ( cos
![]() + i sin
+ i sin![]() )
)
Откуда
следует ex
= r
или x
= ln
r
, y
=
![]() + 2k
+ 2k![]() , т.е.
, т.е.
Ln
[ r ( cos
![]() + i sin
+ i sin![]() ) ] = ln r + i(
) ] = ln r + i(![]() + 2k
+ 2k![]() )(
16 )
)(
16 )
Логарифм КЧ равен логарифму его модуля плюс i , умноженное на одно из значений аргумента.
Общая показательная функция az является многозначной az = ez ln a ( 17 )
Функция
arcsin
z
Прямую функцию z
= sin
w
=
![]() умножим на
2i
ei
w
и получим квадратное уравнение e2i
w
- 2i
ei
w
- 1 = 0 . Его
решение ei
w
= iz
+
умножим на
2i
ei
w
и получим квадратное уравнение e2i
w
- 2i
ei
w
- 1 = 0 . Его
решение ei
w
= iz
+
![]() прологарифмируем
и получим
прологарифмируем
и получим
w
= arcsin
z
= -i
ln(iz
+
![]() )
(
18 )
)
(
18 )
Аналогично
вычисляются: arccos
z
= -i
ln(z
+
![]() )
, arctg
z
=
)
, arctg
z
=
![]() ( 19 )
( 19 )
Производная ФКП.
Производная однозначной ФКП w = f(z) определяется как предел отношения приращения функции к приращению аргумента
lim
![]() =
=
![]() при
при
![]() ( 20 )
( 20 )
Если
предел существует и не зависит от способа
стремления
![]() к нулю, то функция
к нулю, то функция
w = f(z) наз. аналитической в окрестности точки z .
Определим
условие независимости предела ( 20 ) от
способа стремления
![]() к нулю. Процесс
к нулю. Процесс![]() определяют два процесса
определяют два процесса![]() и
и![]() .
Их относительная скорость
.
Их относительная скорость h
может быть различной. Представим
отношение
h
может быть различной. Представим
отношение
![]() =
=![]() как функцию отh
и определим
условие обращения этой функции в
константу.
как функцию отh
и определим
условие обращения этой функции в
константу.
Заменим
![]() в отношении
в отношении![]() на дифференциалы и затем перейдем к
пределу
на дифференциалы и затем перейдем к
пределу

![]() du
= u`x
dx
+ u`y
dy
,
du
= u`x
dx
+ u`y
dy
,
![]() dv
= v`xdx
+ v`ydy
dv
= v`xdx
+ v`ydy
![]()
![]()

![]() =
=
 =
=
![]()
Независимость производной от h выполняется при B = i A или u`y + iv`y = i(u`x + iv`x)
Отсюда следуют необходимые условия дифференцируемости Коши – Римана
![]() ,
,
![]() ( 21
)
( 21
)
Если частные производные от u и v непрерывны в области D и выполняется условие Коши – Римана, то функция w = f(z) дифференцируема в этой области.
Поскольку частные производные связаны между собой, то выражение для полной производной имеет разные формы
![]() =
А =
=
А =
![]() =
=![]() =
=![]() =
=![]() ( 22
)
( 22
)
Пр.
Проверим аналитичность функции w
= z*
по формулам
( 20 ) и ( 21 ). Пусть движение от точки z
+![]() z
к точке
z
идет по
кривой y
= g(x).
Тогда при
z
к точке
z
идет по
кривой y
= g(x).
Тогда при
![]()
lim
![]() =
lim
=
lim
![]() = lim
= lim
![]() =
=![]()
т.е. предел отношения приращений функции и аргумента включает тангенс угла наклона касательной к кривой y = g(x) , которая произвольна. Имеем u = x , v = -y . Тогда u’x = 1, v’y = - 1 , т.е. условия Коши – Римана ( 20 ) для w = z* не выполняются.
ФКП w = u(x,y) + i v(x,y) , зависящая от двух переменных , всегда является аналитической, если фактически зависит только от их комбинации x + i y , т.е. является функцией одной независимой переменной z . Покажем, что это требование эквивалентно условию Коши – Римана.
Заменим в w(x,y) x на z – iy и продифференцируем по у .
![]() =
=
![]() +i
[
+i
[![]() ]
=
]
=
=
-i![]() +i
[
+i
[![]() ]
=
]
=![]()
![]()
При
выполнении условий Коши – Римана
получаем
![]() , т.е. функцияw
не зависит
от у , а
только от z
. Т.о., замена
в функции действительной переменной
f(x)
аргумента
х на
КП z
приводит к
аналитической функции f(z)
.
, т.е. функцияw
не зависит
от у , а
только от z
. Т.о., замена
в функции действительной переменной
f(x)
аргумента
х на
КП z
приводит к
аналитической функции f(z)
.
Пр. Функция w = x + 2i y = z + iy не аналитическая, а функция w = x2 – y2 + 2ixy = z2 - аналитическая.
Вычислим производные от нескольких элементарных функций.
1.
w = z2
. Т.к.u
= x2
– y2,
v = 2xy, то![]() =
=![]() =
=
![]() =
2x
+ i2y = 2z
=
2x
+ i2y = 2z
Аналогично
доказывается общая формула
![]() = n
zn
- 1
( 23 )
= n
zn
- 1
( 23 )
2.
w
=
ez
. Т.к.
по
( 11 ) ez
= ex
(cos
y + i sin y) , то
![]() =
=
![]() = ex
cos
y + i sin y = ez
= ex
cos
y + i sin y = ez
Производная
от экспоненты равна самой функции
![]() =ez
(
24 )
=ez
(
24 )
3. w = sin z . Т.к. по ( 12 ) sin z = sin x ch y + i cos x sh y , то c учетом ( 13 ) имеем
![]() =
=![]() = cos
x ch y - i sin x sh y = cos z (
25 )
= cos
x ch y - i sin x sh y = cos z (
25 )
4.
w
= ln z . Т.к.
по
( 16 )
ln z = ln (![]() )
+ i [ arctg(
)
+ i [ arctg(![]() )
+ 2k
)
+ 2k![]() ],
то
],
то
![]() =
=
![]() =
=![]() + i
+ i
![]() =
=
![]() =
=
![]() ( 26
)
( 26
)
Аналогично вычисляются следующие производные
( cos z )` = - sin z , ( sh z )` = ch z , ( ch z )` = sh z ,
(
arcsin z )` =
![]() , (arcos z )` =
, (arcos z )` =![]() , ( arctg z )` =
, ( arctg z )` =![]() (
27 )
(
27 )
Таким образом, производные от основных элементарных функций от действительных и комплексных переменных полностью совпадают, также как и все правила дифференцирования.
Продифференцируем первое уравнение из ( 21 ) по х , второе по у и сложим их
![]() ,
,
![]() ( 28
)
( 28
)
В результате получаем уравнение Лапласа для u и аналогичным образом для v , т.е. мнимая и действительная части всякой аналитической функции являются функциями гармоническими. Их общее свойство: изменение функции вдоль х и вдоль у идет с одинаковым по модулю ускорением. Но не всякое сочетание двух гармонических функций образует аналитическую функцию. Функции u и v должны быть сопряженными. Зная u можно построить v и наоборот.
Пр. Дана действительная часть u(x,y) = x2 – y2 – x дифференцируемой функции f(z), где z = x + iy. Найти функцию f(z).
Решение.
Вычисляем
![]() . Т.к.
. Т.к.![]() ( 1 условие Коши – Римана), то
( 1 условие Коши – Римана), то![]() .
Это ДУ интегрируем
.
Это ДУ интегрируем![]()
![]() v(x,y)
= 2xy
– y
+
v(x,y)
= 2xy
– y
+
![]() ,
где
,
где
![]() -
произвольная функция. Это решение
дифференцируем пох
:
-
произвольная функция. Это решение
дифференцируем пох
:
![]() =2y
+
=2y
+
![]() .
Т.к.
.
Т.к.![]() ( 2 условие Коши – Римана), то
( 2 условие Коши – Римана), то![]() = -2y
-
= -2y
-
![]() .
Но из условия задачи следует
.
Но из условия задачи следует![]() . Сравнение производных дает
. Сравнение производных дает![]() = 0 или
= 0 или![]() =const
, т.е сопряженная функция равна v(x,y)
= 2xy
– y
+ С .
=const
, т.е сопряженная функция равна v(x,y)
= 2xy
– y
+ С .
Ответ: f(z) = (x2 – y2 – x) + i (2xy – y +С) = (x2 – y2) +i 2xy + (x + i y) + C = z2 + z + C
Конформное отображение.
Дана
аналитическая функция w
= f(z)
, которая
сопоставляет точкам области D
точки области W.
Выберем в
D
две близко расположенные точки m
и
m1
.
Им соответствуют
точки М и
М1 в
W.
Отрезки mm1
и MM1
соединяют z
с z
+![]() z
и w
с w
+
z
и w
с w
+
![]() w
. Этим
векторам соответствуют КЧ
w
. Этим
векторам соответствуют КЧ
![]() z
и
z
и
![]() w
.
w
.

Отношение
модулей векторов равно
![]() .
Перейдем к пределуm1
.
Перейдем к пределуm1
![]() m
m
lim
![]() = lim
= lim
![]() =|f
`(z)|
(
=|f
`(z)|
(![]() z
z
![]() 0)
0)
т.е. модуль производной показывает во сколько раз длина отрезка в окрестности точки z больше длины отображения этого отрезка.
Пусть
m1
приближается
к m
вдоль линии
l
. Тогда соответствующее движение М1
к М пойдет
по линии L
. Аргумент
КЧ
![]() z
определяет
угол между вектором mm1
и осью Ох
, а аргумент
z
определяет
угол между вектором mm1
и осью Ох
, а аргумент
![]() w
между
вектором ММ1
и осью Ou.
Разность
этих аргументов определит угол между
векторами mm1
и ММ1
, причем,
разность аргументов равна аргументу
частного
w
между
вектором ММ1
и осью Ou.
Разность
этих аргументов определит угол между
векторами mm1
и ММ1
, причем,
разность аргументов равна аргументу
частного
arg
![]() w
- arg
w
- arg![]() z
= arg
z
= arg![]() , (
, (![]() )
)
При
m1
![]() m
секущие
mm1
и ММ1
становятся
касательными и предел
m
секущие
mm1
и ММ1
становятся
касательными и предел
lim
arg![]() = arg f `(z) (
= arg f `(z) (![]() z
z
![]() 0)
0)
о пределит
угол между касательной кl
в точке z
и касательной
к L
в точке w,
т.е.
arg
f
`(z)
дает угол
поворота прямой в точке z
в результате
преобразования f(z).
Этот угол
не зависит от параметров линии. Поэтому,
при прохождении через точку z
двух линий l
и
l1
под углом
пределит
угол между касательной кl
в точке z
и касательной
к L
в точке w,
т.е.
arg
f
`(z)
дает угол
поворота прямой в точке z
в результате
преобразования f(z).
Этот угол
не зависит от параметров линии. Поэтому,
при прохождении через точку z
двух линий l
и
l1
под углом
![]() их отображения
L
и
L1
будут
пересекаться под тем же углом
их отображения
L
и
L1
будут
пересекаться под тем же углом
![]() .
.
Сохранение угла приводит к тому, что бесконечно малый треугольник в окрестности точки z отображается в подобный треугольник в плоскости w, т.е. его стороны изменяют длины в отношении |f `(z)| :1 и поворачиваются на угол arg f `(z) . Это свойство подобия следует из факта существования производной, т.е. аналитичности функции f(z).
Опр. Конформным ( подобным ) отображением наз. отображение с помощью аналитической функции.
Пр. При помощи функции w = z3 отобразить на плоскость uOv линию y = x .
Решение. Имеем w = ( x + iy)3 = x3 + 3x2iy + 3x(iy)2 + (iy)3 = (x3 -3xy2) + (3x2y – y3) i , т.е.

u = x3 - 3xy2 , v = 3x2y – y3 . Определим значение этих координат для точек линии y = x : u = - 2x3 , v = 2x3, т.е. v = - u . Это биссектриса 2 и 4 квадранта.
Пр. При помощи функции w = 2z +1 отобразить на плоскость uOv окружность x2+y2=1.
Решение.
Имеем w
= 2(x
+ iy)
+ 1 = (2x
+ 1) + 2yi
, т.е. u
= (2x
+ 1) , v
= 2y
. Находим
обратное преобразование координат x
= (u
– 1)/2 , y
= v/2
и делаем
замену переменных в уравнении окружности
[(u
– 1)/2]2
+ [v/2]2
= 1
![]() (u
– 1)2
+ v2
= 4 . Отображение
есть окружность с радиусом 2 и центром
в точке (1;0).
(u
– 1)2
+ v2
= 4 . Отображение
есть окружность с радиусом 2 и центром
в точке (1;0).
Римановы поверхности
Функция наз. однозначной, если каждому значению z ставится в соответствие одно значение w и многозначной в ином случае.
Функция
z
= w2
однозначная,
а обратная функция w
=
![]() - многозначная, т.к. корнями являются
два комплексных сопряженных числа.
Однако, многозначную функцию можно
представить как однозначную, если
определять ее наримановой
поверхности.
Она состоит из нескольких плоскостей,
соединенных между собой вдоль некоторых
линий – разрезов.
- многозначная, т.к. корнями являются
два комплексных сопряженных числа.
Однако, многозначную функцию можно
представить как однозначную, если
определять ее наримановой
поверхности.
Она состоит из нескольких плоскостей,
соединенных между собой вдоль некоторых
линий – разрезов.
Пусть
w
= r
ei
t
определена
в верхней полуплоскости. Тогда arg
w
= t![]() (0,
(0,![]() )
,но arg
w2
= arg
(r2
e2i
t
)
)
,но arg
w2
= arg
(r2
e2i
t
)
![]() (0,
2
(0,
2![]() ) , т.е. функция
z
= w2
отобразит
верхнюю полуплоскость на всю плоскость.
Исключение составят точки оси Ох
при x
> 0 ( t
= 0 ). Эта линия
наз. разрезом.
Такую
плоскость с разрезом обозначим T1.
Можно
говорить об обратном переходе – w
однозначная
функция от z
в области T1
: w
=
) , т.е. функция
z
= w2
отобразит
верхнюю полуплоскость на всю плоскость.
Исключение составят точки оси Ох
при x
> 0 ( t
= 0 ). Эта линия
наз. разрезом.
Такую
плоскость с разрезом обозначим T1.
Можно
говорить об обратном переходе – w
однозначная
функция от z
в области T1
: w
=
![]() ,
при условииIm
,
при условииIm![]() >
0 .
>
0 .
На
берегах разреза при t
![]() 0 и t
0 и t
![]() имеем
z
имеем
z
![]() |z|
> 0 и w
=
|z|
> 0 и w
=
![]() .На верхнем
берегу выберем w
=
.На верхнем
берегу выберем w
=
![]() ,на нижнем
w
= -
,на нижнем
w
= -![]() .
.
Пусть
w
= r
ei
t
определена
в нижней полуплоскости. Тогда функция
z
= w2
отобразит
её на плоскость Т2
, но знаки
на берегах разреза у функции w
=
![]() поменяются. Таким образом, на линии
разреза функцииw
=
поменяются. Таким образом, на линии
разреза функцииw
=
![]() однозначна, но для определения других
значений приходится использовать две
плоскостиТ1
, Т2
, что
обеспечивает полную однозначность
функции w
=
однозначна, но для определения других
значений приходится использовать две
плоскостиТ1
, Т2
, что
обеспечивает полную однозначность
функции w
=
![]() .
Плоскости
Т1
, Т2
связываются
в одну двулистную
область, где
верхний берег разреза в Т1
соединяется
с нижним берегом
разреза
Т2
и наоборот.
Точка z
= 0 наз. точкой
разветвления первого порядка. Если
выйти из точки z0
и вернуться
в неё по замкнутому контуру вокруг z
= 0 , то окажемся
на соседнем листе и функция
.
Плоскости
Т1
, Т2
связываются
в одну двулистную
область, где
верхний берег разреза в Т1
соединяется
с нижним берегом
разреза
Т2
и наоборот.
Точка z
= 0 наз. точкой
разветвления первого порядка. Если
выйти из точки z0
и вернуться
в неё по замкнутому контуру вокруг z
= 0 , то окажемся
на соседнем листе и функция
![]() поменяет свой знак.
поменяет свой знак.
В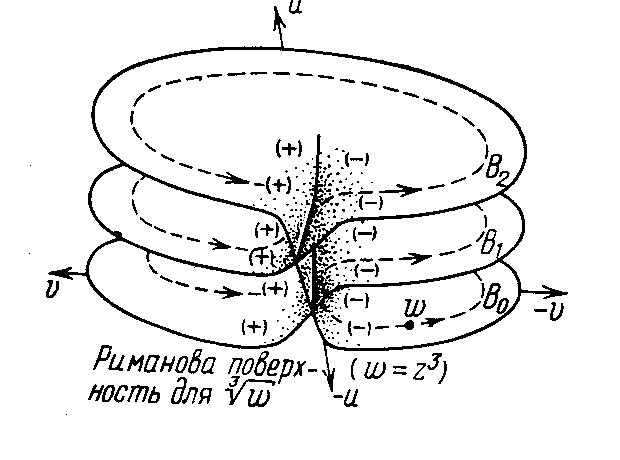 общем случае, если функцияz
= g(w)
однозначна
во всей плоскости w
, то это преобразование может перевести
w
в многолистную плоскость z
и обратная
функция w
= f(z)
будет
аналитическая на этой плоскости за
исключением точек, где g’(w)
= 0 . Это точки
разветвления обратной функции.
общем случае, если функцияz
= g(w)
однозначна
во всей плоскости w
, то это преобразование может перевести
w
в многолистную плоскость z
и обратная
функция w
= f(z)
будет
аналитическая на этой плоскости за
исключением точек, где g’(w)
= 0 . Это точки
разветвления обратной функции.
Криволинейный интеграл от ФКП.
По
аналогии с определенным интегралом![]() f(x)
dx
методом
интегральной суммы введем интеграл для
аналитической ФКП f(z).
Интегрировать
будем не вдоль оси Ох , а вдоль произвольной
кривой L
, соединяющей
точки z0
и z
комплексной
плоскости.
f(x)
dx
методом
интегральной суммы введем интеграл для
аналитической ФКП f(z).
Интегрировать
будем не вдоль оси Ох , а вдоль произвольной
кривой L
, соединяющей
точки z0
и z
комплексной
плоскости.

Разделим L на n участков точками z1, z2, . . . , zn = z .
На каждом отрезке zi – 1 zi длины
 zi
= zi
– zi
– 1 выделим
точку pi
и составим
произведение f(pi)
zi
= zi
– zi
– 1 выделим
точку pi
и составим
произведение f(pi)
 zi
.
zi
.Построим интегральную сумму
 f(pi)
f(pi)
 zi
.
zi
.Переход к пределу
 при условии |
при условии | z|
z| 0
даст КЧ.
0
даст КЧ.
lim
![]() f(pi)
f(pi)
![]() zi
=
zi
=
![]() f(z)
dz = J(
29 )
f(z)
dz = J(
29 )
Опр. Криволинейным интегралом от ФКП f(z) вдоль кривой L наз. предел интегральной суммы, полученный путем разбиения L на малые участки.
В общем случае КЧ J зависит от f(z), формы кривой L и существует для непрерывных и ограниченных функций и гладких кривых L . Кривая наз. гладкой, если она имеет непрерывно изменяющуюся касательную.
Выделим в J Re и Im части. Т.к. f(z) = u(x,y) + i v(x,y) , dz = dx + i dy , то
J
=
![]() u
dx – v dy + i
u
dx – v dy + i![]() v
dx + u dy(
30 )
v
dx + u dy(
30 )
т.е. J распадается на криволинейные интегралы от действительных переменных и сохраняет их общие свойства
10
![]() f(z)
dz
= -
f(z)
dz
= -
![]() f(z)
dz
, 20
f(z)
dz
, 20
![]() f(z)
dz
=
f(z)
dz
=
![]() f(z)
dz
+
f(z)
dz
+
![]() f(z)
dz
( 31 )
f(z)
dz
( 31 )
где K – промежуточная точка дуги АВ , и другие свойства.
Криволинейные интегралы вычисляют путем перехода к определенным интегралам. Если L задана в явной форме y = y(x) , a < x < b , то
![]() P(x,y)
dx
+ Q(x,y)
dy
=
P(x,y)
dx
+ Q(x,y)
dy
=
![]() {
P(x,y(x))
+ y`(x)
Q(x,y(x))}
dx
( 32 )
{
P(x,y(x))
+ y`(x)
Q(x,y(x))}
dx
( 32 )
Если
подынтегральная функция есть полный
дифференциал P
dx
+ Q
dy
= dU(x,y)
, при
выполнении условия
![]() ,
то
,
то
![]() dU(x,y)
= U(b,
y(b))
- U(a,
y(a))
, т.е.
значение
интеграла не зависит от формы кривой.
dU(x,y)
= U(b,
y(b))
- U(a,
y(a))
, т.е.
значение
интеграла не зависит от формы кривой.
При
параметрическом задании L
: z
= z(t)
,
![]() имеем
имеем
![]() f(z)
dz
=
f(z)
dz
=
![]() f(z(t))
z`(t)
dt
=
f(z(t))
z`(t)
dt
=
![]() Re
[f(z(t))
z`(t)]dt
+ i
Re
[f(z(t))
z`(t)]dt
+ i![]() Im
[f(z(t))
z`(t)]
dt
( 33 )
Im
[f(z(t))
z`(t)]
dt
( 33 )
Пр.1.
Вычислить интеграл
![]() f(z)
dz
, где f(z)
= (y
+1) – xi,
прямая АВ
соединяет
f(z)
dz
, где f(z)
= (y
+1) – xi,
прямая АВ
соединяет
т очкиzA
= 1 , zB
= -i
. Решение.
Имеем u
= y
+ 1 , v
= - x
. Уравнение
прямой y
= x
– 1 и dy
= 1. По формулам
(2.2 ) и ( 2.4 ) имеем
очкиzA
= 1 , zB
= -i
. Решение.
Имеем u
= y
+ 1 , v
= - x
. Уравнение
прямой y
= x
– 1 и dy
= 1. По формулам
(2.2 ) и ( 2.4 ) имеем
![]() f(z)
dz
=
f(z)
dz
=
![]() (y+1)
dx
– (-x)
dy
+ i
(y+1)
dx
– (-x)
dy
+ i
![]() (-x)
dx
+ (y+1)
dy
=
(-x)
dx
+ (y+1)
dy
=
=
![]()
![]() [
(x
– 1 + 1) – (-x)
] dx
+ i
[
(x
– 1 + 1) – (-x)
] dx
+ i
![]() [ (-x)
+ (x
– 1 + 1) ] dx
= - 1
[ (-x)
+ (x
– 1 + 1) ] dx
= - 1
Теорема Коши.
Если
f(z)
аналитическая
функция в односвязной области D
, то интеграл
![]() f(z)
dz
зависит
только от положения конечных точек А
и В кривой L
и не зависит
от формы кривой, или интеграл по замкнутой
кривой всегда равен нулю.
f(z)
dz
зависит
только от положения конечных точек А
и В кривой L
и не зависит
от формы кривой, или интеграл по замкнутой
кривой всегда равен нулю.
![]() f(z)
dz
= 0 (
34
)
f(z)
dz
= 0 (
34
)
Доказательство.
От
криволинейного интеграла по замкнутому
контуру на плоскости всегда можно
перейти к двойному интегралу по области,
ограниченной этим контуром по формуле
Грина
![]() P(x,y)
dx
+ Q(x,y)
dy
=
P(x,y)
dx
+ Q(x,y)
dy
=
![]()
В нашем случае
![]() u
dx
– v
dy
= -
u
dx
– v
dy
= -
![]() ;
;
![]() v
dx
+ u
dy
=
v
dx
+ u
dy
=
![]()
но
частные производные от аналитической
функции f(z)
удовлетворяют
условиям Коши – Римана
![]() ,
,![]() , которые обращают эти интегралы в ноль.
, которые обращают эти интегралы в ноль.
Неопределенный интеграл от ФКП.
Рассмотрим
выражение F(z)
=
![]() f(
f(![]() )d
)d![]() ,где f(
,где f(![]() )
–аналитическая
функция в области D
, а точки
z0
и
z
соединяет
произвольная гладкая кривая L
. Функция
F(z)
, удовлетворяет
равенству
)
–аналитическая
функция в области D
, а точки
z0
и
z
соединяет
произвольная гладкая кривая L
. Функция
F(z)
, удовлетворяет
равенству
F`(z) = f(z) ( 35 )
Действительно,
при h
![]() 0
0
F`(z)
= lim
![]() = lim
= lim![]() = lim
= lim![]() =
=
=
f(z)
+ lim![]() = f(z)
= f(z)
В
ближайшей окрестности точки z
функция
отличается от f(z)
на бесконечно
малую
![]() (h)
более высокого
порядка, чем h
. Т.к. F(z)
имеет производную, то она является
аналитической и наз. первообразной
для f(z).
Её значение
зависит от выбора точки z0
и она
определяется с точностью до константы.
(h)
более высокого
порядка, чем h
. Т.к. F(z)
имеет производную, то она является
аналитической и наз. первообразной
для f(z).
Её значение
зависит от выбора точки z0
и она
определяется с точностью до константы.
Опр. Совокупность всех первообразных ФКП f(z) наз. неопределенным интегралом
![]() f(z)
dz
= F(z)
+ C
(
36 )
f(z)
dz
= F(z)
+ C
(
36 )
Правила вычисления интегралов комплексных и действительных переменных совпадают.

Основная теорема интегрального исчисления.
Интеграл от функции f(z) , аналитической в D, равен приращению её первообразной функции, при переходе из начальной в конечную точку пути интегрирования
![]() f(z)
dz
= F(b)
- F(a)
(
37
)
f(z)
dz
= F(b)
- F(a)
(
37
)
Действительно,
интеграл
![]() f(
f(![]() )d
)d![]() =F(z)
+ C
дает
первообразную с точностью до константы.
Пусть z
=F(z)
+ C
дает
первообразную с точностью до константы.
Пусть z![]() z0
и контур
замыкается. Тогда по теореме Коши F(z0)
+ C
= 0 или C
= - F(z0)
, т.е. константа
равна первообразной в начальной точке.
z0
и контур
замыкается. Тогда по теореме Коши F(z0)
+ C
= 0 или C
= - F(z0)
, т.е. константа
равна первообразной в начальной точке.
Вычислим
теперь Пр.1 по формуле ( 37 ).
![]() f(z)
dz =
f(z)
dz =
![]() (1
– iz)dz =
(1
– iz)dz =
=![]()
![]() (1
– iz)d(1 – iz) =
(1
– iz)d(1 – iz) =
![]() (1
– iz)2
|1-i
=
(1
– iz)2
|1-i
=
![]() [
(1 + i2)2
– (1 – i)2
] = -1
[
(1 + i2)2
– (1 – i)2
] = -1
Пр.2
Вычислить
![]() z2
dz ,
если
прямая
АВ
соединяет
точки
zА
= 1, zB
= i
z2
dz ,
если
прямая
АВ
соединяет
точки
zА
= 1, zB
= i
![]() z2
dz =
z2
dz =
![]() z2dz
= 1/3 z3
|1i
= -1/3 (1 + i )
z2dz
= 1/3 z3
|1i
= -1/3 (1 + i )
Формула Коши.
Формула Коши выражает значение аналитической функции в любой точке z внутри области определения через её значения на произвольном контуре, окаймляющем точку.
f(z0)
=
![]() (
38
)
(
38
)

Доказательство.
Вокруг
выделенной точки z0
проведем
окружность
![]() радиуса
радиуса![]() и соединим её прямойАВ
с замкнутым контуром L.
Контур L’+
= AB
+
и соединим её прямойАВ
с замкнутым контуром L.
Контур L’+
= AB
+![]() -
+ BA
+ L+
,
охватывает кольцевую область, где
функция f(z)/(z0
– z)
аналитическая.
По теореме Коши ( 34
) и свойствам ( 31 )
-
+ BA
+ L+
,
охватывает кольцевую область, где
функция f(z)/(z0
– z)
аналитическая.
По теореме Коши ( 34
) и свойствам ( 31 )
имеем
![]() =
=
![]() -
-![]() -
-![]() +
+![]() =
0 ,т.е.
интеграл по внешнему контуру кольцевой
области равен интегралу по внутреннему
контуру того же направления
=
0 ,т.е.
интеграл по внешнему контуру кольцевой
области равен интегралу по внутреннему
контуру того же направления
![]() =
=
![]() (
39 )
(
39 )
Вычислим
его.
![]() =
=![]() +
+![]() = J1
+ J2
= J1
+ J2
J1
= f(z0)
![]() =
= =
i f(z0)
=
i f(z0)![]() = 2
= 2![]() i
f(z0)
i
f(z0)
В
J2
приращение
функции заменим на модуль его максимального
значения |f(z)–
f(z0)|
<![]() ,тогда J2
< |
,тогда J2
< |![]() |
= 2
|
= 2![]() .Т.к.
радиус
.Т.к.
радиус![]() произволен,
то при
произволен,
то при![]()
![]() 0
и
0
и![]() 0,
т.е. J2
= 0.
Отсюда
следует формула ( 38 ), которая дает явный
вид зависимости функции от z0
. Продифференцируем
( 38 ) по z0
n
раз и получим
0,
т.е. J2
= 0.
Отсюда
следует формула ( 38 ), которая дает явный
вид зависимости функции от z0
. Продифференцируем
( 38 ) по z0
n
раз и получим
f(n)(z0)
=
![]() (
40
)
(
40
)
Бесконечные ряды
Бесконечный
ряд из комплексных величин u1(z)
+ u2(z)
+. . .+ un(z)
+ . . =
![]() наз. абсолютно
сходящимся,
если сходится ряд из модулей этих величин
наз. абсолютно
сходящимся,
если сходится ряд из модулей этих величин
![]() .
Суммой ряда
наз. предел последовательности частичных
сумм Sn
: S
= lim
Sn
.Областью
сходимости степенного ряда
.
Суммой ряда
наз. предел последовательности частичных
сумм Sn
: S
= lim
Sn
.Областью
сходимости степенного ряда
![]()
![]() является круг радиусаR
с центром
в точке z0
: |z
– z0|
< R
(Теорема
Абеля). Радиус
сходимости R
= 1/
lim
является круг радиусаR
с центром
в точке z0
: |z
– z0|
< R
(Теорема
Абеля). Радиус
сходимости R
= 1/
lim
![]() при n
при n![]()
![]() .
Для степенного
ряда
.
Для степенного
ряда![]()
![]() с отрицательными степенями область
сходимости это вся плоскость за
исключением круга радиусаr
с центром
в z0
:
|z
– z0|
> r
. Действительно,
замена переменных z’
= (z
– z0)-1
даст
переход к ряду с положительными степенями
и радиусом сходимости r
. Тогда из
условия |z’|
< r
с отрицательными степенями область
сходимости это вся плоскость за
исключением круга радиусаr
с центром
в z0
:
|z
– z0|
> r
. Действительно,
замена переменных z’
= (z
– z0)-1
даст
переход к ряду с положительными степенями
и радиусом сходимости r
. Тогда из
условия |z’|
< r
![]() |z
– z0|
< 1/r
или
|z
– z0|
< 1/r
или
|z – z0| > r. Если r < R , то общей областью сходимости рядов двух типов будет кольцо r < |z – z0| < R . Ряды с отрицательными степенями определяют свойства функции вблизи точки разрыва.
Внутри области сходимости D сумма степенного ряда f(z) аналитическая функция. Поэтому возможен и обратный переход от f(z) к бесконечному ряду. Совершим его.
Выделим точку z0 в пределах области определения аналитической функции f(z) и представим f(z0) через значения этой функции на некотором контуре по формуле Коши
f(z0)
=
![]() (
38
)
(
38
)
Множитель 1/ (z – z0) разложим в ряд по формуле геометрической прогрессии
1/
(1 – q)
=
![]() qn
, |q|
< 1
qn
, |q|
< 1
и проверим ряд на абсолютную сходимость. Возможны два варианта.
(а)
![]() =
= =
=![]() ;
;
![]()
(b)
![]() =
= =
=![]() ;
;
![]()
Здесь а – фиксированная точка, а z0 - произвольная точка области D. Ряд (а) абсолютно сходится при |z0 –a| < |z – a| , a ряд (b) при |z0 –a| > |z – a|.
Р ассмотрим
случай области сходимости в виде круга
радиусаR
с центром
в точке а. В
качестве контура интегрирования по
переменной z
в ( 38 ) возьмем окружность L1
радиуса R1
< R
с центром
в точке а
и точкой z0
в ее пределах.
Тогда |z0
–a|
<|z
– a|
и ряд (а)
окажется равномерно сходящимся
относительно z0
.
ассмотрим
случай области сходимости в виде круга
радиусаR
с центром
в точке а. В
качестве контура интегрирования по
переменной z
в ( 38 ) возьмем окружность L1
радиуса R1
< R
с центром
в точке а
и точкой z0
в ее пределах.
Тогда |z0
–a|
<|z
– a|
и ряд (а)
окажется равномерно сходящимся
относительно z0
.
Заменим в ( 38 ) множитель 1/ (z – z0) на разложение ряда (а) и почленно проинтегрируем с учетом ( 40 )
f(z0)
=
![]() =
=
![]() (z0
– a)n
(z0
– a)n![]() =
=
![]()
![]() (z0
– a)n
(z0
– a)n
т.е. значение f(z) в любой точке круга |z – a| < R , где f(z) аналитическая функция, представляется рядом Тейлора
f(z)
= f(a) +
![]() (z – a) +
(z – a) +![]() (z
– a)2
+
(z
– a)2
+
![]() (z – a)3
+ . . . (
41
)
(z – a)3
+ . . . (
41
)
В случае, если аналитичность функции нарушается даже в отдельно взятой точке области сходимости, то область сходимости приобретает кольцевой характер.
Р ассмотрим
случай кольцевой области сходимостиr
< |z0
-a|
< R
с центром в
точке а .
Введем две
новые окружности L1(r
) и
L2(R)
вблизи
границ кольца с точкой z0
между ними.
Тогда формула Коши ( 38 ) включит два
интеграла по переменной z
ассмотрим
случай кольцевой области сходимостиr
< |z0
-a|
< R
с центром в
точке а .
Введем две
новые окружности L1(r
) и
L2(R)
вблизи
границ кольца с точкой z0
между ними.
Тогда формула Коши ( 38 ) включит два
интеграла по переменной z
f(z0)
=
![]() +
+
![]() (
42
)
(
42
)
где интегрирование идет в противоположных направлениях.
Для интеграла по L1 выполняется условие |z0 –a| > |z – a|, а для интеграла по L2 обратное условие |z0 –a| < |z – a|. Поэтому множитель 1/(z – z0) разложим в ряд (а) в интеграле по L2 и в ряд (b) в интеграле по L1 . В результате получаем разложение f(z) в кольцевой области в ряд Лорана по положительным и отрицательным степеням (z – a).
f(z)
=
![]() An
(z – a)n
(
43 )
An
(z – a)n
(
43 )
где
An
=
![]() =
=![]() ; A-n
=
; A-n
=
![]()
Разложение
по положительным степеням (z
– a)
наз. правильной
частью ряда
Лорана (ряд Тейлора), а разложение по
отрицательным степеням наз. главной
частью ряда
Лорана. При наличии n
членов в
главной части точка а
наз. изолированной
особой точкой или
полюсом n
– ого
порядка
функции f(z).
Если n
![]() ,
то точка а
наз. существенно
особой точкой.
,
то точка а
наз. существенно
особой точкой.
Пр.
1 Для f(z)
=
![]() точка z
= 0 устранимая
особая точка
точка z
= 0 устранимая
особая точка
f(z)
=
![]() (
z
-
(
z
-
![]() ) = 1 -
) = 1 -
![]()
Пр.2
Для f(z)
=
![]() точка z
= 0 - полюс
1 – ого порядка
точка z
= 0 - полюс
1 – ого порядка
f(z)
=
![]() (
z
-
(
z
-
![]() ) =
) =
![]() -
-
![]()
Пр. 3 Для f(z) = e1/z точка z = 0 - существенно особая точка
f(z)
= e1/z
=
![]()
Если
при z![]() a
lim
(z
– a)k
f(z)
= c
a
lim
(z
– a)k
f(z)
= c
![]() 0 , то z
= a
есть
полюс k
– ого порядка
для f(z).
0 , то z
= a
есть
полюс k
– ого порядка
для f(z).
Коэффициент А-1 полюса 1 – ого порядка наз. вычетом.
Пр. Разложить в ряд Тейлора по степеням (z – i) функцию f(z) = z5 .
Решение. f(z) = z5 , f(i) = I f’’’(z) = 60z2 , f’’’(i) = - 60
f’(z) = 5z4 , f’(i) = 5 f(4)(z) = 120z , f(4)(i) = 120i
f’’(z) = 20z3, f’’(z) =-20 i f(5)(z) = 120 , f(5)(z) = 120
f(6)(z) = 0
f(z) = i + 5(z – i) - 10i(z – i)2 - 10(z – i)3 + 5i(z – i)4 + (z – i)5
Рядом Тейлора функции f(z) = z5 является многочлен 5 степени.
Пр.
Разложить в ряд Тейлора по степеням z
– (1 -
![]() )функцию
f(z)
= ch(1 – z) .
)функцию
f(z)
= ch(1 – z) .
Решение.
f(z)
= ch(1 – z) f’(a) = ch(![]() )
= cos(
)
= cos(![]() )
= 0
)
= 0
f’(z)
= - sh(1 – z) f’(a) = - sh(![]() )
= -i sin(
)
= -i sin(![]() )
= -i
)
= -i
f’’(z) = ch(1 – z) f’(a) = 0
f’’’(z) = - sh(1 – z) f’(a) = -i
Остаются только нечетные степени разложения с общим множителем -i
f(z)
= -i
[ (z
– 1 +
![]() )
+
)
+
![]() (z
– 1 +
(z
– 1 +
![]() )3
+
)3
+
![]() (z
– 1 +
(z
– 1 +
![]() )5
+ . . . ]
)5
+ . . . ]
Пр. Исследовать сходимость ряда
.
. . +
![]() +
+
![]() +
+
![]() + 1 + (
+ 1 + (![]() )
+ (
)
+ (![]() )2
+ (
)2
+ (![]() )3
+ . . .
)3
+ . . .
Решение.
Это сумма двух геометрических прогрессий
с q1
=
![]() , q2
= (
, q2
= (![]() )
. Из условий
их сходимости следует
)
. Из условий
их сходимости следует
![]() < 1 ,
< 1 ,
![]() < 1 или
z
> 1 , z
< 2 , т.е.
область сходимости ряда кольцо 1
< |z|
< 2 .
< 1 или
z
> 1 , z
< 2 , т.е.
область сходимости ряда кольцо 1
< |z|
< 2 .
Пр.
Разложить по степеням z
в ряд Лорана функцию f(z)
=![]() в окрестности
z
= 0
в окрестности
z
= 0
Решение.
Представим функцию в виде f(z)
= - z2
![]() .Имеем сумму
геометрической прогрессии со знаменателем
q
= z
. В круге
|z|
< 1 она
сходится.
.Имеем сумму
геометрической прогрессии со знаменателем
q
= z
. В круге
|z|
< 1 она
сходится.
f(z) = - z2 ( 1 + z2 + z3 + z4 + . . . ) = - z2 - z3 - z4 - . . .
Пр.
Разложить по степеням z
в ряд Лорана функцию f(z)
=
![]() в кольце 1
< |z|
< 3 . Решение.
Разложим функцию на простейшие дроби
в кольце 1
< |z|
< 3 . Решение.
Разложим функцию на простейшие дроби
![]() =
=
![]() +
+![]() =
=![]() .Из условий
z
= 1
.Из условий
z
= 1
![]() A
= -1/2 , z
= 3
A
= -1/2 , z
= 3
![]() B
= ½ . С учетом
условия 1 <
|z|
< 3 запишем
f(z)
= -
B
= ½ . С учетом
условия 1 <
|z|
< 3 запишем
f(z)
= -![]()
![]() -
-![]()
![]() . Это суммы
геометрических прогрессий, которые
сходятся в кольце
. Это суммы
геометрических прогрессий, которые
сходятся в кольце
f(z)
= -
![]() (
(
![]() )
)
Для этой функции z = 0 существенно особая точка.
Теорема о вычетах.
Пусть f(z) аналитическая функция в области, ограниченной контуром L за исключением полюса в точке а . Тогда значение интеграла от f(z) по контуру L равно вычету в точке а .
![]() f(z)
dz
= 2
f(z)
dz
= 2![]() i
A-1
(
44
)
i
A-1
(
44
)
A-1
- коэффициент
при
![]() в разложении
f(z)
в ряд Лорана.
в разложении
f(z)
в ряд Лорана.
Док
– во. Если
а – полюс
порядка n
, то f(z)
=
![]() + . . . +
+ . . . +![]() +
+![]() (z),
(z),
где
правильная часть ряда Лорана
![]() (z)
- аналитическая
функция. Интеграл от неё по замкнутому
контуру равен 0 (теорема Коши).
(z)
- аналитическая
функция. Интеграл от неё по замкнутому
контуру равен 0 (теорема Коши).
![]()
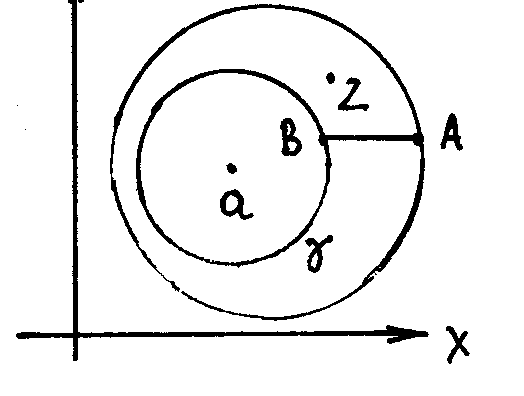 f(z)
dz
= A-n
f(z)
dz
= A-n
![]()
![]() + . . . +A-1
+ . . . +A-1
![]()
![]() +0
+0
Вокруг
точки а
опишем окружность
![]() радиусаr
и получим
кольцевую область, где функции
радиусаr
и получим
кольцевую область, где функции
![]() аналитические. Тогда интеграл по внешнему
контуруL+
можно
заменить на интеграл по внутреннему
контуру
аналитические. Тогда интеграл по внешнему
контуруL+
можно
заменить на интеграл по внутреннему
контуру
![]() +
( 39 ) и вычислить его.
+
( 39 ) и вычислить его.
Пусть
z
– a = r eit
, тогда
dz
= ir eit
, 0 < t < 2![]()
![]()
![]() =
i
=
i![]()
![]() = 2
= 2![]() i
i
![]()
![]() =
i
=
i![]()
![]() =
=![]()
![]() ei(k
– 1)t
dt =
ei(k
– 1)t
dt =![]()
![]() [cos(k–1)t
+ i sin(k-1)t ] dt = 0
[cos(k–1)t
+ i sin(k-1)t ] dt = 0
т.е.после
интегрирования в разложении функции в
ряд остается только одно слагаемое 2![]() i
A-1
= 2
i
A-1
= 2![]() i
res
f(а)
.
i
res
f(а)
.
Еси функция f(z) имеет в пределах контура L несколько полюсов a1 , a2 , . . . , am , то интеграл равен сумме вычетов
![]()
 f(z)
dz
= 2
f(z)
dz
= 2![]() i
i
![]()
![]() (
45
)
(
45
)
Контур
односвязной области L’
теперь включит m
окружностей
![]() i
вокруг
каждого полюса и m
разрезов.
В результате интеграл по L+
будет равен
сумме интегралов по
i
вокруг
каждого полюса и m
разрезов.
В результате интеграл по L+
будет равен
сумме интегралов по
![]() i+
.
i+
.
Вычисление вычетов.
Пусть
f(z)
имеет полюс
первого порядка. Тогда она представляется
в виде частного f(z)
=![]() и ряда Лорана
f(z)
=
и ряда Лорана
f(z)
=
![]() +
+![]() (z)
. Умножим
f(z)
на (z
– a)
и перейдем
к пределу z
(z)
. Умножим
f(z)
на (z
– a)
и перейдем
к пределу z
![]() a
a
lim
f(z)(z – a) = lim
![]() = A-1
(
46 )
= A-1
(
46 )
т.е.
вычет функции с полюсом первого порядка
в точке а
равен пределу
произведения функции на двучлен (z
– a)
при z
![]() a
.
a
.
При вычислении предела в ( 2.17 ) используем правило Лопиталя
lim
![]() = lim
= lim
![]() = lim
= lim
![]() =
=
![]() = res f(z)(
47 )
= res f(z)(
47 )
т.е. для определения вычета достаточно значение числителя функции в точке а разделить на значение производной от знаменателя в этой точке
Если f(z) имеет в точке а полюс порядка n, разложение этой функции в ряд Лорана умножим на (z – a)n
(z
– a)n
f(z) = A-n
+ A1-n(z
– a) + A2-n(z
– a)2
+ . . . +
A-1(z
– a)n-1
+ (z
– a)n![]() (z)
,
(z)
,
(n
– 1) раз
продифференцируем и получим (n
– 1)! А-1
+ [(z
– a)n![]() (z)](n
– 1) .
Переход к пределу z
(z)](n
– 1) .
Переход к пределу z![]() a
исключит
второе слагаемое и определит вычет
a
исключит
второе слагаемое и определит вычет
res
f(z)
=
![]() lim
lim
![]() (
49
)
(
49
)
Пр.
Найти вычеты функции f(z)
=
![]()
Решение. Полюсами являются точки z = 1 , z = 3
![]() =
=
![]() (z
– 1)
(z
– 1)
![]() =
=
![]()
![]() = - ½
= - ½
![]() =
=
![]() (z
– 3)
(z
– 3)
![]() =
=
![]()
![]() = 3/2
= 3/2
или по формуле ( 2.18 ) : g(z) = z , h(z) = (z – 1)(z – 3) , h’(z) = 2z – 4 , тогда
![]() =
=
![]() =
- ½ ;
=
- ½ ;
![]() =
=
![]() = 3/2
= 3/2
Пр.
Найти вычеты функции f(z)
=
![]()
Решение. Здесь z = 2 - полюс третьего порядка, тогда
![]() =
=
![]()
![]()
 =
=
![]()
![]()
![]() =
=
![]() 2
= 1
2
= 1
Вычисление интегралов.
Пусть
f(z)
аналитическая
функция в верхней полуплоскости, включая
действительную ось, за исключением n
полюсов ai
расположенных
над осью Ох. Кроме того lim
z2
f(z)
= C
– конечное
число при |z|![]() ,
т.е. на
бесконечности функция становится
двукратной нулевой точкой. Тогда
определенный интеграл
,
т.е. на
бесконечности функция становится
двукратной нулевой точкой. Тогда
определенный интеграл![]() f(x)dx
функции
действительной
переменной
равен
f(x)dx
функции
действительной
переменной
равен
![]() f(x)
dx
= 2
f(x)
dx
= 2![]() i
( r1
+ r2
+ . . . + rn
) (
50
)
i
( r1
+ r2
+ . . . + rn
) (
50
)
где
ri
- вычеты
функции f(z)
в ai
. (
2.20 ) – часть
интеграла по замкнутому контуру. Он
состоит из действительной оси и
полуокружности радиуса R![]() , интеграл вдоль которой равен нулю в
силу дополнительного условия.
, интеграл вдоль которой равен нулю в
силу дополнительного условия.
Пр.
Вычислить J
=
![]()
![]() .
.
Решение.
Функция f(x)
=
![]() аналитическая в верхней полуплоскости,
за исключением полюса 2 порядка в 2i.
Проверка
дополнительного условия при |z|
аналитическая в верхней полуплоскости,
за исключением полюса 2 порядка в 2i.
Проверка
дополнительного условия при |z|![]()
lim
z2f(z)
= lim
![]() =
lim
=
lim
![]() =
{ z
= r
eit
} = lim
=
{ z
= r
eit
} = lim
![]() =
0
=
0
т.е. конечное число. Вычисление вычета по ( 2.18 )
![]() =
=
![]()
![]()
![]() =
=
![]()
![]()
![]() =
=
![]()
![]() =
=
![]()
Ответ.
J
= 2![]() i
i
![]() =
2
=
2![]() i
(
i
(![]() )
=
)
=
![]()
Пр.
Вычислить J
=![]()
![]() ,
если
,
если![]() -окружности:1)|z|
= 1, 2)
|z|
= 3, 3)
|z|
= 5
-окружности:1)|z|
= 1, 2)
|z|
= 3, 3)
|z|
= 5
Решение. Найдем вычеты относительно полюсов z = 0 , z = - 2 , z = - 4
![]()
 =
=
![]() z
f(z)
=
z
f(z)
=
![]()
![]() = 1/8
= 1/8
![]() =
=
![]() (z
+ 2) f(z)
=
(z
+ 2) f(z)
=
![]()
![]() = - ¼
= - ¼
![]() =
=
![]() (z
+ 4) f(z)
=
(z
+ 4) f(z)
=
![]()
![]() = 1/8
= 1/8
1)
Внутри окружности |z|
= 1 находится
один полюс z
= 0
![]() J1
= 2
J1
= 2![]() i
(
i
(![]() )
=
)
=
![]() i
/ 4
i
/ 4
2)
Внутри окружности |z|
= 3 находятся
полюсы z
= 0, z
=-2
![]() J2
= 2
J2
= 2![]() i
(
i
(![]() )
= -
)
= -![]() i
/ 4
i
/ 4
3)
Внутри окружности |z|
= 5находятся
полюсы z
= 0, z
=-2, z
=-4![]() J3
= 2
J3
= 2![]() i(
i(![]() )=
0
)=
0
