7. Квантово-механическое описание атома водорода

7.1. Уравнение Шредингера для атома водорода. Главное квантовое число

Рассмотрим в качестве модельной простейшую систему, состоящую из неподвижного ядра с зарядом Z = 1 и одного электрона, т.е. атом водорода. Аналогичным образом будут описываться так называемые водородоподобные ионы, которые представляют собой электрон, движущийся вокруг ядра, имеющего заряд больше Z > 1.

Потенциальная энергия электрона в кулоновском поле ядра равна:

(7.1)

Таким образом, уравнение Шредингера принимает вид:

(7.2)

где r – расстояние электрона от ядра, m_e – масса электрона.

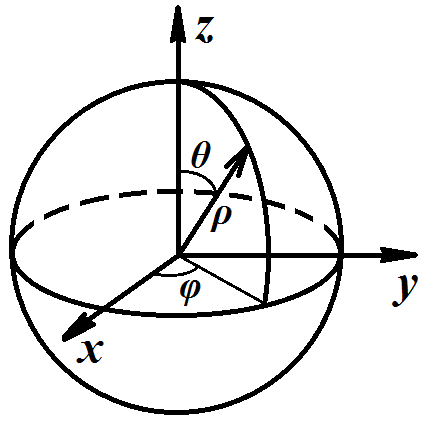
Рис. 7.1. Полярные координаты (ρ, φ, θ)

Наиболее просто уравнение решается в полярных координатах (рис. 7.1), так как поле, в котором движется электрон, является центрально-симметричным.

В полярных координатах (ρ, φ, θ) уравнение Шредингера имеет вид:

(7.3)

Можно показать, что это уравнение имеет решение при любых E > 0, а также в случае, если E принимает одно из дискретных отрицательных значений, равных: 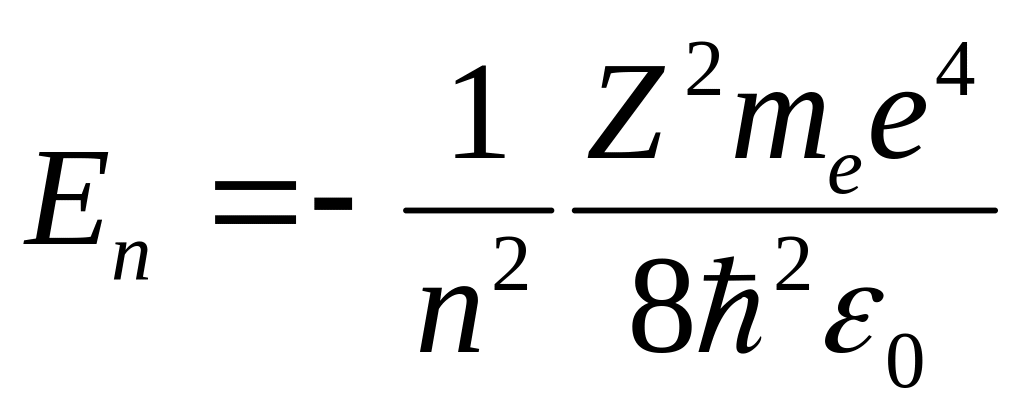(n = 1, 2, 3,...) (7.4)

Случай E > 0 соответствует электрону в свободном состоянии (рис. 7.2), то есть электрону, который пролетает вблизи ядра, а затем удаляется на бесконечность. Энергия электрона E < 0 означает, что он связан с ядром.

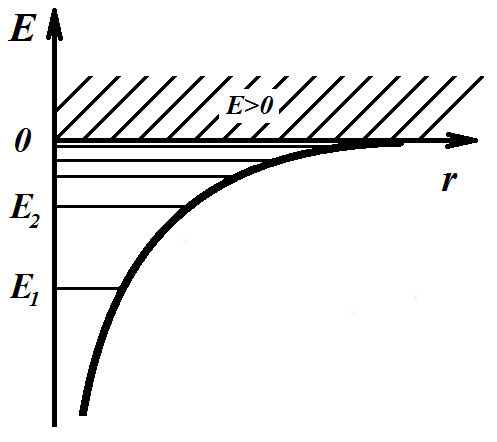
Рис. 7.2. Энергия электрона в атоме

Собственные функции уравнения (7.3) зависят от трех целочисленных параметров: n, l, m: (7.5)

Параметр n называют главным квантовым числом, он указывает номер энергетического уровня (см. раздел 5).

7.2. Момент импульса атома. Орбитальное и магнитное квантовые числа

Параметры l и m представляют собой азимутальное (или орбитальное) и магнитное квантовые числа. Поясним их появление. Рассмотрим стационарное уравнение Шредингера (в декартовых координатах):

(7.6)

Выражение справа представляет собой произведение волновой функции и параметра Е (который может быть равен одному из собственных значений). Выражение слева – это комбинация математических операций, действующих на волновую функцию. Эту комбинацию можно выписать отдельно, обозначив : (7.7)

Эту и множество других комбинаций математических функций в квантовой механике называют операторами. Выражение (7.7) называется оператором Гамильтона или Гамильтонианом. Гамильтониан является оператором энергии.

Тогда уравнение (7.6) можно переписать в виде:

(7.8)

Другим измеряемым величинам сопоставляются соответствующие операторы – координат, импульса, момента импульса и т.д. В каждом конкретном случае оператором является определенная комбинация математических функций, действие которых на волновую функцию позволяет найти собственные значения искомой величины (координаты, импульса и т.д.). Эти собственные значения данной физической величины, и только они, могут быть получены экспериментальным путем, то есть являются реальными значениями данной величины.

Аналогично, как решение уравнения Шредингера позволяет найти возможные значения энергии, нахождение возможных значений любых других величин сводится к решению соответствующих операторных уравнений.

Напомним, что механический момент импульса (орбитальный момент) материальной точки, вращающейся вокруг неподвижной оси, можно найти по формуле: (7.9)

где – радиус-вектор точки на орбите, – вектор импульса точки.

Учитывая особенности движения квантовых частиц, искать момент импульса атома по формуле (7.9) нельзя. Необходимо вводить соответствующий оператор и решать операторное уравнение. В частности, для момента импульса в квантовой механике вводят четыре оператора:

квадрат момента импульса;

, , – проекции момента импульса на координатные оси.

Нахождение возможных значений квадрата момента импульса сводится к решению уравнения , что является довольно трудной задачей. Ограничимся приведением конечного результата:

(7.8’)

Соответственно модуль момента импульса M равен:

(l = 0, 1, 2,..., n – 1) (7.9’)

где l - азимутальное или орбитальное квантовое число, упомянутое выше.

На рис. 7.3 изображены векторы M для двух орбитальных квантовых чисел (l = 1 и l = 2). Видно, что при увеличении числа l модуль орбитального момента импульса увеличивается согласно формуле (7.9’) – на рисунке для различных l все возможные векторы M являются радиусами одной сферы.

Это не означает, что электрон движется по какой-то орбите радиуса r = M. Сфера лишь подчеркивает, что куда бы ни был направлен вектор орбитального момента, его модуль будет равен при данном значении орбитального квантового числа l. При этом орбитальный момент импульса электрона M может иметь лишь такие ориентации в пространстве (рис. 7.3), при которых проекция M_z вектора M на направление внешнего магнитного поля принимает только квантованные значения, кратные ħ (направление оси z задаем вдоль направления внешнего магнитного поля).

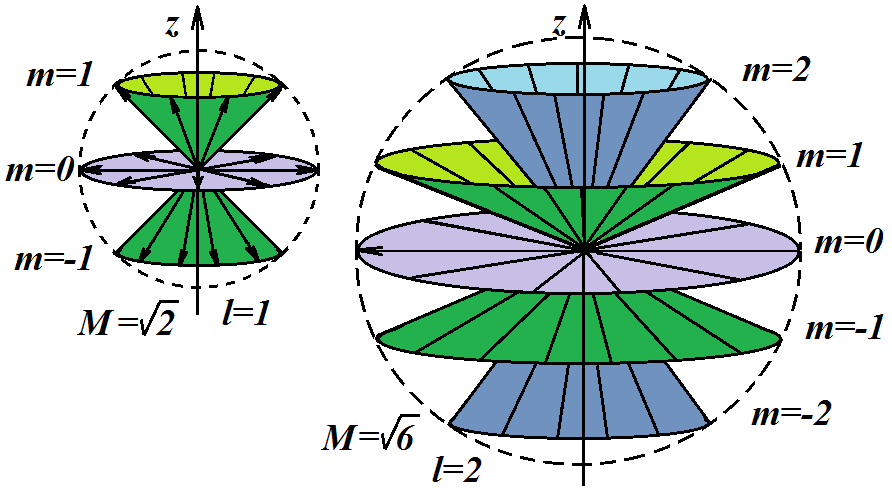
Рис. 7.3. Пространственное квантование момента импульса электрона

Это правило, называемое «пространственным квантованием», отражает суть особого свойства момента импульса микрочастицы – он может принимать только строго определенные значения и иметь только строго определенные направления в пространстве.

Итак, второе квантовое число, называемое орбитальным, возникает при нахождении возможных значений квадрата момента импульса; определяет величину (модуль) момента импульса (механического орбитального момента) электрона в атоме.

Найти возможные направления момента импульса можно, вычислив проекцию орбитального момента на заданную ось. Проекция M_z на некоторое направление z будет определяться из операторного уравнения:

(7.10)

его решение имеет вид:

(m_l = 0, ±1, ±2,..., ±l) (7.11)

где m_l – магнитное квантовое число (в формуле (7.5) и на рисунке 7.3 обозначено m).

Третье квантовое число, называемое магнитным, возникает при нахождении возможных значений проекции момента импульса на выделенную ось; определяет проекцию момента импульса электрона на заданное направление.

На рис. 7.3 приведены возможные ориентации векторов M: для электронов с l = 1 число возможных ориентаций равно 3 – под углом вверх, вниз и перпендикулярно оси z; для l = 2 число возможных ориентаций соответственно равно 5, и т.д. Таким образом, вектор M может принимать (2l + 1) ориентаций в пространстве. Каждый конус на рисунке соответствует одному из возможных направлений вектора M, при этом высота конуса равна m_lħ: для m_l = 0 конус вырождается в диск, для m_l = 1 высота конуса равна ħ и т.д.

Итак, каждому собственному значению E_n (кроме E₁, которому соответствует одна собственная функция ψ₁₀₀) соответствует несколько собственных функций ψ_nlm, отличающихся значениями орбитального n и магнитного m_l квантовых чисел. Это означает, что атом может иметь одно и то же значение энергии, находясь в различных состояниях. Эти состояния называют вырожденными, а число состояний, соответствующих одному собственному значению E_n, называется кратностью вырождения. Например,

для n = 2 возможны значения l: 0 и 1;

для l = 0 возможно единственное значение m_l = 0,

для l = 1 возможны 3 значения m_l = –1, 0 и 1.

Итого: для Е₂ возможны 4 состояния с различными комбинациями l и m_l.

Забегая вперед, скажем, что существует еще одно квантовое число, принимающее два возможных значения. С учетом этого квантового числа для Е₂ возможно 8 состояний, или другими словами, в одном атоме могут находится 8 электронов в различных состояниях с энергией Е₂.